（笔记）交互题 构造题

交互题分为IO交互和交互库函数交互。

这类题通常有一定的操作次数限制，要求你构造出一种解来猜出答案。

怎么做交互题？可以的方法是首先观察操作次数限制，以此可以大概确定操作是 \(O(n\log n),O(\log n),O(n)\) 等级别中的哪一个并且猜一个做法。

有些交互题是假交互题，仅仅是为了交互而交互，事实上去掉这个功能直接用 IO 对题目没有任何影响。

交互库函数交互

编码方法

以P1947 猜数为例，题目要求编写一个实现函数int Chtholly(int n,int c)，可以调用的程序需要事先声明。

#include<bits/stdc++.h>
extern "C" int Seniorious(int x);
extern "C" int Chtholly(int n,int c){
	int l=1,r=n;
	while(l<r){
		int mid=(l+r)>>1;
		int ret=Seniorious(mid);
		if(ret==0)return mid;
		else if(ret==1)r=mid-1;
		else l=mid+1;
	}
	return l;
}

其中extern "C"的作用是方便本地调试，即 C++ 编译器会把函数名映射到另一个名字上进行编译，extern "C"就是强迫用同一个名字进行编译，这样后续调试才能和交互库的函数名吻合。

接下来是调试部分：

  1. 使用 cmd，先调出命令提示符，输入盘符（如D:），然后输入cd D:\GD1145\cpp（代码目录）。

  2. 使用 Powershell，按住shift再在文件夹空白处右键打开 Powershell 即可。

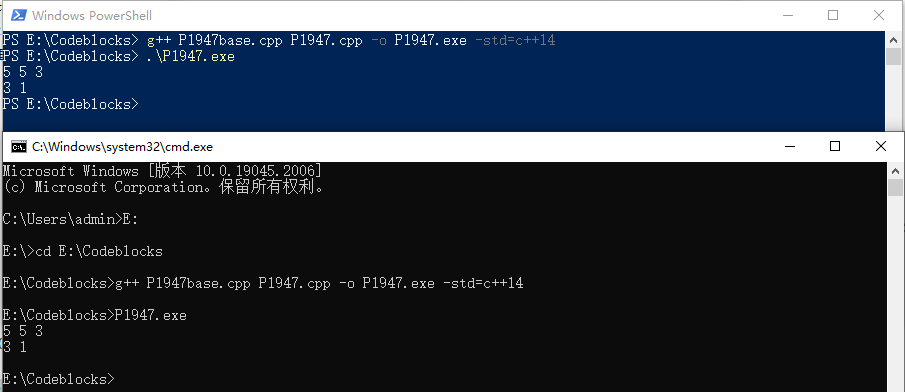
注意：这里你应该先把两个文件保存至同一目录下，然后如果你用的是 Dev-C++ 就把你的编译器 MinGW64 的 bin 目录加入系统环境变量的 Path。

不妨另交互库为lib.cpp，选手代码为my.cpp，那么应该在接下来输入g++ lib.cpp my.cpp -o my.exe -std=c++14。接下来的调试，在 cmd 输入my.exe 然后输入相应数据即可。在 Powershell 中，输入.\my.exe然后是一样的。

经过验证，编译命令中文件名先后顺序不重要。

image

P5875 [IOI 2014] friend 朋友

没有找到这题的交互库附件。

考虑时光倒流，分类讨论。为什么不能正着处理呢？原因是前面的操作对后面有后效性，而后面对前面是没有影响的。

  1. 两点 \(i,j\) 直接连边，即只能选一个，反悔贪心地我们先把答案加上 \(a_i\)，然后 \(a_j\leftarrow max(a_j-a_i,0)\)。

  2. \(i\) 与 \(j\) 的所有邻居连边，两者要么就都不选，要么就都选，所以直接推到选 \(j\) 的时候再说即可，\(a_j\leftarrow a_j+a_i\)。

  3. \(i\) 与 \(j\) 与其所有邻居连边，那么 \(a_j\leftarrow max(a_j,a_i)\)。

当然，如果你的代码惯用std功能，需要加上using namespace std;。请注意！如果题面明确指出extern "C"的使用与否，请严格遵循其交互指示。

#include<bits/stdc++.h>
using namespace std;
int findSample(int n, int a[], int b[], int c[]){
	b[0]=0;
	for(int i=n-1;i>0;i--){
		int j=b[i];
		if(c[i]==0)b[0]+=a[i],a[j]=max(0,a[j]-a[i]);
		else if(c[i]==1)a[j]+=a[i];
		else a[j]=max(a[j],a[i]);
	}
	return b[0]+a[0];
}

P6612 [POI 2012] LIC-Bidding

本题是一道博弈论DP的经典题目。通过最优解可实现的时间复杂度为 \(O(n\log_2n\log_3n)\) 一次操作。

具体来说，令 \(f_{i,j,k}\) 表示当前 \((x,y)\) 中 \(y=i\)，\(x=2^j\times 3^k\) 的选择操作（\(0\) 表示必败态，这可能在 Nim 游戏及其扩展结论中有较多应用），然后进行转移。

\[\begin{aligned} f_{i,j,k}=\begin{cases}0 &2^j\times 3^k\geq n \\1 &f_{i+2^j\times 3^k,0,0}=0 \\2 &f_{i,j+1,k}=0 \\3 &f_{i,j,k+1}=0 \\0 &\text{otherwise} \end{cases} \end{aligned} \]

#include<bits/stdc++.h>
using namespace std;
const int N=3e4+5;
int f[N][22][12],p2[22],p3[12];
bool tag=0;
extern "C" int _opt(int n,int x,int y){
	if(!tag){
		tag=1;
		int lim2=0,lim3=0;
		p2[0]=p3[0]=1;
		for(int i=1;i<=n;i*=2)
			lim2++,p2[lim2]=i*2;
		for(int i=1;i<=n;i*=3)
			lim3++,p3[lim3]=i*3;
		for(int i=n;i>=0;i--)
			for(int j=lim2;j>=0;j--)
				for(int k=lim3;k>=0;k--){
					if(i+p2[j]*p3[k]>=n)f[i][j][k]=0;
					else {
						if(!f[i][j+1][k])f[i][j][k]=2;
						else if(!f[i][j][k+1])f[i][j][k]=3;
						else if(!f[i+p2[j]*p3[k]][0][0])f[i][j][k]=1;
						else f[i][j][k]=0;
					}
				}
	}
	if(x+y>=n)return 1;
	int cn2=0,cn3=0;
	while(x%2==0&&x>0)cn2++,x/=2;
	while(x%3==0&&x>0)cn3++,x/=3;
	return f[y][cn2][cn3];
}

很诡异的教训，非运算符优先级一定要注意，一开始写成!x%2&&x>0获得了若干个 RE，然后发现不能这么判，得加多几个括号或者直接写==0。

正确示范：

while(!(x%2)&&x>0)

IO交互

对于IO交互，每次操作都要清空缓存区：

  • 对于 C/C++：fflush(stdout)；
  • 对于 C++：std::cout << std::flush；
  • 对于 Java：System.out.flush()；
  • 对于 Python：stdout.flush()；
  • 对于 Pascal：flush(output)；
  • 对于其他语言，请自行查阅对应语言的帮助文档。

P1733 猜数（IO交互版）

二分即可。需要注意的是除了fflush(stdout)，还可以采用std::endl的方式清空缓存区。

P8849 『JROI-7』hibernal

主要是分组的思想。考虑到我们无论怎么样分组在随机数据下都是等效的，所以不妨让分组先在值域上连续。考虑需要分别分出两个单独包含苹果的 \(S_1,S_2\)，则对于每个集合，如果询问的区间 \([l,r]\) 中包含苹果，那么返回值肯定是 \(1\)，因为另一个集合必定会有一个苹果，这样就可以在 \(\lceil \log n\rceil-1\) 的操作内找到一个苹果。如何分出这两个集合呢？考虑二进制分组！（请记住这种典型 trick），如果返回 \(1\) 说明两个苹果在该位上二进制不同。找任意一个返回为 \(1\) 的划分 \(S_1,S_2\)，然后找到一个苹果位置，另一个直接异或即可。

#include<bits/stdc++.h>
using namespace std;
const int N=1024;
int T,n,rm;
int cnt,a[N];
int main(){
	fflush(stdout);
	scanf("%d",&T);
	while(T--){
		fflush(stdout);
		scanf("%d",&n);
		int val=0;
		cnt=0;
		for(int i=0;(1<<i)<=n;i++){
			printf("? ");
			int cnv=0;
			for(int j=1;j<=n;j++)
				if((1<<i)&j)cnv++;
			printf("%d ",cnv);
			for(int j=1;j<=n;j++)
				if((1<<i)&j)printf("%d ",j);
			printf("\n");
			fflush(stdout);
			int ret;scanf("%d",&ret);
			if(ret){rm=i;val|=(1<<i);}
		}
		for(int i=1;i<=n;i++)
			if((1<<rm)&i)a[++cnt]=i;
		int l=1,r=cnt;
		while(l<r){
			int mid=(l+r)>>1;
			printf("? %d ",mid-l+1);
			for(int i=l;i<=mid;i++)
				printf("%d ",a[i]);
			printf("\n");
			fflush(stdout);
			int ret;scanf("%d",&ret);
			if(ret)r=mid;
			else l=mid+1;
		}
		int x=a[l],y=x^val;
		if(x>y)swap(x,y);
		printf("! %d %d\n",x,y);
		fflush(stdout);
	}
	return 0;
}

CF835E The penguin's game

和上一题一样，只需要稍微改一点东西，如果返回值即不是 \(x\) 也不是 \(0\)，那么询问集合中就必然有 \(y\)。

#include<bits/stdc++.h>
using namespace std;
const int N=1024;
int n,rm,x,y;
int cnt,a[N];
int main(){
	fflush(stdout);
	scanf("%d%d%d",&n,&x,&y);
	int val=0;
	cnt=0;
	for(int i=0;(1<<i)<=n;i++){
		printf("? ");
		int cnv=0;
		for(int j=1;j<=n;j++)
			if((1<<i)&j)cnv++;
		printf("%d ",cnv);
		for(int j=1;j<=n;j++)
			if((1<<i)&j)printf("%d ",j);
		printf("\n");
		fflush(stdout);
		int ret;scanf("%d",&ret);
		if(ret!=x&&ret!=0){rm=i;val|=(1<<i);}
	}
	for(int i=1;i<=n;i++)
		if((1<<rm)&i)a[++cnt]=i;
	int l=1,r=cnt;
	while(l<r){
		int mid=(l+r)>>1;
		printf("? %d ",mid-l+1);
		for(int i=l;i<=mid;i++)
			printf("%d ",a[i]);
		printf("\n");
		fflush(stdout);
		int ret;scanf("%d",&ret);
		if(ret!=x&&ret!=0)r=mid;
		else l=mid+1;
	}
	int x=a[l],y=x^val;
	if(x>y)swap(x,y);
	printf("! %d %d\n",x,y);
	fflush(stdout);
	return 0;
}

构造题

构造题种类形式常常多种多样，但是交互题一定离不开构造的思想。

CF2096G Wonderful Guessing Game

在本题中我们掌握一个较为重要的结构决策树。

先考虑没有一次性询问和忽略操作的情况。

利用题目的操作特性，我们不难想到小学数学问题找次品的问题。具体来说，对于区间 \([L,R]\)，如果长度整除 \(3\) 分成三等分，从左到右依次标号为 \(0\) 到 \(2\)。如果余 \(1\) 塞到最后一份，如果余 \(2\) 塞到前面两份。总之就是要保证 \(0\) 和 \(1\) 的长度相等。如 \([1,8]\) 分成 \([1,3],[4,6],[7,8]\)，\([1,7]\) 分成 \([1,2],[3,4],[5,7]\)，\([1,6]\) 分成 \([1,2],[3,4],[5,6]\)。

这里的分区间有一个细节，当一个区间 \([l,r]\) 长度为 \(1\) 但是深度还没有达到最大值时，需要不断地加入它的 \(2\) 儿子直到到达最深区间为止（如上图 \(5\)），这是因为要保证每个节点都要跳 \(mxdep\) 次才能到达。考虑如果不这么做的话，如果答案叶子结点不在最下层，而我们一开始记录的 \(X\) 就会包括后面的若干个N，它们对 \(X\) 的贡献都是 \(2\)，这样会对答案造成极大的干扰。

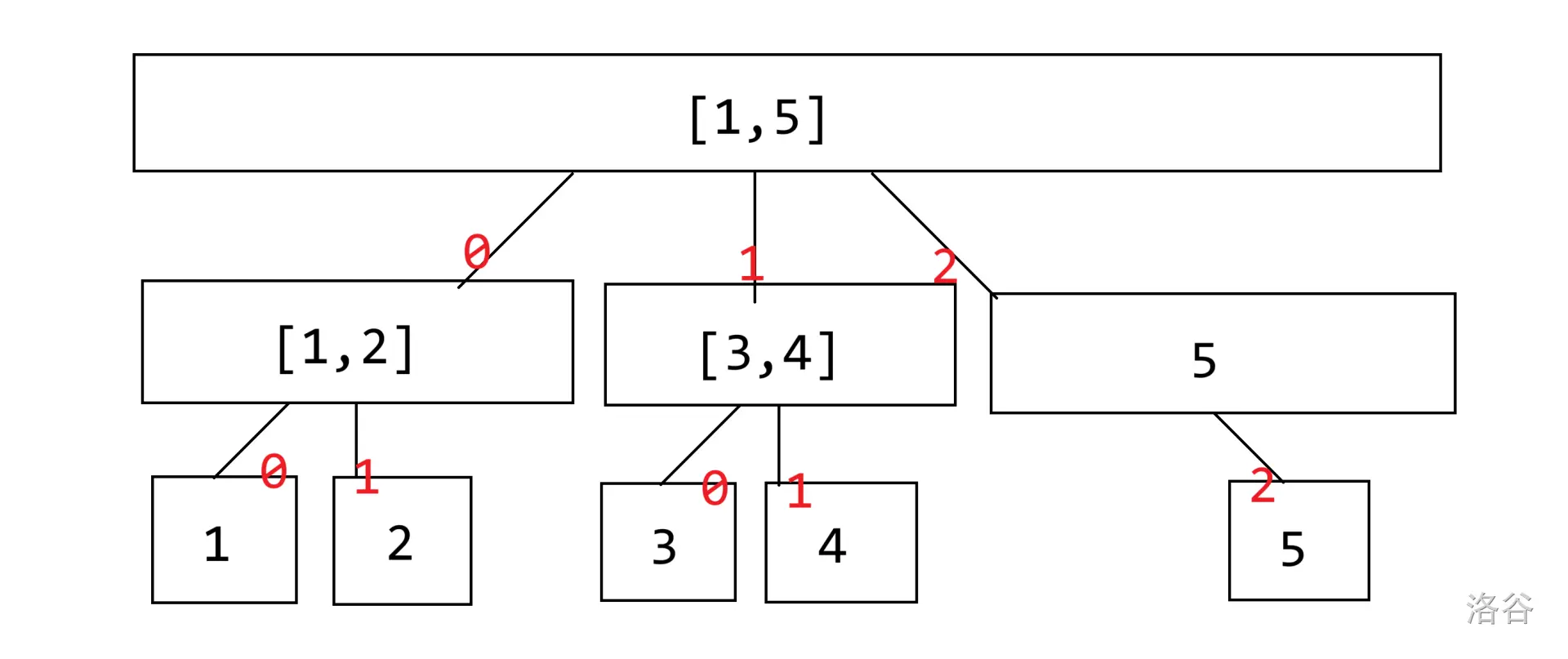
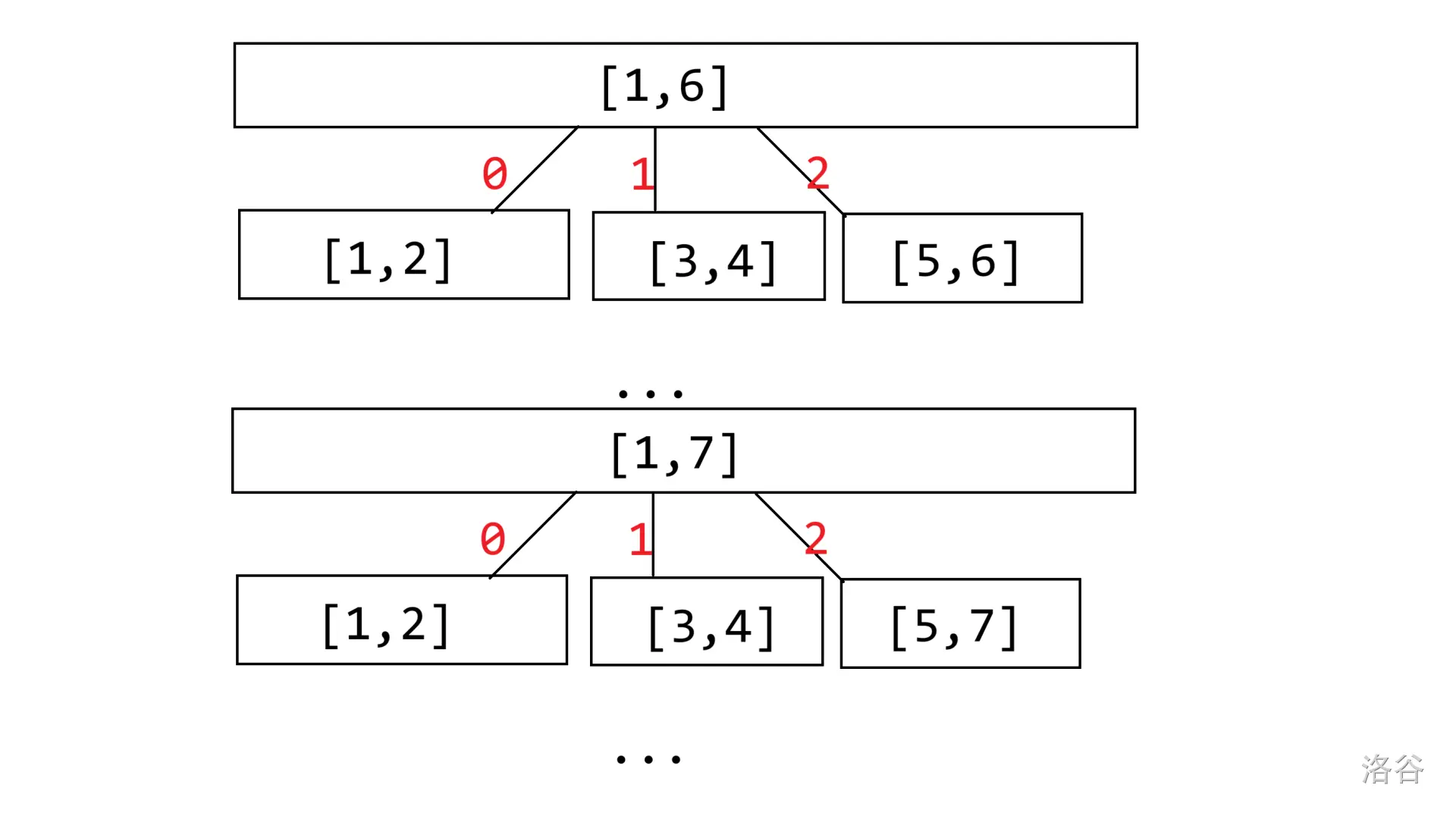
image

image

（图片来自题解区@maxiaomeng，侵删）

这样下来总操作数就可以达到 \(\lceil \log_3 n\rceil\) 的。

考虑单次操作，只需要询问当前决策点中 \(0\) 和 \(1\) 拼起来的区间，如果返回 L 说明在 \(0\)，R 说明在 \(1\)，N 说明在 \(2\)。考虑一次性弄完这些操作，这时候我们只需要把整个决策层的左右 \(0\) 区间先拼起来记为 \(M_0\)，\(1\) 区间先拼起来记为 \(M_1\)，容易知道它们的长度是相等的。然后在把 \(M_0,M_1\) 拼起来，一次性询问一层而不是仅仅一个决策点。这样我们就可以得到每一层的走向。

最后考虑被忽略的查询，这很人类智慧，看了好久才懂。我们观察到最终的决策树走向可以写成一个三进制数的形式（形如 \(01212X1\)，其中 \(X\) 是被忽略的询问，令 \(sum\) 为除 \(X\) 的所有数位上的数和）。这样我们只需要对于决策树上的每个叶子结点都记下它到根节点的边权和，对 \(3\) 取模，然后放在对应新区间里。总共会分成三个区间，这三个区间再加一个查询操作会返回一个 \(Y\)，这样我们就知道最终答案所在叶子结点到根节点的边权和为 \(Y\)，与 \(X\) 作差就可以得到缺少的那个决策层是往哪里走的。

关于为什么这样构造补充查询可以得到至少两种编号数量相同，有一个严谨的证明，请移步原作者题解：CF2096G Wonderful Guessing Game。

代码写得比较史，加入了很多不必要的码量，仅供参考。

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int n,root,ncnt,mxdep;
int rcd[N],deps[N];
vector<int>P[3];
struct Node{int ch[3],l,r;}t[N*5];
vector<int>G[20][3];
int build(int l,int r,int dep,int sum){
	t[++ncnt].l=l;
	t[ncnt].r=r;
	int u=ncnt;
	if(l==r){
		if(dep!=mxdep)t[u].ch[2]=build(l,r,dep+1,(sum+2)%3),G[dep+1][2].push_back(l);
		else P[sum].push_back(l);
		return u;
	}
	int siz=r-l+1;
	if(siz==2){
		t[u].ch[0]=build(l,l,dep+1,sum);
		G[dep+1][0].push_back(l);
		t[u].ch[1]=build(r,r,dep+1,(sum+1)%3);
		G[dep+1][1].push_back(r);
		return u;
	}
	if(siz%3==0||siz%3==1){
		t[u].ch[0]=build(l,l+siz/3-1,dep+1,sum);
		for(int i=l;i<=l+siz/3-1;i++)G[dep+1][0].push_back(i);
		t[u].ch[1]=build(l+siz/3,l+siz/3*2-1,dep+1,(sum+1)%3);
		for(int i=l+siz/3;i<=l+siz/3*2-1;i++)G[dep+1][1].push_back(i);
		t[u].ch[2]=build(l+siz/3*2,r,dep+1,(sum+2)%3);
		for(int i=l+siz/3*2;i<=r;i++)G[dep+1][2].push_back(i);
	}
	else {
		t[u].ch[0]=build(l,l+siz/3,dep+1,sum);
		for(int i=l;i<=l+siz/3;i++)G[dep+1][0].push_back(i);
		t[u].ch[1]=build(l+siz/3+1,l+siz/3*2+1,dep+1,(sum+1)%3);
		for(int i=l+siz/3+1;i<=l+siz/3*2+1;i++)G[dep+1][1].push_back(i);
		t[u].ch[2]=build(l+siz/3*2+2,r,dep+1,(sum+2)%3);
		for(int i=l+siz/3*2+2;i<=r;i++)G[dep+1][2].push_back(i);
	}
	return u;
}
int tonum(char x){
	if(x=='L')return 0;
	if(x=='R')return 1;
	return 2;
}
char tochar(int x){
	if(x==0)return 'L';
	if(x==1)return 'R';
	return 'N';
}
char opt[N];
int main(){
	int Tn;
	fflush(stdout);
	scanf("%d",&Tn);
	while(Tn--){
		fflush(stdout);
		ncnt=0;mxdep=0;
		scanf("%d",&n);
		for(int i=1;i<=19;i++)
			for(int j=0;j<3;j++)
				G[i][j].clear();
		for(int i=0;i<3;i++)P[i].clear();
		for(int i=1;i<n;i*=3)mxdep++;
		root=build(1,n,0,0);
		printf("%d\n",mxdep+1);
		for(int i=1;i<=mxdep;i++){
			printf("%d ",G[i][0].size()+G[i][1].size());
			for(int v:G[i][0])printf("%d ",v);
			for(int v:G[i][1])printf("%d ",v);
			printf("\n");
		}
		if(P[0].size()==P[1].size()){
			printf("%d ",P[0].size()+P[1].size());
			for(int v:P[0])printf("%d ",v);
			for(int v:P[1])printf("%d ",v);
			printf("\n");
		}
		else if(P[0].size()==P[2].size()){
			printf("%d ",P[0].size()+P[2].size());
			for(int v:P[0])printf("%d ",v);
			for(int v:P[2])printf("%d ",v);
			printf("\n");
		}
		else {
			printf("%d ",P[1].size()+P[2].size());
			for(int v:P[1])printf("%d ",v);
			for(int v:P[2])printf("%d ",v);
			printf("\n");
		}
		fflush(stdout);
		scanf("%s",opt+1);
		int id=0,tsum=0;
		for(int i=1;i<=mxdep;i++){
			if(opt[i]=='?')id=i;
			else tsum+=tonum(opt[i]);
		}
		tsum%=3;
		if(id){
			int z=0;
			if(P[0].size()==P[1].size()){
				if(opt[mxdep+1]=='L')z=0;
				else if(opt[mxdep+1]=='R')z=1;
				else z=2;
			}
			else if(P[0].size()==P[2].size()){
				if(opt[mxdep+1]=='L')z=0;
				else if(opt[mxdep+1]=='R')z=2;
				else z=1;
			}
			else {
				if(opt[mxdep+1]=='L')z=1;
				else if(opt[mxdep+1]=='R')z=2;
				else z=0;
			}
			opt[id]=tochar((z-tsum+3)%3);
		}
		int u=root;
		for(int i=1;i<=mxdep;i++)
			u=t[u].ch[tonum(opt[i])];
		printf("%d\n",t[u].l);
		fflush(stdout);
	}
	return 0;
}
posted @ 2025-05-19 21:52  TBSF_0207  阅读(29)  评论(0)    收藏  举报