题解：P6118 [JOI 2019 Final] 独特的城市 / Unique Cities

看题解没看太懂，遂写一篇细说一下在信息转移中的感悟。

一个结论

一个点 \(y\) 对于一个点 \(x\) 深度唯一，当且仅当点 \(y\) 在点 \(x\) 为根的树（注意！不是子树）的最长链上。一个点的最长链必然是它与直径两个端点之一的路径。为什么？考虑一条直径 \(AB\)，一个节点 \(u\) 和 \(u\) 在直径上距离最小的点 \(v\)。根据直径的定义，\(v\rightarrow A\) 和 \(v\rightarrow B\) 中必定是关于 \(v\) 的最长链和次长链，否则一定可以找到更优的链作为直径的两半。由此可知命题成立。

一个做法

考虑分别以 \(A,B\) 进行 dfs，关于所有点的特殊点就只可能在它们到祖先的路径上。考虑动态维护这些点，用一个栈即可，再加上一个统计颜色的桶与一个维护多少个桶有值的变量。每个点 dfs 时维护以它为根的子树中的最长链和次长链。这里其实就默认了当前节点到祖先的链是最长链，维护的两个东西只能说是次长链（\(mxdep_u\)，表示绝对深度，下同）和次次长链（\(cdep_u\)，但是这其实是不严谨的，只是一种假想）。然后对于节点 \(u\)，\(dep_u\) 是到根的节点数即绝对距离，显然统计答案的时候需要把祖先中与之相距 \(\le mxdep_u-dep_u\) 的删掉。

为什么我们要先遍历长儿子再遍历其他？

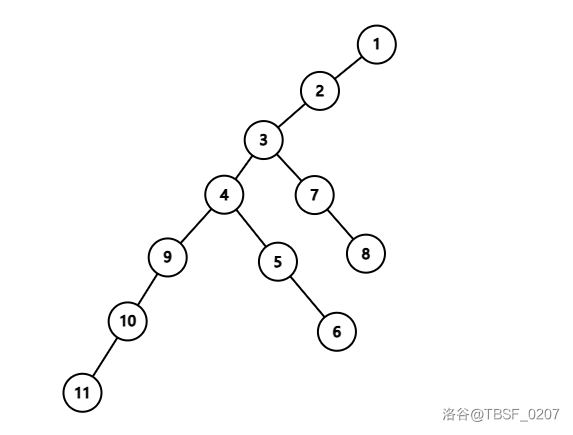
（在该图中，我们遍历到节点 \(3\)，长儿子是 \(4\)）

考虑到对儿子的影响，我们不能直接删掉所有 \(\le mxdep_u-dep_u\) 的节点。如果对于下一个遍历的节点，如果它是长儿子的话，要考虑的就是所有轻链与到祖先路径上深度重合的点。反之，要考虑的就是除去本条的所有轻链加上重链中与根节点路径上深度重合的点。总之你要想象把求答案的那个节点 \(u\) 提成绝对树根，然后假定祖先路径是绝对最长链。

考虑到这些路径与根节点的深度重合节点其实本质上只需要找出这些路径中的最长链，然后对祖先路径进行去重即可。明显我们要除去的 \(\le\) 次长链的限制比 \(\le\) 最长链的限制一定要小，是一个被包含的关系。所以我们采用这样的计算答案方式，先遍历长儿子再遍历其他，这样删的东西就是递进的而不用加东西回来。

这样我们就得到了一个 \(O(n)\) 做法。总结起来，先预处理直径的两个端点（代码里用的是两次 dfs），再分别以这两个端点为根进行 dfs，就像其他题解说的一样，每次进行如下操作：

1. 加入父节点。
2. 删掉祖先路径上距离 \(\le\) 次长链的节点。
3. 遍历长儿子。
4. 删掉祖先路径上距离 \(\le\) 最长链的节点。
5. 统计答案
6. 遍历其他儿子。
7. 删掉父节点。

再补充一点东西，这是原洛谷题解里面没有的。如何保证无后效性？对于同级的儿子节点，显然当我们采用如上策略时不会相互影响。儿子对父亲呢？考虑节点的加入，由于 dfs 末尾一定会删掉父节点，所以不用担心多算答案。会不会多删答案呢？由于 \(mxdep_v\le mxdep_u,dep_v=dep_u+1\implies mxdep_u-dep_u-1\geq mxdep_v-dep_v\)，每个节点的最终删答案一定是栈中所有的距离 \(\le mxdep_x-dep_x\) 的节点，所以势必不会影响到祖先的答案。

具体实现如下：

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int n,m,c[N],ans[N];
vector<int>G[N];
int st,en,dep[N];
int mxdep[N],cdep[N],son[N];
void dfs0(int u,int fa){
	dep[u]=dep[fa]+1;
	if(dep[u]>dep[en])en=u;
	for(int v:G[u]){
		if(v==fa)continue;
		dfs0(v,u);
	}
}
void merge(int x,int y){
	if(mxdep[y]>mxdep[x])cdep[x]=mxdep[x],mxdep[x]=mxdep[y],son[x]=y;
	else if(mxdep[y]>cdep[x])cdep[x]=mxdep[y];
}
void dfs1(int u,int fa){
	dep[u]=dep[fa]+1;
	mxdep[u]=cdep[u]=0;
	son[u]=0;
	for(int v:G[u]){
		if(v==fa)continue;
		dfs1(v,u);
		merge(u,v);
	}
	if(!son[u])mxdep[u]=dep[u];
}
int stk[N],tp,buk[N],ext;
void add(int &u){
	buk[c[u]]++;
	if(buk[c[u]]==1)ext++;
}
void del(int &u){
	buk[c[u]]--;
	if(!buk[c[u]])ext--;
}
void dfs3(int u,int fa){
	if(fa)add(stk[++tp]=fa);
	while(tp&&dep[u]-dep[stk[tp]]<=cdep[u]-dep[u])del(stk[tp--]);
	if(son[u])dfs3(son[u],u);
	while(tp&&dep[u]-dep[stk[tp]]<=mxdep[u]-dep[u])del(stk[tp--]);
	ans[u]=max(ans[u],ext);
	for(int v:G[u]){
		if(v==fa||v==son[u])continue;
		dfs3(v,u);
	}
	if(tp&&stk[tp]==fa)del(stk[tp--]);
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<n;i++){
		int u,v;scanf("%d%d",&u,&v);
		G[u].push_back(v);
		G[v].push_back(u);
	}
	for(int i=1;i<=n;i++)
		scanf("%d",&c[i]);
	st=1,en=0;dfs0(st,0);
	st=en,en=0;dfs0(st,0);
	dfs1(st,0);dfs3(st,0);
	dfs1(en,0);dfs3(en,0);
	for(int i=1;i<=n;i++)printf("%d\n",ans[i]);
	return 0;
}