（笔记）笛卡尔树

前言：对着模板手敲笛卡尔树板子，这还真是写奇奇怪怪 DS 以来第一次没看别人的板子敲出来的。

笛卡尔树 Cartesian Tree

用法大概有在树上 DP，利用二叉树先序、中序、后序遍历等，一般都和区间最大值/最小值有关。

笛卡尔树的性质（小根堆为例）：在笛卡尔树上两个节点 \(u,v\)，\(\min_{i=u}^v pri[i]=pri[\text{LCA}(u,v)]\)。

问题背景

给定一个 \(1 \sim n\) 的排列 \(p\)，构建其笛卡尔树。

即构建一棵二叉树，满足：

  1. 每个节点的编号（键值 \(key\)）满足二叉搜索树的性质。

  2. 节点 \(i\) 的权值为 \(pri[i]\)，每个节点的权值满足小根堆（或大根堆）的性质。

二叉搜索树性质：对于任意节点 \(u\) 的左子树内节点 \(v_1\) 有 \(key[v_1]\le key[u]\)，右子树内节点 \(v_2\) 有 \(key[u]\le key[v_2]\)。

小根堆性质：对于任意节点 \(u\) 及其左右儿子 \(ls,rs\) 有 \(pri[u]\le pri[ls],pri[u]\le pri[rs]\)。

说白了就是静态平衡树（Treap）。

构建过程

构建一颗笛卡尔树的方式有很多种，然而最常用且最便捷的仍是 \(O(n)\) 的单调栈建树，这里以小根堆为例展示。

为便于表述，先给出下文用到的几个定义：

左父亲：一个节点的左父亲存在当且仅当该节点为父节点的右儿子。

右父亲：一个节点的右父亲存在当且仅当该节点为父节点的左儿子。

右链：一个集合，包含从根节点的右儿子与集合中点所有的右儿子，没有右儿子即不计入。

笛卡尔树有一个很奇妙的性质，你可以从一个叶子节点出发，每向上走一个节点相当于给区间向左或向右扩展了一定距离，并且如果走到的是右父亲，就是向右扩展，反之相同。

由这个性质我们可以得出，假如一个节点 \(v\) 代表区间 \([l,r]\)，向上走到的第一个左父亲一定是 \(l-1\)，走到的第一个右父亲一定是 \(r+1\)。

节点表示为 \(v\)，其权值表示为 \(val_v\)，其左儿子 \(ls\)，右儿子 \(rs\)，则显然有：

\(val_v\le val_{ls},val_v\le val_{rs}\)

\(ls<v,v<rs\)

建树过程加入第 \(i\) 个节点，可以假设已经加好了前 \(i-1\) 个节点，此时利用单调栈维护笛卡尔树的右链，假设我们要插入的节点为 \(u\)，找到右链上最后一个权值小于等于它的节点令为 \(fa\)，且令其在树上的原右儿子为 \(v\)，接下来连边：

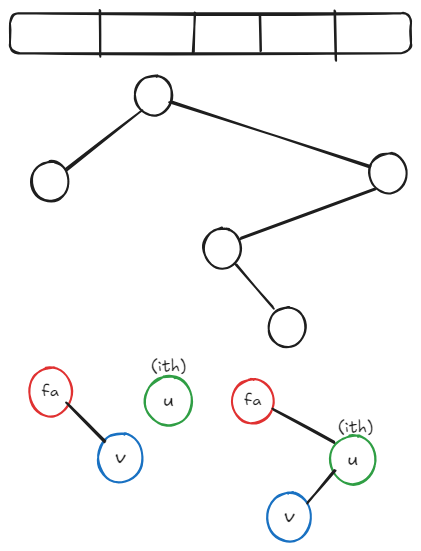
Image

观察到，每次操作后树都满足二叉搜索树与小根堆的性质。

好了！那么连边就完成了。完成若干次这样的连边，即可线性地建一颗完整的笛卡尔树。这样做的缺点是比较容易被卡，当权值为单调不降序列，该树可能退化成一条链。

代码贴贴

（舍弃简洁性换可读性zz）

点击查看代码 
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e7+5;
int n,p[N],ans1,ans2;
int rt;
struct Node{
	int ls,rs,fa;
	int val;
}tre[N];
int stk[N],tp;
void ins(int u,int va){
	while(tp&&tre[stk[tp]].val>va)tp--;//手写单调栈
	if(!tp){
		tre[rt].fa=u;//没有比u小的节点 
		tre[u].ls=rt;//令u为根节点且左儿子为原根节点
		//符合编号二叉搜索树性质 
		rt=u;
	}
	else {
		int fa=stk[tp],v=tre[fa].rs;
		tre[v].fa=u;tre[u].ls=v;//v->u
		tre[fa].rs=u;tre[u].fa=fa;//u->fa
	}
	tre[u].val=va;
	stk[++tp]=u;
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>p[i];
		ins(i,p[i]);
	}
	for(int i=1;i<=n;i++){
		ans1^=i*(tre[i].ls+1);
		ans2^=i*(tre[i].rs+1);
	}
	cout<<ans1<<' '<<ans2;
	return 0;
}

例题

SP3734 PERIODNI - Periodni

根据题意，我们可以大致想到一个树上 DP 的思路（\(f[u][k]\) 在节点 \(u\)，子树内共放 \(k\) 个数）。每次划分矩形，假设当前节点所代表的矩形长为 \(a\) 宽为 \(b\)，如果是叶子节点（边界条件）有：

\[\begin{aligned} f[u][k]=C_a^k C_b^kA_k^k \end{aligned} \]

img

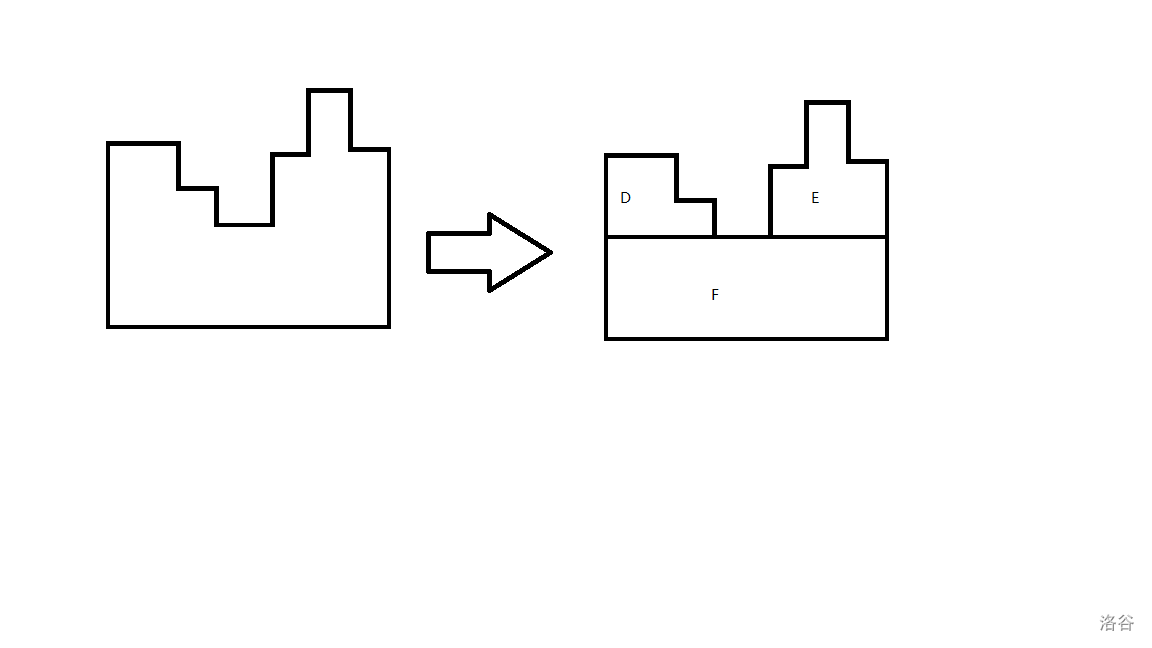
（From SP3734，侵删）

转移来说，不难推出：

\[\begin{aligned} f[u][k]=\sum_{i=0}^k\sum_{j=0}^{k-i}f[ls][i]\times f[rs][j]\times C_{a-i-j}^{k-i-j} C_b^{k-i-j}A_{k-i-j}^{k-i-j} \end{aligned} \]

这个式子是 \(O(nk^3)\) 的，考虑优化，这是一个类似加法卷积的形式，观察到有大量重复的 \(i,j\) 在不同的 \(k\) 中被使用，预处理出下式即可：

\[\begin{aligned} g[u][p]&=\sum_{i+j=p}f[ls][i]\times f[rs][j]\\ f[u][k]&=\sum_{p=0}^k g[u][p]\times C_{a-p}^{k-p} C_b^{k-p}A_{k-p}^{k-i-j} \end{aligned} \]

点击查看代码 
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=500+5,MOD=1e9+7,INF=1e12,M=1e6;
int n,k,ans1,ans2;
int rt;
struct Node{
	int ls,rs,fa;
	int val;
}tre[N];
int stk[N],tp;
void ins(int x,int va){
	while(tp&&tre[stk[tp]].val>va)tp--;
	if(!tp){
		if(rt)tre[rt].fa=x;
		tre[x].ls=rt;
		rt=x;
	}
	else {
		int u=stk[tp],rsu=tre[u].rs;
		tre[rsu].fa=x;tre[x].ls=rsu;
		tre[u].rs=x;tre[x].fa=u;
	}
	tre[x].val=va;
	stk[++tp]=x;
}
int p[N],dp[N][N],jc[M+5],mn[N],mx[N];
int ny[M+5];
void init(){
	jc[0]=1;ny[0]=ny[1]=1;
	for(int i=2;i<=M;i++)ny[i]=(MOD-MOD/i)*ny[MOD%i]%MOD;
	for(int i=2;i<=M;i++)ny[i]=ny[i-1]*ny[i]%MOD;
	for(int i=1;i<=M;i++)jc[i]=jc[i-1]*i%MOD;
}
int inv(int x){
	return ny[x];
}
int C(int m,int n){
	if(n>m||n<0)return 0;
	if(n==m||n==0)return 1;
	return jc[m]*inv(n)%MOD*inv(m-n)%MOD;
}
int cho(int row,int col,int v){
	return C(row,v)*C(col,v)%MOD*jc[v]%MOD;
}
int plu(int x,int y){
	return (x%MOD+y%MOD+MOD)%MOD;
}
int sz(int u){
	return mx[u]-mn[u]+1;
}
int g[N];
void dfs(int u,int mns){
	if(!u)return ;
	dp[u][0]=1;
	int ls=tre[u].ls,rs=tre[u].rs,uh=p[u]-mns;
	if(!ls&&!rs){
		for(int i=1;i<=k;i++)dp[u][i]=cho(sz(u),uh,i);
		return ;
	}
	if(!ls||!rs){
		int v;
		if(!ls)v=rs;
		else v=ls;
		dfs(v,p[u]);
		g[0]=1;
		for(int i=1;i<=k;i++)g[i]=0;
		for(int i=1;i<=k;i++)
			g[i]=plu(g[i],dp[v][i]%MOD);
		dp[u][0]=1;
		for(int i=1;i<=k;i++)
			for(int j=0;j<=i;j++)
				dp[u][i]=plu(dp[u][i],g[j]*cho(sz(u)-j,uh,i-j)%MOD);
		return ;
	}
	dfs(ls,p[u]);
	dfs(rs,p[u]);
	g[0]=1;
	for(int i=1;i<=k;i++)g[i]=0;
	for(int i=1;i<=k;i++)
		for(int j=0;j<=i;j++)
			g[i]=plu(g[i],dp[ls][j]*dp[rs][i-j]%MOD);
	dp[u][0]=1;
	for(int i=1;i<=k;i++)
		for(int j=0;j<=i;j++)
			dp[u][i]=plu(dp[u][i],g[j]*cho(sz(u)-j,uh,i-j)%MOD);
}
void rdfs(int x){
	if(!x)return ;
	mn[x]=mx[x]=x;
	rdfs(tre[x].ls);
	rdfs(tre[x].rs);
	if(tre[x].ls){
		mn[x]=min(mn[x],mn[tre[x].ls]);
		mx[x]=max(mx[x],mx[tre[x].ls]);
	}
	if(tre[x].rs){
		mn[x]=min(mn[x],mn[tre[x].rs]);
		mx[x]=max(mx[x],mx[tre[x].rs]);
	}
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	cin>>n>>k;init();dp[0][0]=1;
	for(int i=1;i<=n;i++){
		cin>>p[i];
		ins(i,p[i]);
	}
	rdfs(rt);
	dfs(rt,0);
	cout<<dp[rt][k];
	return 0;
}

P1377 [TJOI2011] 树的序

观察题目，给的键值其实就相当于 \(key\)，把输入顺序作为优先级 \(pri\) 按照 \(key\) 升序排序后建出笛卡尔树，然后输出先序遍历即可。

点击查看代码 
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
int n,ans1,ans2;
int rt;
struct Node{
	int ls,rs,fa;
	int val;
}tre[N];
int stk[N],tp;
void ins(int x,int va){
	while(tp&&tre[stk[tp]].val>va)tp--;
	if(!tp){
		if(rt)tre[rt].fa=x;
		tre[x].ls=rt;
		rt=x;
	}
	else {
		int u=stk[tp],rsu=tre[u].rs;
		tre[rsu].fa=x;tre[x].ls=rsu;
		tre[u].rs=x;tre[x].fa=u;
	}
	tre[x].val=va;
	stk[++tp]=x;
}
void dfs(int x){
	if(!x)return ;
	cout<<x<<' ';
	if(tre[x].ls<tre[x].rs){
		dfs(tre[x].ls);
		dfs(tre[x].rs);
	}
	else {
		dfs(tre[x].rs);
		dfs(tre[x].ls);
	}
}
int p[N];
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++){
		int id;cin>>id;
		p[id]=i;
	}
	for(int i=1;i<=n;i++){
		ins(i,p[i]);
	}
	dfs(rt);
	return 0;
}

P4755 Beautiful Pair

利用经典性质，每次左右子树中的节点匹配（左右子树都可以包含根节点），我们需要保证建出的树不是太劣，然后在上面类似于分治地处理，其实想到可以每次在左右子树中选一个 \(siz\) 较小的，然后数据结构维护另一个子树的信息（下标为 \(a_i\)，值为 \(cnt\)），计入答案即可。可以保证这样的时间在 \(O(n\log n)\) 内（参考树上启发式合并），加上数据结构可以做到 \(O(n\log^2 n)\)。

点击查看代码 
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=4e6+5;
int n,p[N];
int rt;
struct Tre{
	int tt[N];
	int lowbit(int x){return x&-x;}
	void ins(int p,int x){for(int i=p;i<=n;i+=lowbit(i))tt[i]+=x;}
	int que(int p){int rs=0;for(int i=p;i;i-=lowbit(i)){rs+=tt[i];}return rs;}
}T;
struct Node{
	int ls,rs,fa;
	int val;
}tre[N];
int cnt;
struct Q{
	int r,lim,id,opt;
}qs[N],dt[N];
int stk[N],tp;
void ins(int x,int va){
	while(tp&&tre[stk[tp]].val<va)tp--;
	int u,rsu;
	if(!tp)u=0,rsu=rt;
	else u=stk[tp],rsu=tre[u].rs;
	tre[rsu].fa=x;tre[u].rs=x;
	tre[x].fa=u;tre[x].ls=rsu;
	tre[x].val=va;
	if(!tp)rt=x;
	stk[++tp]=x;
}
int ans;
void dfs(int u,int l,int r){
	if(!u)return ;
	int lsiz=u-l,rsiz=r-u;
	int ls=tre[u].ls,rs=tre[u].rs;
	dfs(ls,l,u-1);dfs(rs,u+1,r);
	if(lsiz<=rsiz)
		for(int i=l;i<=u;i++){
			qs[++cnt]=(Q){u-1,p[u]/p[i],1,-1};
			qs[++cnt]=(Q){r,p[u]/p[i],1,1};
		}
			
	else 
		for(int i=u;i<=r;i++){
			qs[++cnt]=(Q){l-1,p[u]/p[i],1,-1};
			qs[++cnt]=(Q){u,p[u]/p[i],1,1};
		}
}
bool cmp(Q x,Q y){
	if(x.lim==y.lim)return x.id<y.id;
	return x.lim<y.lim;
}
void cdq(int l,int r){
	if(l>=r)return ;
	int mid=(l+r)>>1;
	cdq(l,mid);cdq(mid+1,r);
	int nl=l,cpt=0,cgt=l;
	for(int nr=mid+1;nr<=r;nr++){
		while(nl<=mid&&qs[nl].r<=qs[nr].r){
			if(!qs[nl].id)cpt++;
			dt[cgt++]=qs[nl++];
		}
		ans+=qs[nr].opt*cpt;
		dt[cgt++]=qs[nr];
	}
	while(nl<=mid)dt[cgt++]=qs[nl++];
	for(int i=l;i<=r;i++)qs[i]=dt[i];
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>p[i];
		ins(i,p[i]);
	}
	dfs(rt,1,n);
	for(int i=1;i<=n;i++){
		qs[++cnt]=(Q){i,p[i],0,0};
	}
	sort(qs+1,qs+1+cnt,cmp);
	cdq(1,cnt);
	cout<<ans;
	return 0;
}

[NFLSOJ]我们

Problem：给定一个长度为 \(n\) 的序列 \({a_n}\)，求有多少对 \([l,r]\) 满足：

\[(a_l\cup a_{l+1}\cup\dotsc\cup a_r)\oplus (a_l\cap a_{l+1}\cap\dotsc\cap a_r)\geq \max(a_l,a_{l+1},\dotsc,a_r) \]

（多测，\(\sum n\le 10^6\)）

观察到一个核心性质，一个区间向外扩展，它的贡献 \(W=(a_l\cup a_{l+1}\cup\dotsc\cup a_r)\oplus (a_l\cap a_{l+1}\cap\dotsc\cap a_r)\) 单调不减。利用这个性质，我们先对序列建出大根堆笛卡尔树，然后在笛卡尔树上选取 \(u\) 的左右子树中较小的一个进行暴力枚举（作为左端点或右端点），其对应的区间可以二分出来。根据启发式合并这样做总共是 \(O(n\log^2 n)\) 的，卡卡能过。

点击查看代码 
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=1e6+5;
int n,rt;
LL a[N];
int stk[N],tp;
struct Node{
	int lc,rc,fa;
	LL val;
}t[N];
inline void clr(int x){t[x].lc=t[x].rc=t[x].fa=0;t[x].val=0;}
void insert(int x){
	while(tp&&t[stk[tp]].val<t[x].val)tp--;
	if(!tp){
		t[rt].fa=x;
		t[x].lc=rt;
		rt=x;
	}
	else {
		int u=stk[tp],rc=t[u].rc;
		t[rc].fa=x;t[x].lc=rc;
		t[u].rc=x;t[x].fa=u;
	}
	stk[++tp]=x;
}
int L[N],R[N],lg2[N];
LL lor[N][21],land[N][21];
LL qor(int l,int r){
	int siz=lg2[r-l+1];
	return lor[l][siz]|lor[r-(1<<siz)+1][siz];
}
LL qand(int l,int r){
	int siz=lg2[r-l+1];
	return land[l][siz]&land[r-(1<<siz)+1][siz];
}
LL ans;
void dfs(int u){
	L[u]=u,R[u]=u;
	if(t[u].lc)dfs(t[u].lc),L[u]=min(L[u],L[t[u].lc]);
	if(t[u].rc)dfs(t[u].rc),R[u]=max(R[u],R[t[u].rc]);
	if(u-L[u]+1<=R[u]-u+1){
		for(int i=L[u];i<=u;i++){
			int l=u,r=R[u],res=R[u]+1;
			while(l<=r){
				int mid=(l+r)>>1;
				if((qor(i,mid)^qand(i,mid))>=t[u].val)res=mid,r=mid-1;
				else l=mid+1;
			}
			ans+=R[u]-res+1;
		}
	}
	else {
		for(int i=u;i<=R[u];i++){
			int l=L[u],r=u,res=L[u]-1;
			while(l<=r){
				int mid=(l+r)>>1;
				if((qor(mid,i)^qand(mid,i))>=t[u].val)res=mid,l=mid+1;
				else r=mid-1;
			}
			ans+=res-L[u]+1;
		}
	}
}
int main(){
	//freopen("us.in","r",stdin);
	//freopen("us.out","w",stdout);
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	int T;cin>>T;
	lg2[1]=0;t[0].val=(1ll<<61);
	for(int i=2;i<=N-5;i++)lg2[i]=lg2[i>>1]+1;
	while(T--){
		cin>>n;rt=0;ans=0;tp=0;
		for(int i=1;i<=n;i++)
			cin>>a[i],clr(i),
			t[i].val=a[i],insert(i),
			lor[i][0]=land[i][0]=a[i];
		for(int j=1;(1<<j)<=n;j++)
			for(int i=1;i+(1<<j)-1<=n;i++){
				lor[i][j]=lor[i][j-1]|lor[i+(1<<(j-1))][j-1],
				land[i][j]=land[i][j-1]&land[i+(1<<(j-1))][j-1];
			}
		dfs(rt);
		cout<<ans<<'\n';
	}
	return 0;
}
posted @ 2025-04-24 14:53  TBSF_0207  阅读(25)  评论(0)    收藏  举报