(笔记)网络流 费用流 二分图匹配 霍尔定理 图论建模
声明:本博客并不保证严谨全面,只是笔者的个人笔记,如有错误欢迎指出,也同时欢迎补充缺漏内容。
网络流最大初步
定义
什么是最大流
类比一个供水问题,有 \(s\) 作为自来水公司,\(t\) 作为供水地点,\(s\) 与 \(t\) 通过若干条有向边连接,每条边有一个固定容量 \(w\),单位时间内流经的水量不能超过容量,求单位时间内能从 \(s\) 汇入 \(t\) 的最大水量。
由题面不难得知,一条路径上的最大流速,取决于这条路的“瓶颈”,即容量最小的边。
一些定义:
源点:题目中的 \(s\)
汇点:题目中的 \(t\)
最大流求解性质:
流量守恒:从源点 \(s\) 流到汇点 \(t\) 的了,流量相等,对于中转点,流入与流出相等。
反对称性:从 \(u\) 到 \(v\) 的流量记作 \(w_{u,v}\),则从 \(v\) 到 \(u\) 的流量 \(w_{v,u}=-w_{u,v}\)
容量限制:每条边的实际流速不得大于容量。
FF、EK、Dinic算法
这里不进行过于详细的介绍,更多信息请见command_block大佬的blog
核心思想
首先 Brute-Force 思想容易想到从 \(s\) 流到 \(t\) 需要进行搜索,将搜索到的 \(s\) 到 \(t\) 的路径上最小容量记下,将路径上边权(容量)都减去此值,然后反复迭代直到没有路径可选。
这样显然是错误的,考虑到搜索时不一定每次都正好选到正确的那条边,而且前一次搜索可能会影响后一次。
- 残留网络,注意到每次搜索路径时需消除对下一次搜索的影响,所以需要在原有路径上建一条反向路径,这就相当于给程序一个反悔的机会(所以最大流思想和反悔贪心类似,因为这类贪心是最大流算法的基础)。
下图有助于理解残留网络的原理:
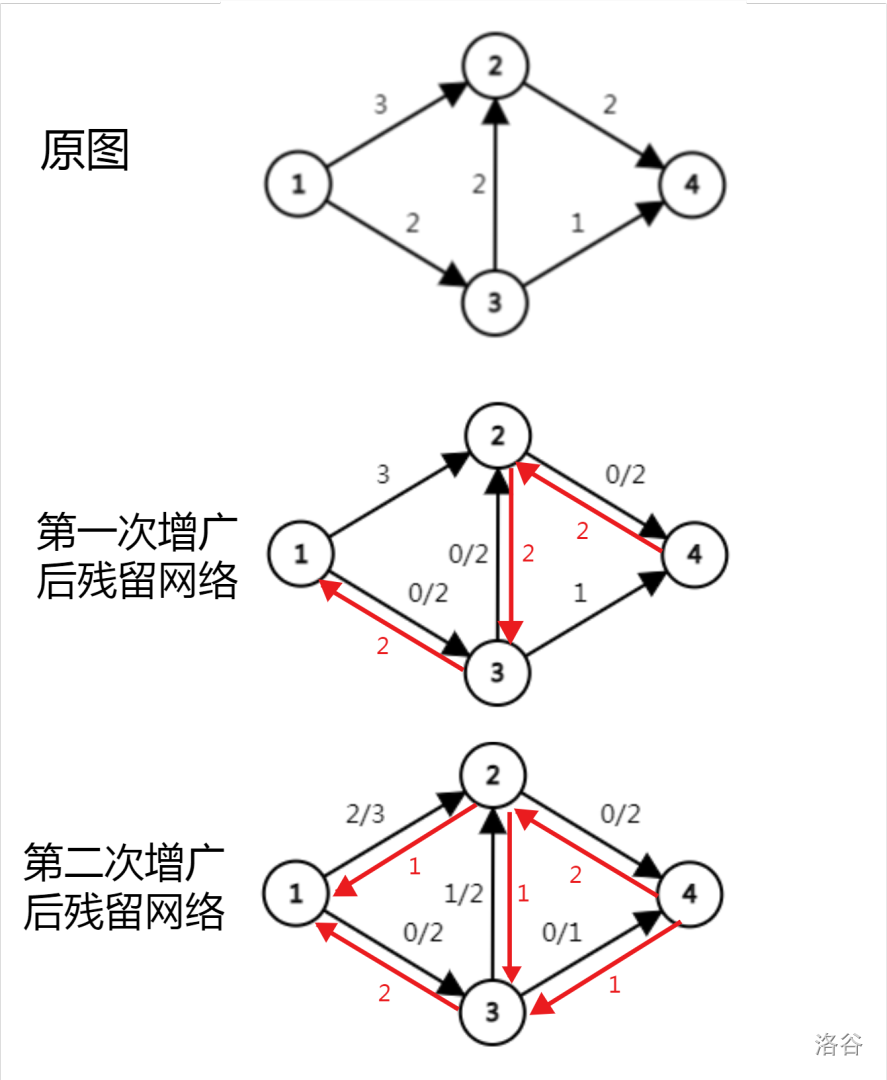
(图中第一次搜索路径为 \(1\) -> \(3\) -> \(2\) -> \(4\))
以第一次增广后残留网络分析,得到一条 \(1\) -> \(2\) -> \(3\) -> \(4\) 的增广路径,路径上最小容量为 \(1\)。
第二次增广利用了反向边 \(2\) -> \(3\),相当于让第一次路径的一部分流量返回节点\(3\)然后通过 \(3\) -> \(4\) 到达最终节点。
为什么这样是对的?
对于边 \(1\) -> \(2\),程序将它的流量连接至 \(2\) -> \(3\) -> \(4\) 上,但实际上它的流量贡献给了 \(2\) -> \(4\)。
对于边 \(3\) -> \(2\),它返回了 \(1\) 的流量,而贡献了\(1\)的流量到 \(2\) -> \(4\)。
对于边 \(2\) -> \(4\)共获得来自 \(1\) -> \(2\) 和 \(3\) -> \(2\) 的 \(2\) 点流量,所以网络仍然是正确的。
对于边 \(3\) -> \(4\),它获得了来自 \(3\) -> \(2\) 返回的 \(1\) 点流量,然后通过 \(3\) -> \(4\) 流向终点 \(4\)。
通过以上过程,可以感性理解残留网络增广原理,以及为什么 每次累加增广路径上的最小容量。
初学时对工作原理十分疑惑,因为看上去第二次增广后是把自己的流量贡献到 \(2\) -> \(3\) -> \(4\) 上了。其实第二次增广路径可以分成两部分,\(2\) -> \(3\) -> \(4\) 部分是帮助原有流量返回,不损失流量。而实际上,\(1\) -> \(2\) 将自己的流量贡献给了 \(2\) -> \(4\),和之前未返回的流一起通过 \(2\) -> \(4\) 流向终点。
(此说明并不严谨,希望能帮助你理解工作原理)
注意原边同其反向边权值和恒为原边容量。
-
增广路径,即残留网络上 \(s\) 到 \(t\) 的一条路径
-
割,指在原图中移除部分边,使 \(s\) 无法流到 \(t\)
Ford-Fulkerson算法:不断暴力迭代,可能陷入长时间不必要的迭代,时间取决于增广路径搜索次数。
Edmonds-Karp算法:在前者基础上,每次用 BFS 计算一条最短的增广路径,时间复杂度为 \(O(nm^2)\)。
Dinic算法:惯用算法,泛用性最强,每次用 BFS 构造分层图,限制 DFS 搜索范围,分层图中任意路径都是边数最少的路径。DFS 寻找增广路,受限制只能沿 BFS 规定层数往下找,不会绕路,理论时间复杂度为 \(O(n^2m)\)。
-
当前弧优化
记录当前有哪些流不出流量的边,下次来就不试了,这样不会重复遍历同一边,时间严格在 \(O(nm)\) 内。
-
点优化
把当前弧优化的边换成了点,如果一个点不再流出流量,那么直接把 \(dep\leftarrow +\infty\),多数时候只能优化常数。
-
不完全 BFS 优化
在 BFS 到 \(T\) 的时候就停止,因为后面路径一定更长,随机数据下表现优良。
下面是模板的Dinic算法代码:(附当前弧优化)
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=205,M=5005,INF=3e9;
int n,m,s,t;
int head[N],idx=1;
struct Edge{
int v,next,w;
}adj[M<<1];
void ins(int x,int y,int z){
adj[++idx].v=y;
adj[idx].next=head[x];
adj[idx].w=z;
head[x]=idx;
}
int now[N],dep[N];
bool bfs(){
for(int i=1;i<=n;i++)dep[i]=INF;
dep[s]=0;
now[s]=head[s];
queue<int>Q;Q.push(s);
while(!Q.empty()){
int u=Q.front();Q.pop();
for(int i=head[u];i;i=adj[i].next){
int v=adj[i].v,w=adj[i].w;
if(w>0&&dep[v]==INF){
Q.push(v);
now[v]=head[v];
dep[v]=dep[u]+1;
if(v==t)return 1;//不完全 BFS 优化
}
}
}
return 0;
}
int dfs(int u,int sum){
if(u==t)return sum;
int k,flow=0;
for(int i=now[u];i&&sum>0;i=adj[i].next){
now[u]=i;//当前弧优化
int v=adj[i].v,w=adj[i].w;
if(w>0&&dep[v]==dep[u]+1){
k=dfs(v,min(sum,w));
if(k==0)dep[v]=INF;//点优化
adj[i].w-=k;
adj[i^1].w+=k;
flow+=k;sum-=k;
}
}
return flow;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n>>m>>s>>t;
for(int i=1;i<=m;i++){
int u,v,w;
cin>>u>>v>>w;
ins(u,v,w);
ins(v,u,0);
}
int ans=0;
while(bfs())ans+=dfs(s,INF);
cout<<ans;
return 0;
}
网络最大流惯用策略
理论知识
请前往(笔记)二分图最大匹配这里有相关介绍。
补充一个最小割定理。
有源汇割:一个边集,删去之后使得源汇不连通,而且其中任意一条边不割,则造成源汇连通(割是紧的)。
有源汇最小割:一个有向图,边有边权(一般为正,这里的边权就是容量),要求割去权值和最小的边集使得源汇不连通。
定理:
\(\text{最小割}=\text{最大流}\)
证明:
\(\text{①最大流}\le\text{最小割}\)
首先根据割的定义,所有的流都必然经过割边集中的某一条边,那么流量总和最大就是割边集总和。
\(\text{②最大流}\geq\text{最小割}\)
考虑我们求出了一个最大流,那么某些边会成为瓶颈,即残量网络上为 \(0\)。
这些边一定分布成为一个割,否则仍然会有增广路。
——网络流/二分图相关笔记(干货篇)-command_block
注意在②中,如果一个流上存在多个瓶颈,取任意一个构造,不会对最终结果造成影响。考虑如果多个流共享一个瓶颈,那么这个瓶颈可以被拆成多个部分,每个部分分别对应每个流的流量,所以随便选都可以构造出一个割。
自主建模
1. 枚举时间类
如题,每个太空飞船可能错开流动,枚举时间的话只需要每个时间点加相应边,以时间点和站点信息独立为一个点,然后跑最大流,每次累加直到满足条件,同时判断连通性即可。
2. 二分图最大匹配
这是一类比较经典的应用,在二分图中加入超级汇点和超级源点,左侧所有点连接超级源点,右侧所有点连接超级汇点。
一般时权值为1(即经典最大匹配问题),必要时加入权值,即相当于加入了多个点,然后跑最大流。
3. 二分图匹配变式
(1)同时存在问题(限制类、独立集问题)
此类问题关键限制一般是“不能同时选什么”。
这类问题关键在于将格子分为互相区分的两类,并且不能同时存在的相互连边(二分图异集),然后跑最大匹配。
注意到两类必须要能相互转化,需要找到一个性质,使不能同时存在条件转化时,这个性质也不断反转,使得同个集的点性质一样,不同集性质不同。
接下来只需要运用二分图独立集定理=总节点数-最小覆盖=总节点数-最大匹配即可。
在上题中,此性质为格子的奇偶性,即\((x+y)\)的奇偶性,相当于将格子相邻都染成不同的颜色。
注意P5030 长脖子鹿放置这类较为特殊的类型需要寻找性质,如上题性质就不是格子奇偶性,而是行或列奇偶性。
(2)流动问题
这类问题利用了二分图的性质,同样是加入超级源点与汇点,然后改变连接时的权值为人数,方案通过反向边判断。
(3)二分图性质定理
此类题目灵活运用(笔记)二分图最大匹配中提到的定理,通过数字关系求出答案,具体情况具体分析。
最小费用最大流
费用流初步
关于如何求最小费用最大流:
只需要将求最大流算法中的BFS部分改为不是判断分层图,而是跑一遍最短路算法即可。考虑到负边权和负环一般不可避免(反向边需要负权,以保证回流时费用减少),使用Bellman-Ford算法(SPFA算法) 寻找增广路,保证费用最小的前提下在增广路上进行原算法操作即可。
详细证明不在此展开,因为这不是这篇博客的重点。
注意跑 SPFA 区别于普通最短路特点是相当于只找正容量边(增广路),且允许一个点多次入队,但不能使一个节点多次出现在队列中。在没有堆优化的前提下,可以找到一条从源点到汇点的增广路,使得其费用最小化。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e3+5,M=5e4+5,LEN=1e6+5,INF=3e9;
int n,m,s,t;
int head[N],idx=1;
struct Edge{
int v,next,w,c;
}adj[M<<1];
int ans,pay,pre[N],dis[N],preve[N];
void ins(int x,int y,int z,int c){
adj[++idx].v=y;adj[idx].next=head[x];//每次正反建边
head[x]=idx;adj[idx].w=z;adj[idx].c=c;
adj[++idx].v=x;adj[idx].next=head[y];
head[y]=idx;adj[idx].w=0;adj[idx].c=-c;//回流需要同时返回原来费用
}
int Q[LEN],hd,tl;
bool spfa(){
bool vis[N];
for(int i=1;i<=n;i++){pre[i]=-1;dis[i]=INF;vis[i]=0;}
dis[s]=0;
hd=1;tl=0;Q[++tl]=s;//手写队列
vis[s]=1;
while(hd<=tl){
int u=Q[hd++];
vis[u]=0;
for(int i=head[u];i;i=adj[i].next){
int v=adj[i].v,w=adj[i].w,c=adj[i].c;
if(w>0&&dis[u]+c<dis[v]){
dis[v]=dis[u]+c;
pre[v]=u;//记录每个节点前驱,方便寻找增广路
preve[v]=i;
if(!vis[v]){
vis[v]=1;
Q[++tl]=v;
}
}
}
}
return dis[t]!=INF;
}//spfa寻找增广路过程
int flow;
void sr(int u){
if(pre[u]!=-1){
flow=min(flow,adj[preve[u]].w);
sr(pre[u]);
adj[preve[u]].w-=flow;
adj[preve[u]^1].w+=flow;
pay+=flow*adj[preve[u]].c;
}//沿着增广路对容量进行修改,并沿途增加费用
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n>>m>>s>>t;
for(int i=1;i<=m;i++){
int u,v,w,c;
cin>>u>>v>>w>>c;
ins(u,v,w,c);
}
while(spfa())flow=INF,sr(t),ans+=flow;
cout<<ans<<' '<<pay;
return 0;
}
费用流建模基本类型
1. 拆点
很多费用流题目都利用了此技巧,即将定好的点拆成两个或多个部分,分别加入费用流运行。
这三题都是拆点技巧的典型运用,事实上,很大一部分费用流题目都运用了此技巧。如果细化,大概有这两个类型:
-
拆两点,一般用于一个点只能经过一次的图问题,或用于解决特殊的贪心问题,拆点后两点用流量为\(1\),费用为\(0\)的边相连后即可解决。
-
拆多点,一般是等待时间类问题,得到方程后通过对单一点的分析,将一对多转为一对一的单匹配。
2. 负容量问题
内容有待补充
3. 遗传类问题
此类问题类似于仓库存储,关键在于随时间流逝可以遗传货物至下一时间段。那么以时间段为点建模,连续时间顺次相连,每个点都与超级源点与超级汇点都连边即可。
上下界网络流
待补充
总结
最后,网络流类问题代码实现难度一般不大,关键在于建模。建模需要结合套路与充分发挥发散性思维,也是考验竞赛者基本功的重要题型。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号