题解:P4115 Qtree4
全局平衡二叉树
本文可能较长,但请相信仅仅是因为较详细的缘故,而不是有多复杂。
这是一种(较)纯正的全局平衡二叉树解法。
刚学这个东西,这里主要借鉴了hehezhou大佬的题解。该题解末尾提到,作者的全局平衡二叉树融入了宗法树的特征,即数字都存储在叶子结点里的一种类线段树(Leafy Tree)。那么本篇题解将有所不同,提供一个较为普适的全局平衡二叉树写法(Nodely Tree),顺便详细展开一些自己关于该结构适用性与这题细节的一些想法(顺便修一下之前题解可能出现的一些笔误)。如有差错,敬请指出。
朴素解法
我们都知道(?)存在这么一种解法,对原树进行重链剖分,然后对每条重链维护一个线段树,每个点维护一个堆。线段树内由于是链状结构,可以直接对信息进行合并。堆维护的是每个节点到自己轻子树内所有节点的所有距离。这样每次修改需要向上跳 \(O(\log n)\) 条链,线段树修改每次为 \(O(\log n)\),每次对堆内(仅需修改每条链链顶的父亲)信息的修改为 \(O(\log n)\),总共就是 \(O(n\log^2 n)\) 的。
这里我们可以展开讲一下线段树的维护(可删堆就不讲了)。对于一个线段树上节点 \(u\) 及其代表的区间 \([u_l,u_r]\),它的左儿子 \(ls\),右儿子 \(rs\),分别维护三个信息。
- \(u_{lmax}\) 表示 \([u_l,u_r]\) 内白点到 \(u_l\) 的最大距离。
- \(u_{rmax}\) 表示 \([u_l,u_r]\) 内白点到 \(u_r\) 的最大距离。
- \(u_{ans}\) 表示 \([u_l,u_r]\) 内白点两两最大距离。
那么就有合并:
显然对于一条链上的维护是容易的。
全局平衡二叉树的应用
这里我们降复杂度主要有几个阻碍。
- 一个节点可能有多个轻儿子,导致需要开一个堆来维护,这让我们非常不悦。
- 我们在树剖的时候居然要跳 \(O(\log n)\) 次并且每次进行 \(O(\log n)\) 的操作,这让我们非常不悦。
第一个的解决方法就是@hehezhou 大佬提到的一般树二叉化。
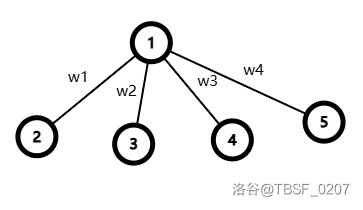
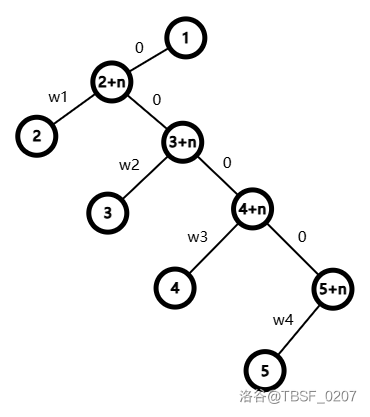
具体地,对于每个节点 \(u\),我们将它的每个儿子 \(v\) 都复制一个节点 \(rep(v)\),然后分类讨论,用 \(dep\) 记录距离。如果 \(v\) 是第一个儿子,连接 \(u\rightarrow rep(v)\) 和 \(rep(v)\rightarrow v\)。否则,令上一个儿子为 \(pre\),连接 \(rep(v)\rightarrow rep(pre),v\rightarrow rep(v)\)。
这样就完成了一般树向二叉树的转化。
第二个问题的解决方法就是全局平衡二叉树。这个东西实际上是一个静态的 LCT,要对一棵树进行重链剖分。对转化成的二叉树,先进行重链剖分。对于每条重链,每次 build 求它的加权重心(每个点的点权是轻儿子 \(siz+1\)),然后递归建树。
树高是 \(O(\log n)\) 的,这是全局平衡二叉树的复杂度保证。证明分类讨论即可,无论是跳重边还是跳轻边,子树大小至少都会翻倍。
我们建出了一颗全局平衡二叉树。由于第一个问题提供的解决方法,这棵树上的每一个节点至多有一个轻儿子,这是一个很好的性质。
下面就是和一般全局平衡二叉树和原有题解不同的地方。原有题解由于叶子节点没有儿子,可以直接把轻儿子接在二叉树的任意儿子上变成一个伪儿子,目的仅是便利访问和更新信息。但是我不想写宗法树!(这样我们就可以少开一半的节点)于是对每个节点额外开了一个 \(u_{vt}\),记录它的轻(虚)儿子所在二叉搜索树的根。
信息维护上,对于重边(实边)的上传,我们对二叉搜索树内的信息直接采用类线段树的做法合并。对于轻边(虚边)的上传,我们用一个微量的分类讨论解决,具体代码见下。
接下来的合并也有所不同。对于一个节点 \(u\),我们要先合并 \(ls,u\),再用合并过的 \(u\) 与 \(rs\) 合并,具体实现如下:
void merge(Node &ls,Node &rs,bool tf){//线段树的合并
Node u;
if(!tf)u=ls;
else u=rs;
u.lmax=max(ls.lmax,dep[rs.L]-dep[ls.L]+rs.lmax);
u.rmax=max(rs.rmax,dep[rs.R]-dep[ls.R]+ls.rmax);
u.ans=max(max(ls.ans,rs.ans),dep[rs.L]-dep[ls.R]+ls.rmax+rs.lmax);
if(!tf)u.R=rs.R,ls=u;
else u.L=ls.L,rs=u;
}
u.L=u.R=p;u.ans=u.lmax=u.rmax=(col[p]?0:-INF);
if(u.ch[0])merge(t[u.ch[0]],u,1);//先合并左儿子
if(u.ch[1])merge(u,t[u.ch[1]],0);//再合并右儿子
然后就是关于轻儿子的问题。这里我们要对线段树的信息定义做一些稍微的变形,\(u_{lmax}\) 表示 \(u_l\) 到当前所处集合中白点的距离最大值,\(u_{rmax},u_{ans}\) 同理。这样我们维护的就不再是一条链,但是由于每次合并都是在链首或者链尾进行的,所以只需要保证链首链尾信息的正确性,这个做法就是对的。
我们要怎么维护它们呢?令 \(lson_u\) 表示 \(u\) 的轻儿子。
实现如下:
if(u.vt){
int D=t[u.vt].lmax+dep[lson[p]]-dep[p];
u.ans=max(u.ans,t[u.vt].ans);
u.lmax=max(u.lmax,D+dep[p]-dep[u.L]);
u.rmax=max(u.rmax,D+dep[u.R]-dep[p]);
int D1=(t[u.ch[0]].rmax)+dep[p]-dep[t[u.ch[0]].R]+D,
D2=(t[u.ch[1]].lmax)+dep[t[u.ch[1]].L]-dep[p]+D;
u.ans=max(u.ans,max(D1,D2));
}
另外还要注意叶子节点的分讨,这里就不作详细展开了。
最后需要注意的是,本篇题解着重强调了 \(lson_u\) 和 \(u_{vt}\) 的区别,希望没有人像我一样混淆。
完整代码:
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5,INF=1e9;
int n,head[N],idx,lson[N],rson[N],dep[N];
int siz[N],lsiz[N],root;
struct Node{int ch[2],L,R,fa,lmax,rmax,ans,vt;}t[N];
struct Edge{int v,next,w;}e[N<<1];
void ins(int x,int y,int z){
e[++idx].v=y;
e[idx].next=head[x];
e[idx].w=z;
head[x]=idx;
}
void ins1(int x,int y){
if(!lson[y])lson[y]=x;
else rson[y]=x;
}
void dfs(int u,int fa){
int lst=0;
for(int i=head[u];i;i=e[i].next){
int v=e[i].v,w=e[i].w;
if(v==fa)continue;
dep[v]=dep[u]+w;
dep[v+n]=dep[u];
if(!lst){
ins1(v+n,u);
ins1(v,v+n);
}
else {
ins1(v+n,lst);
ins1(v,v+n);
}
dfs(v,u);
lst=v+n;
}
}
void dfs0(int u){
siz[u]=1;
if(lson[u])dfs0(lson[u]);
siz[u]+=siz[lson[u]];
if(rson[u])dfs0(rson[u]);
siz[u]+=siz[rson[u]];
if(siz[lson[u]]>siz[rson[u]])
swap(lson[u],rson[u]);
lsiz[u]=siz[lson[u]]+1;
}
int stk[N],tp,pre[N];
int ef(int l,int r,int &sum){
int res=r;
while(l<=r){
int mid=(l+r)>>1;
if(pre[mid]>=sum)res=mid,r=mid-1;
else l=mid+1;
}
return res;
}
int build(int l,int r){
if(l>r)return 0;
if(l==r)return t[stk[l]].L=t[stk[l]].R=stk[l];
int sum=((pre[r]-pre[l-1])>>1)+pre[l-1];
int i=ef(l,r,sum);
t[stk[i]].ch[0]=build(l,i-1);
t[stk[i]].ch[1]=build(i+1,r);
t[t[stk[i]].ch[0]].fa=t[t[stk[i]].ch[1]].fa=stk[i];
t[stk[i]].L=stk[l],t[stk[i]].R=stk[r];
return stk[i];
}
void dfs1(int u){
stk[++tp]=u;
if(rson[u])dfs1(rson[u]);
else {
for(int i=1;i<=tp;i++)pre[i]=pre[i-1]+lsiz[stk[i]];
int rt=build(1,tp);
if(!stk[0])root=rt;
else t[rt].fa=stk[0],t[stk[0]].vt=rt;
tp=0;
}
stk[0]=u;
if(lson[u])dfs1(lson[u]);
}
int cntw;
bool col[N];
void merge(Node &ls,Node &rs,bool tf){
Node u;
if(!tf)u=ls;
else u=rs;
u.lmax=max(ls.lmax,dep[rs.L]-dep[ls.L]+rs.lmax);
u.rmax=max(rs.rmax,dep[rs.R]-dep[ls.R]+ls.rmax);
u.ans=max(max(ls.ans,rs.ans),dep[rs.L]-dep[ls.R]+ls.rmax+rs.lmax);
if(!tf)u.R=rs.R,ls=u;
else u.L=ls.L,rs=u;
}
void pushup(int p){
Node &u=t[p];
if(u.L==u.R){
int D=t[u.vt].lmax+dep[lson[p]]-dep[p];
u.ans=t[u.vt].ans;
if(col[p])u.ans=max(u.ans,u.lmax=u.rmax=max(D,0));
else u.lmax=u.rmax=D;
return ;
}
u.L=u.R=p;u.ans=u.lmax=u.rmax=(col[p]?0:-INF);
if(u.ch[0])merge(t[u.ch[0]],u,1);
if(u.ch[1])merge(u,t[u.ch[1]],0);
if(u.vt){
int D=t[u.vt].lmax+dep[lson[p]]-dep[p];
u.ans=max(u.ans,t[u.vt].ans);
u.lmax=max(u.lmax,D+dep[p]-dep[u.L]);
u.rmax=max(u.rmax,D+dep[u.R]-dep[p]);
int D1=(t[u.ch[0]].rmax)+dep[p]-dep[t[u.ch[0]].R]+D,
D2=(t[u.ch[1]].lmax)+dep[t[u.ch[1]].L]-dep[p]+D;
u.ans=max(u.ans,max(D1,D2));
}
}
void init(int p){
if(!p)return ;
init(t[p].vt);
init(t[p].ch[0]),init(t[p].ch[1]);
pushup(p);
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n;cntw=n;
t[0].lmax=t[0].rmax=t[0].ans=-INF;
for(int i=1;i<n;i++){
int a,b,c;
cin>>a>>b>>c;
ins(a,b,c);
ins(b,a,c);
}
dfs(1,0);
dfs0(1);
dfs1(1);
for(int i=1;i<=n;i++)col[i]=1;
init(root);
int Q;cin>>Q;
while(Q--){
char c;cin>>c;
if(c=='C'){
int x;cin>>x;
col[x]^=1;
if(!col[x])cntw--;
else cntw++;
for(;x;x=t[x].fa)pushup(x);
}
else {
if(cntw)cout<<t[root].ans<<'\n';
else cout<<"They have disappeared.\n";
}
}
return 0;
}
经过实测,由于每个节点两次合并的常数原因,本做法虽然比原做法少开一半的节点,但在评测时间上并无优势甚至更劣,读者可自行选择。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号