第一章 统计学习及监督学习概论

1.1 统计学习

统计学习是概率论、统计学、信息论、计算理论、最优化理论及计算机科学等多个领域的交叉学科；它从数据出发，提取出数据的特征，抽象出数据的模型，发现数据中的知识，又回到对数据的分析与预测中去。

如果一个系统能够通过执行某个过程改进他的性能，这就是学习——Herbert A. Simon

1.2 统计学习的分类

1.2.1 基本分类

1. 监督学习

从标注数据中学习
监督学习的本质是学习输入到输出的映射的统计规律

1). 输入空间、特征空间和输出空间
2). 联合概率分布

监督学习假设输入与输出的随机变量\(X\)和\(Y\)遵循联合概率分布\(P(X,Y)\)。统计学习假设数据存在一定的统计规律，\(X\)和\(Y\)具有联合概率分布就是监督学习关于数据的基本假设。

3). 假设空间

模型属于优输入控件到输出空间的映射的集合，这个集合就是假设空间。

监督学习的模型可以是概率模型或非概率模型，由条件概率分布\(P(Y|X)\)或决策函数\(Y = f(X)\)表示。对具体的输入进行相应的输出预测是，写作\(P(y|x)\)或\(y = f(x)\)

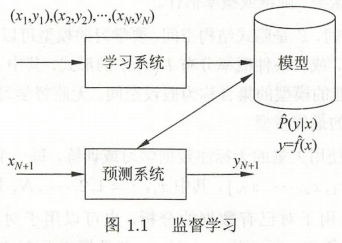
在预测过程中，预测系统对于给定的测试样本集中的输入\(x_{N+1}\)，由模型\(y_{N+1} = \arg\max\limits_{y}\hat{P}(y|x_{N+1})\)或\(y_{N+1} = \hat{f}(x_{N+1})\)给出相应的\(y_{N+1}\)
4). 问题的形式化
2. 无监督学习

从无标注数据中学习
本质是学习数据中的统计规律或潜在结构

3. 强化学习

强化学习是指智能系统在与环境的连续互动中学习最有行为策略的机器学习问题。
假设智能系统与环境的交互基于马尔可夫决策过程，智能系统能观测到的是与环境互动得到的数据序列。
强化学习的本质是学习最有的序贯决策。

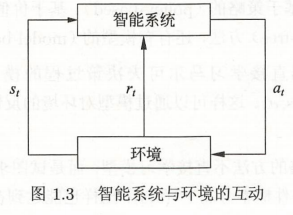
在每一步\(t\)，智能系统从环境中观测到一个状态\(s_t\)与一个奖励\(r_t\)，采取一个动作\(a_t\)。环境根据智能系统选择的动作，决定下一步\(t+1\)的状态\(s_{t+1}\)与奖励\(r_{t+1}\)。
要学习的策略表示为给定的状态下采取的动作。智能系统的目标不是短期奖励的最大化，而是长期积累奖励的最大化。
强化学习过程中，系统不断的试错，以达到学习最优策略的目的。

马尔可夫决策过程

• 马尔可夫性：下一个状态只依赖于前一个状态与动作
  价值函数定义为策略\(\pi\)从某一个状态\(s\)开始的长期累计奖励的数学期望：
  \(\tag{1.1}{v_{\pi}(s) = E_{\pi}[r_{t+1}+\gamma r_{t+2}+\gamma^2r_{t+3}+...|s_t = s,a_t = a]}\)
  动作价值函数定义为策略\(\pi\)的从某一个状态\(s\)和动作\(a\)开始的长期积累奖励的数学期望：
  \(\tag{1.2}{q_{\pi}(s,a) = E_{\pi}[r_{t+1}+\gamma r_{t+2}+\gamma^2r_{t+3}+...|s_t = s,a_t = a]}\)
  强化学习的目标就是在所有可能的策略中选出价值函数最大的策略\(\pi^*\)，而在实际学习中往往从具体的策略出发，不断优化已有策略。这里\(\gamma\)表示未来的奖励会有衰减。
• (半监督学习)

少量标注数据、大量未标注数据

• (主动学习)

机器不断主动给出实力让教师进行标注。监督学习可以看作是“被动学习”，主动学习的目标是找出对学习最有帮助的实例让教师标注，以较小的标注代价，达到较好的学习效果。

1.2.2 按模型分类

1. 概率模型与非概率模型

条件概率分布最大化后得到函数，函数归一化后得到条件概率分布。

2. 线性模型与非线性模型

3. 参数化模型与非参数化模型

参数化模型假设模型参数的维度固定，非参数化模型假设模型参数的维度不固定或者说无穷大。
参数化模型适合简单问题，现实问题使用非参数化模型更加有效。

1.2.3 按算法分类

在线学习与批量学习

• 在线学习——每次接受一个样本，进行预测，之后学习模型。

感知机是在线学习——每次接受一个输入\(x\)，用已有的模型计算损失函数loss func，更新模型，并不断重复。

• 批量学习一次接受所有数据，学习模型。之后进行预测。

1.2.4 按技巧分类

贝叶斯学习和核方法