拓扑排序笔记

原帖地址：https://blog.csdn.net/qq_35644234/article/details/60578189

1、拓扑排序的介绍

对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边(u,v)∈E(G)，则u在线性序列中出现在v之前。 
拓扑排序对应施工的流程图具有特别重要的作用，它可以决定哪些子工程必须要先执行，哪些子工程要在某些工程执行后才可以执行。为了形象地反映出整个工程中各个子工程(活动)之间的先后关系，可用一个有向图来表示，图中的顶点代表活动(子工程)，图中的有向边代表活动的先后关系，即有向边的起点的活动是终点活动的前序活动，只有当起点活动完成之后，其终点活动才能进行。通常，我们把这种顶点表示活动、边表示活动间先后关系的有向图称做顶点活动网(Activity On Vertex network)，简称AOV网。 
一个AOV网应该是一个有向无环图，即不应该带有回路，因为若带有回路，则回路上的所有活动都无法进行（对于数据流来说就是死循环）。在AOV网中，若不存在回路，则所有活动可排列成一个线性序列，使得每个活动的所有前驱活动都排在该活动的前面，我们把此序列叫做拓扑序列(Topological order)，由AOV网构造拓扑序列的过程叫做拓扑排序(Topological sort)。AOV网的拓扑序列不是唯一的，满足上述定义的任一线性序列都称作它的拓扑序列。

2、拓扑排序的实现步骤

1. 在有向图中选一个没有前驱的顶点并且输出
2. 从图中删除该顶点和所有以它为尾的弧（白话就是：删除所有和它有关的边）
3. 重复上述两步，直至所有顶点输出，或者当前图中不存在无前驱的顶点为止，后者代表我们的有向图是有环的，因此，也可以通过拓扑排序来判断一个图是否有环。

3、拓扑排序示例手动实现

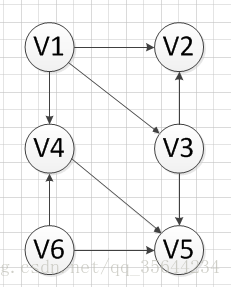
如果我们有如下的一个有向无环图，我们需要对这个图的顶点进行拓扑排序，过程如下： 

首先，我们发现V6和v1是没有前驱的，所以我们就随机选去一个输出，我们先输出V6，删除和V6有关的边，得到如下图结果： 

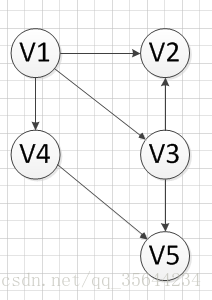
然后，我们继续寻找没有前驱的顶点，发现V1没有前驱，所以输出V1，删除和V1有关的边，得到下图的结果： 

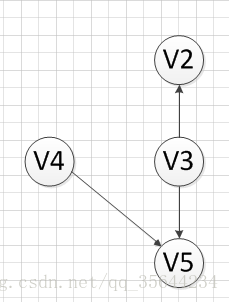
然后，我们又发现V4和V3都是没有前驱的，那么我们就随机选取一个顶点输出（具体看你实现的算法和图存储结构），我们输出V4，得到如下图结果： 

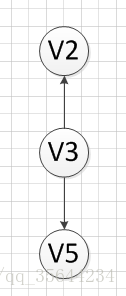
然后，我们输出没有前驱的顶点V3，得到如下结果： 

然后，我们分别输出V5和V2，最后全部顶点输出完成，该图的一个拓扑序列为：

v6–>v1—->v4—>v3—>v5—>v2

4、拓扑排序的代码实现

下面，我们将用两种方法来实现我么的拓扑排序：

1. Kahn算法
2. 基于DFS的拓扑排序算法

首先我们先介绍第一个算法的思路： 
Kahn的算法的思路其实就是我们之前那个手动展示的拓扑排序的实现，我们先使用一个栈保存入度为0 的顶点，然后输出栈顶元素并且将和栈顶元素有关的边删除，减少和栈顶元素有关的顶点的入度数量并且把入度减少到0的顶点也入栈。具体的代码如下：

#include<bits/stdc++.h>
using namespace std;

const int maxN=1000;
int N;

vector<int> G[maxN];
stack<int> s;
vector<int> topo;
int cnt[maxN];

void init(){
    memset(cnt,0,sizeof(cnt));
    while(!s.empty())s.pop();
    for(int i=1;i<=N;i++){
        for(int j=0;j<G[i].size();j++){
            cnt[G[i][j]]++;
        }
    }
}

bool toposort(){
    init();
    for(int i=1;i<=N;i++)if(cnt[i]==0){
        s.push(i);
        topo.push_back(i);
    }
    while(!s.empty()){
        int u=s.top();
        s.pop();
        for(int i=0;i<G[u].size();i++){
            cnt[G[u][i]]--;
            if(cnt[G[u][i]]==0){
                s.push(G[u][i]);
                topo.push_back(G[u][i]);
            }
        }
    }
    if(topo.size()==N)return true;
    else return false;
}

int main(){
    G[1].push_back(2);
    G[2].push_back(3);
    G[4].push_back(3);
    N=4;
    if(toposort())for(int i=0;i<topo.size();i++)cout<<topo[i]<<' ';
}

现在，我们来介绍第二个算法的思路： 
其实DFS就是深度优先搜索，它每次都沿着一条路径一直往下搜索，知道某个顶点没有了出度时，就停止递归，往回走，所以我们就用DFS的这个思路，我们可以得到一个有向无环图的拓扑序列，其实DFS很像Kahn算法的逆过程。具体的代码实现如下：

#include<bits/stdc++.h>
using namespace std;

const int maxN=1000;
int N;

vector<int> G[maxN];
int topo[maxN];
int vis[maxN];
int cnt;

bool dfs(int x){
    vis[x]=-1;    //标志正在访问中
    for(int i=0;i<G[x].size();i++){
        if(vis[G[x][i]]<0)return false;
        else if(vis[G[x][i]]==0){
            int u=dfs(G[x][i]);
            if(!u)return false;
        }
    }
    vis[x]=1;     //表示访问结束
    topo[--cnt]=x;
}

bool toposort(){
    cnt=N;
    memset(vis,0,sizeof(vis));
    for(int i=1;i<=N;i++)if(vis[i]==0){
        if(dfs(i)==false)return false;
    }
    return true;
}

int main(){
    G[1].push_back(2);
    G[2].push_back(3);
    G[4].push_back(3);
    N=4;
    toposort();
    for(int i=0;i<N;i++)cout<<topo[i]<<' ';
}

两种算法总结： 
对于基于DFS的算法，增加结果集的条件是：顶点的出度为0。这个条件和Kahn算法中入度为0的顶点集合似乎有着异曲同工之妙，Kahn算法不须要检测图是否为DAG，假设图为DAG，那么在入度为0的栈为空之后，图中还存在没有被移除的边，这就说明了图中存在环路。而基于DFS的算法须要首先确定图为DAG，当然也可以做出适当调整，让环路的检测測和拓扑排序同一时候进行，毕竟环路检測也可以在DFS的基础上进行。 
二者的复杂度均为O(V+E)。