Re-Verse Note #1 - Persistent / Luogu P3402 Solution

0. 胡诌

Persistent，意为“持久”。尽管，在编程竞赛中，Persistent 一词与“持久”没有任何关系。它们能沿用“持久”的译名，完全应该归因于那些对如何“翻译”一窍不通的前辈们——当然，我丝毫没有指责这些前辈的意思，因为不可否认的，他们为我国的计算机事业发展做出了不可磨灭的贡献。

为什么我要提到“翻译”？因为，我向来不认为 Robust 应该被翻译成“鲁棒性”，也不认为 Default 应该被翻译成“缺省”。Robust 完全可以被翻译为“稳定性”而非“鲁棒性”，而 Default 也确实可以被翻译为“默认”。他们都比这些“业界肯定”的翻译直白得多，也不至于让外行人完全无法理解。

……

啊，我为什么又要在这里胡诌……

好了。接下来，步入正题。

1. 可持久化

可持久化，在我看来，应该译成“可继承化”，因为在信息竞赛方面，可持久化的表现就是对既有信息的高效继承。这一点在可持久化数据结构的基石——可持久化线段树上体现得尤为明显。

2. 可持久化线段树

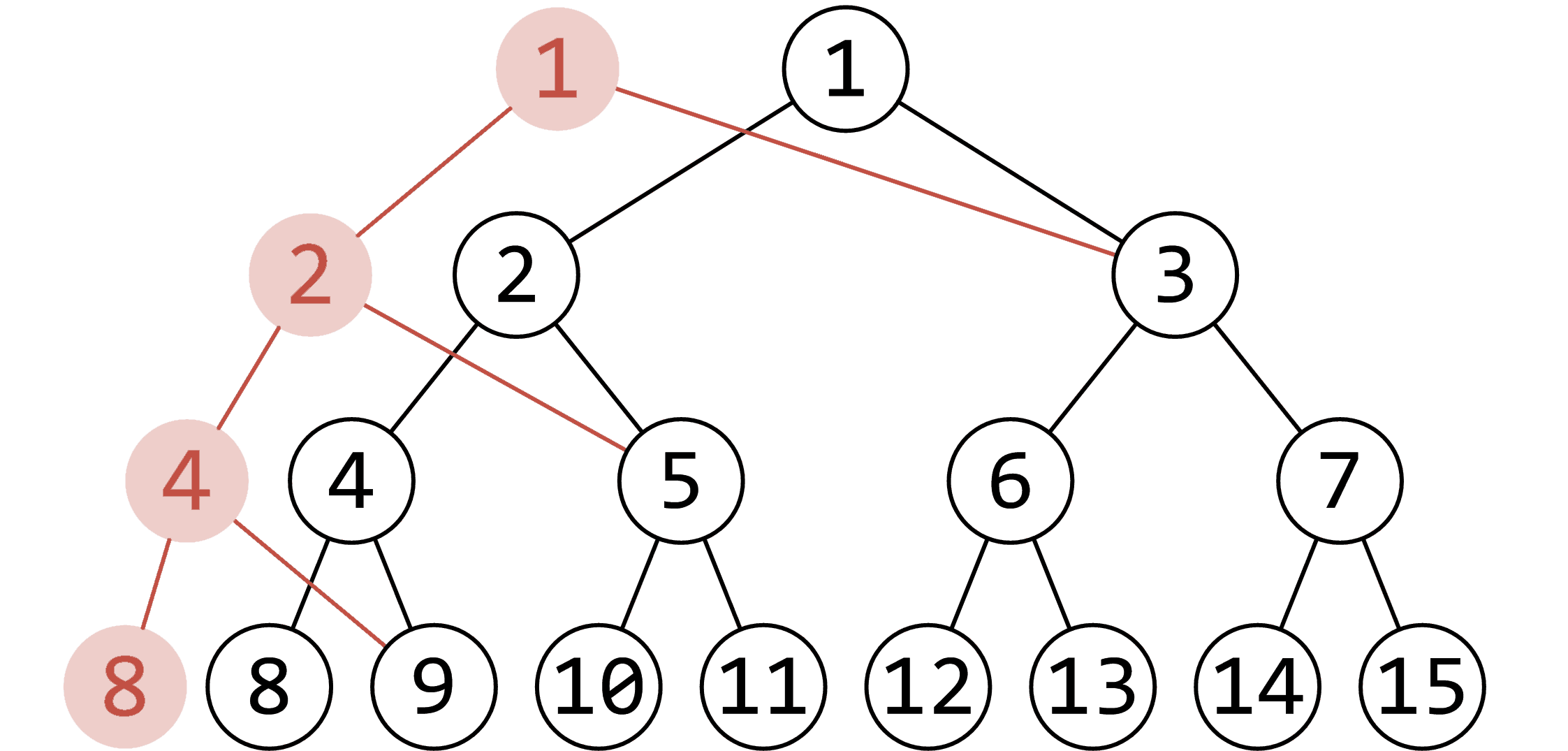
如上图所示，可持久化线段树的性质在于，进行单点修改时，新的线段树只需要新增 \(O(\log n)\) 个节点就可以完成对信息的修改。

它利用了一个性质——我们并不需要将所有的信息复制一遍，因为在原信息不变的情况下，我们大可以直接“引用”原来的数据。

3. 可持久化并查集

可持久化并查集同样需要基于可持久化线段树。一般来说，为了最大化并查集的操作效率，我们会使用路径压缩。这种做法在一般并查集上的确会将时间复杂度降低至 \(O(n\alpha(n))\)，但是一旦将路径压缩搬到可持久化并查集上，大量的节点申请开销会使得程序的内存占用无法接受。所以，我们需要使用一个更加适合可持久化并查集的压缩方法：按秩合并。

这种方法的优化力度并不大，最终的查询复杂度为 \(O(n\log n)\)，但是这种方法每次只需要在额外存储一个连通块大小的前提下对父节点数组进行一次改动，最终的查询/修改的总复杂度为 \(O(n\log^2 n)\)。

所以，这道题就被解决了。

4. 代码

#include <iostream>
using namespace std;
const int N = 2e5 + 10;
int n, m, rt[N], f[N << 6], ls[N << 6], rs[N << 6], idx, siz[N << 6];
void init(int &x, int l, int r)
{
    x = ++idx;
    if (l == r)
    {
        f[x] = l;
        siz[x] = 1;
        return;
    }
    int mid = (l + r) >> 1;
    init(ls[x], l, mid);
    init(rs[x], mid + 1, r);
}
void updatf(int &x, int pre, int l, int r, int tar, int v)
{
    x = ++idx;
    if (l == r)
    {
        f[x] = v;
        siz[x] = siz[pre];
        return;
    }
    int mid = (l + r) >> 1;
    if (tar <= mid)
        updatf(ls[x], ls[pre], l, mid, tar, v), rs[x] = rs[pre];
    else
        updatf(rs[x], rs[pre], mid + 1, r, tar, v), ls[x] = ls[pre];
}
void updats(int &x, int pre, int l, int r, int tar, int v)
{
    x = ++idx;
    if (l == r)
    {
        f[x] = f[pre];
        siz[x] = v;
        return;
    }
    int mid = (l + r) >> 1;
    if (tar <= mid)
        updats(ls[x], ls[pre], l, mid, tar, v), rs[x] = rs[pre];
    else
        updats(rs[x], rs[pre], mid + 1, r, tar, v), ls[x] = ls[pre];
}
int querf(int &x, int l, int r, int tar)
{
    if (l == r)
        return f[x];
    int mid = (l + r) >> 1;
    if (tar <= mid)
        return querf(ls[x], l, mid, tar);
    else
        return querf(rs[x], mid + 1, r, tar);
}
int quers(int &x, int l, int r, int tar)
{
    if (l == r)
        return siz[x];
    int mid = (l + r) >> 1;
    if (tar <= mid)
        return quers(ls[x], l, mid, tar);
    else
        return quers(rs[x], mid + 1, r, tar);
}
int find(int x, int rid)
{
    int tf = querf(rt[rid], 1, n, x);
    if (tf == x)
        return tf;
    return find(tf, rid);
}
void merge(int x, int y, int rid)
{
    x = find(x, rid), y = find(y, rid);
    int tsx = quers(rt[rid], 1, n, x), tsy = quers(rt[rid], 1, n, y);
    if (tsx < tsy)
        swap(x, y);
    updatf(rt[rid], rt[rid], 1, n, y, x);
    updats(rt[rid], rt[rid], 1, n, x, tsx + tsy);
}
int main()
{
    scanf("%d%d", &n, &m);
    init(rt[0], 1, n);
    for (int i = 1, o, x, y; i <= m; i++)
    {
        scanf("%d%d", &o, &x);
        if (o == 2)
        {
            rt[i] = rt[x];
            continue;
        }
        rt[i] = rt[i - 1];
        scanf("%d", &y);
        if (o & 2)
        {
            puts(find(x, i) == find(y, i) ? "1" : "0");
            continue;
        }
        merge(x, y, i);
    }
}