计数专题

AT_agc040_c

应该是一眼题，但我没一眼。考虑一个序列能被删完必定存在一种将 C 替换为 A 或 B 的方式满足只删 AA 和 BB 可以删完，将奇数位置的 A 和 B 翻转，相当于每次删 AB，只需满足 A 数量等于 B 数量即可删完，于是合法序列的条件为 A 和 B 的数量都不是绝对众数，直接计算即可。

AT_agc002_f

容易发现只要任意一个前缀都满足白球数量不小于其他颜色求种类数该序列就是合法的。考虑记 \(f_{i,j} (i \geq j)\) 为当前有 \(i\) 个白球，有 \(j\) 种白球外的颜色的方案数，转移即考虑剩下空位中第一个填白球还是另一种颜色球，分别为 \(f_{i-1,j}\) 和 \(f_{i,j-1} \times \binom{n-i-(k-1)\times (j-1)-1}{k-2} \times (n-j+1)\)，系数为钦定第一个空位填新的颜色球，剩下空位塞 \(k-2\) 个球的方案，再乘上剩余颜色种数。

CF1349D

有一个神秘的鞅与停时定理，可是我不会。

考虑设 \(E_x\) 为游戏结束时所有饼干在 \(x\) 手里的概率乘以期望时间，\(P_x\) 为概率，答案即为 \(\sum_{i=1}^n E_i\)。

设 \(E'_x\) 为只有所有饼干在 \(x\) 手里时游戏才能结束的期望时间，常数 \(C\) 为将所有饼干从一个人手中转到另一人手中的期望时间，那么有 \(E'_x=E_x+\sum_{i\neq x} P_i \times C + E_i\)，注意 \(E_i\) 中已经隐含概率，正确性显然。

推推柿子：

\[E'_x = \sum_{i=1}^n E_i + \sum_{i \neq x} P_i \times C = ans + C \times \sum_{i \neq x} P_i \\ \sum_{x=1}^n E'_x = n \times ans + C \times \sum_{x=1}^n \sum_{i\neq x} P_i = n \times ans + C \times (n-1) \\ ans=\frac{\sum_{i=1}^n E'_i - C \times (n-1)}{n} \]

通过 \(\sum_{i=1}^n E_i = ans\) 以及 \(\sum_{i=1}^n P_i = 1\) 可以得到最终的简化柿子。于是我们只需要算出 \(E'_i\) 和 \(C\) 即可。

设 \(m\) 为饼干总数，\(f_i\) 为一个人拥有 \(i\) 块饼干时所有饼干到他手上的期望时间，容易发现 \(E'_i = f_{a_i},C=f_0\)。

计算 \(f_i\) 是简单的，根据饼干从哪里转到哪里可以推出以下柿子：

\[f_m = 0 \\ f_0 = \frac{n-2}{n-1} \times f_0 + \frac{1}{n-1} \times f_1 + 1 \\ f_i = \frac{i}{m} \times f_{i-1} + \frac{m-i}{m} \times (\frac{n-2}{n-1} \times f_i + \frac{1}{n-1} \times f_{i+1}) + 1 \]

直接转移会出现除 \(0\) 的情况，考虑设 \(g_i = f_i - f_{i+1}\)，那么有：

\[g_0 = \frac{n-2}{n-1} \times g_0 + 1 \\ g_i = \frac{i}{m} \times g_{i-1} + (\frac{i}{m} + \frac{m-i}{m} \times \frac{n-2}{n-1}) \times g_i + 1 \]

化简出来就是：

\[g_0 = n-1 \\ g_i = \frac{(i \times g_{i-1} + m)\times (n-1)}{m-i} \]

递推完做个后缀和即可。

AT_agc019_f

钦定 \(n \geq m\)。

直觉上应该哪个答案多回答哪个，一样的话钦定回答 Yes，初始在网格右上角，对于一个点表示当前剩余两种答案数量，线段表示当前点决策，往左为 Yes，往下为 No，可以画出以下图片（盗的小粉兔图）。

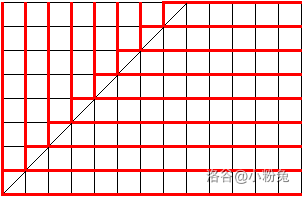
于是对于一个答案序列也能画出一条折线，重合部分长度即为正确数量。考虑任意一条折线，将在斜线上方的部分翻到斜线下方，算少的部分只有在与斜线重合的点并且此时答案为 Yes，而对于一条始终处于斜线下方的折线，答案必定为 \(n\)，于是最终答案即为 \(n \times \binom{n+m}{n}\) 加上对于斜线上每个点，经过该点的折线方案数乘上期望 \(\frac 1 2\) 的贡献，最后由于算的是期望，所以除以 \(\binom{n+m}{n}\)。

P10008

考虑一个 \(b\) 如何映射到一个能生成出来这个 \(b\) 的 \(a\)，策略即为从大到小加入 \(b\)，将没染色的位置染为 \(b_i\)，最后将所有没染色的位置染为 \(1\)。我们对于这样的 \(a\) 计数。

考虑 \(f_{l,r,i}\) 表示 \(a_{l \sim r}\) 均大于等于 \(i\) 的方案数，转移考虑第一个 \(i\) 的出现位置，具体查看洛谷题解。

由于转移式都是简单加乘，所以最终的 \(f_{1,n}\) 是一个 \(O(n)\) 次的多项式，拉插即可。

P10004

考虑二元二项式反演 \(f_{i,j} = \sum_{a\geq i}\sum_{b\geq j}\binom{a}{i}\binom{b}{j} g_{i,j}\) 有 \(g_{i,j} = \sum_{a\geq i}\sum_{b\geq j}(-1)^{a-i}(-1)^{b-j}\binom{a}{i}\binom{b}{j} f_{i,j}\)，容易优化到 \(O(n^3)\)。

考虑钦定此时排列的相邻上升对有 \(x\) 个，逆排列的相邻上升对有 \(y\) 个，最后二元二项式反演算出答案。此时排列中有 \(n-x\) 个连续上升段，逆排列中有 \(n-y\) 个连续上升段，设 \(c_{i,j}\) 为排列中第 \(i\) 个上升段在逆排列的第 \(j\) 个上升段中有多少个，将 \(c_{i,j}\) 写为矩阵，那么合法矩阵条件即为每个元素为非负数，每行每列的和大于 \(0\)，且矩阵中的数总和为 \(n\)，正确性根据排列中的连续上升段在逆排列中的顺序关系仔细想想就能明白。

考虑只满足非负数以及矩阵中的数总和为 \(n\) 这一条件，方案数为 \(\binom{n+xy-1}{xy-1}\)，再次使用二元二项式反演钦定有多少行和列的和为 \(0\) 算出答案即可。