大数据分析:疫情分析
此项目为《大数据分析》的期末作业,分为四个任务,四个任务所用的covid都是源数据covid-19-all.csv的pandas对象。本文的数据预测使用的是python的机器学习sklearn中的指数平滑法,使用方式比较粗糙,只是用来应付期末作业要求,来源是csdn博客文章,希望大佬们轻点喷QAQ。
任务1:依据地区的最新数据,进行确诊、治愈和死亡人数三项数据的描述统计
import json import jieba import pandas as pd from pandas import Series,DataFrame import Numpy as np from datetime import datetime import matplotlib.pyplot as plt import seaborn as sns %matplotlib inline plt.rcParams['font.sans-serif']=['SimHei'] plt.rcParams['axes.unicode_minus']=False
从本地中读取COVID-19数据文件,同时检查数据之后发现一些数据存在空值,主要是中国地区在疫情刚发生的前几天中缺少治愈人数或死亡人数数据,同时一些国家只有地区名,没有行政区,所以用0填充,便于分析。这里把地区的空值也用0填充了,本来是不对的,但是不影响分析,所以不加以修改。
covid = pd.read_csv('../../covid-19-all.csv') covid.fillna(0,inplace=True) covid
执行结果如下图:
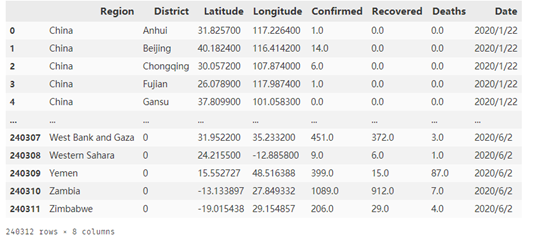
根据题目要求,接下来提取2020年6月2日,即最新的疫情数据,并进行统计。(这里也可以考虑用max聚合函数提取最新的数据)
1 covidnewest = covid[covid['Date'] == '2020/6/2'] 2 covidnewest = covidnewest.groupby('Region')['Confirmed','Recovered','Deaths'].sum() 3 covidnewest = covidnewest.sort_values(by = ['Confirmed','Recovered','Deaths'],ascending=False).head(20) 4 covidnewest
选取日期为6月2日的数据之后,用地区作为依据,对数据进行分组,同时将各个日期上的数据进行求和计算。由于国家数量过多,这里只选取前20个国家。以上代码执行的结果如下图所示。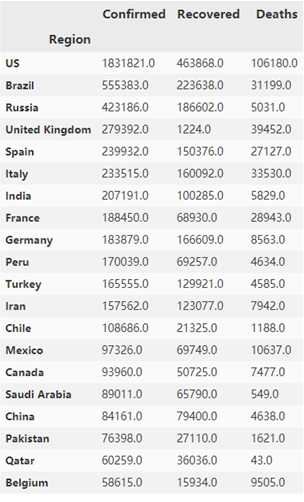

接下来用covidnewest进行绘图。用Region作为x轴的标签,同时调整x轴、y轴、以及图例的字体大小.
covidnewest.plot(kind='bar',figsize=(20,15)) plt.xlabel('Region',fontsize=30) plt.xticks(fontsize=20,rotation=40) plt.yticks(fontsize=20) plt.legend(fontsize=30)
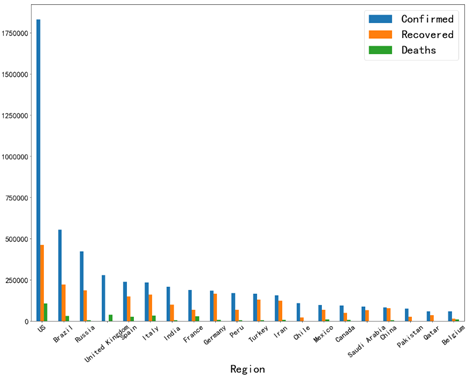
从上图可以看出,全球疫情情况最严重的是美国,截止至6月2日累计确诊人数已经达到180万,同时治愈与死亡人数也高居世界第一位。而巴西、俄罗斯、英国等国家紧随其后,疫情形势仍然较为严峻。
任务2:依据地区的最新三项数据,进行数据的地图呈现
首先先对数据进行筛选,先从原数据中选出日期为2020年6月2日的数据,再使用grouby()通过Region分组,分别筛选出全世界各个国家的确认人数、死亡人数、治愈人数的数据,分别存在三个不同的表中。
covidnewest2 = covid[covid['Date']=='2020/6/2'] confirmed = covidnewest2[['Region','Confirmed']].groupby('Region').sum() recovered = covidnewest2[['Region','Recovered']].groupby('Region').sum() deaths = covidnewest2[['Region','Deaths']].groupby('Region').sum() confirmed.to_excel('confirmed.xlsx') recovered.to_excel('recovered.xlsx') deaths.to_excel('deaths.xlsx') confirmed2 = pd.read_excel('confirmed.xlsx') recovered2 = pd.read_excel('recovered.xlsx') deaths2 = pd.read_excel('deaths.xlsx')
confirmed2,recoverd2,deaths2的数据情况分别如下图所示:
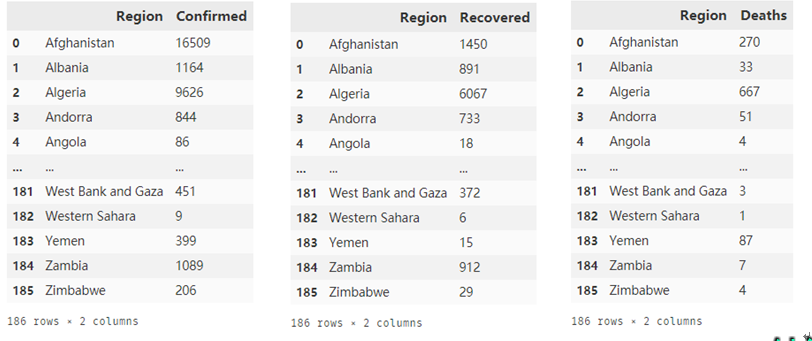
同时注意到表中的美国的英文名称为”US”,而在pyecharts中美国的默认名称是为”United States”,所以这里先把三个表中的美国名称进行修改:
confirmed2.loc[confirmed2.Region == 'US','Region'] = 'United States' recovered2.loc[confirmed2.Region == 'US','Region'] = 'United States' deaths.loc[confirmed2.Region == 'US','Region'] = 'United States'
下面分别对三个表进行pyecharts的世界地图绘制,首先要导入pyecharts第三方库,然后对参数进行调整:
from pyecharts import Map attr1 = confirmed2['Region'] attr2 = recovered2['Region'] attr3 = deaths2['Region'] v1 = confirmed2['Confirmed'] v2 = recovered2['Recovered'] v3 = deaths2['Deaths'] map=Map("世界疫情确诊人数",width=1200,height=700) map.add("",attr1,v1,maptype="world",is_visualmap=True,visual_text_color="black") map.render("confirmed.html") map=Map("世界疫情治愈人数",width=1200,height=700) map.add("",attr2,v2,maptype="world",is_visualmap=True,visual_text_color="black") map.render("recovered.html") map=Map("世界疫情死亡人数",width=1200,height=700) map.add("",attr3,v3,maptype="world",is_visualmap=True,visual_text_color="black") map.render("deaths.html")
结果如下三张图所示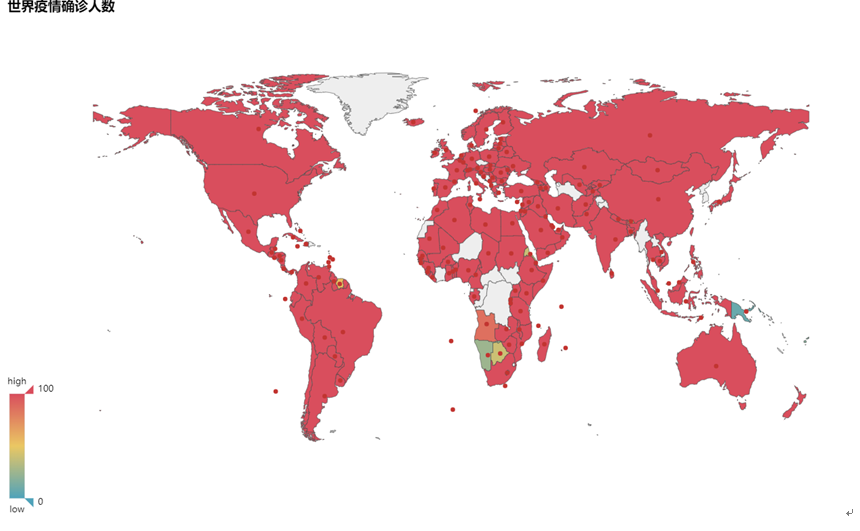
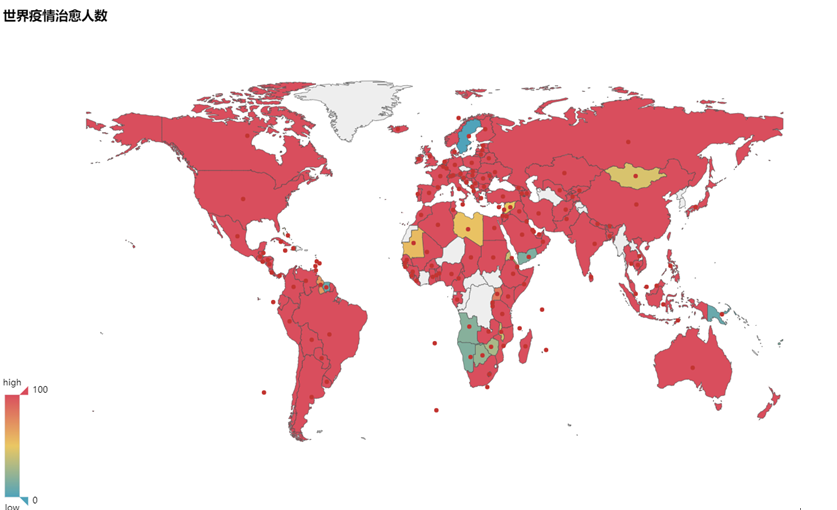
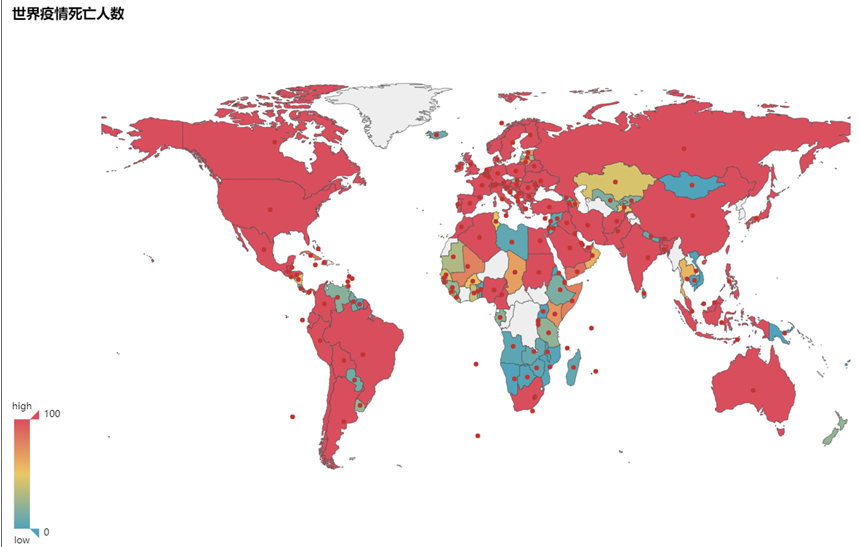
从如上三张图可以得知,世界各国的疫情防控仍然不容乐观,尤其是美国,形势尤为严峻,各项数据高居世界第一位,而欧洲各国的数据也在世界前列,形势也较为严峻。但是中国的疫情严重程度已经降低,但是仍不能小视。
任务3:依据地区的三项数据,进行周期为7天的数据预测
先对数据进行整理,因为Confirmed, Recovered , Deaths三项数据存在空值,所以用0填充;然后对数据groupby聚合,根据地区和时间进行分组。
1 covid = pd.read_csv('covid-19-all.csv') 2 covid['Confirmed'].fillna(0,inplace=True) 3 covid['Recovered'].fillna(0,inplace=True) 4 covid['Deaths'].fillna(0,inplace=True) 5 6 #根据Region和Date进行聚合 7 covid = covid[['Region','Confirmed','Recovered','Deaths','Date']].groupby(['Region','Date']).sum() 8 covid.to_excel('covidgb.xlsx') 9 covid2 = pd.read_excel('covidgb.xlsx') 10 covid2.fillna(method = 'ffill' , inplace = True) 11 covid2
上面的代码执行的结果如下左图所示,而covid2的dtypes如右下图所示:
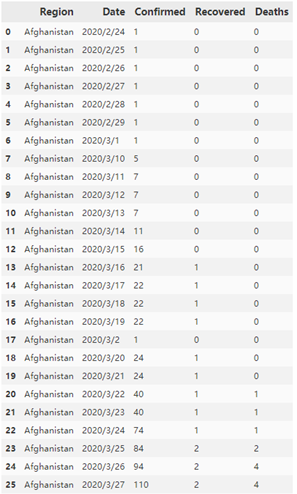
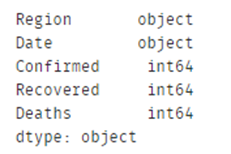
不难发现,上图中,第7行日期为2020/3/1,第8行的日期直接跳到2020/3/10,所以要考虑根据日期进行排序;同时注意到日期Date的数据类型是object,要转换成datetime类型:
#将Date的数据类型转换为datetime covid2['Date'] = pd.to_datetime(covid2['Date'], format='%Y/%m/%d').values.astype('datetime64[h]') covid2.sort_values(by='Date',inplace = True) covid2.to_excel('covidgbv4.xlsx') covid2.head(20)
以上代码的执行结果如下图,因为此处国家的顺序被打乱,所以接下来在进行数据预测的时候要把国家分别提取。
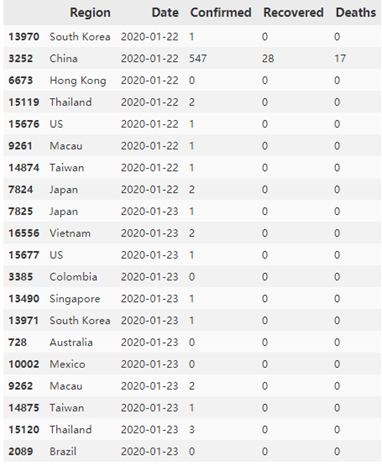
由于国家数量众多,这里分别选取中国和美国的疫情数据查看变化趋势。
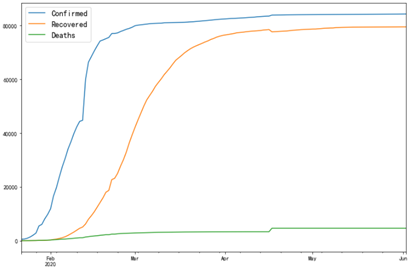
1 china = covid2[covid2['Region'] == 'China'] 2 china.index = pd.Index(pd.date_range('2020-01-22','2020-06-02',freq = '1D')) 3 china['Confirmed'].plot(figsize = (12,8)) 4 china['Recovered'].plot(figsize = (12,8)) 5 china['Deaths'].plot(figsize = (12,8)) 6 plt.legend(fontsize = 14) 7 plt.show()
us = covid2[covid2['Region'] == 'US'] us.index = pd.Index(pd.date_range('2020-01-22','2020-06-02',freq = '1D')) us['Confirmed'].plot(figsize = (12,8)) us['Recovered'].plot(figsize = (12,8)) us['Deaths'].plot(figsize = (12,8)) plt.legend(fontsize = 14) plt.show()
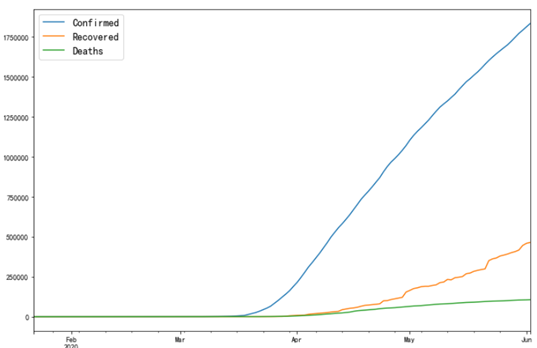
从上面两张图我们可以看到,中国和美国的疫情形势发展呈现不同的趋势,中国在短时间内逐渐增长至峰值,然后趋于平稳,而美国的确诊人数随着时间推移呈线性增长趋势不断上升,但是增长率也存在下降的趋势,两个国家的疫情数据都随着时间伴随着一定的特征,且时间的连续性比较好,所以以下采用时间序列分析的方式。由于国家数目众多,这里只针对美国与中国的数据进行预测将所有数据分成两部分,训练集为2020-05-26及以前的数据,测试集为2020-05-27以后的数据,测试集的时间维度为2020-05-27到2020-06-02,长度为7天,然后利用指数平滑模型(Holt_Winter)对训练集进行学习,然后用测试集进行评估。首先对中国的疫情数据进行预测,先选取测试集和训练集:
train_china = china[china['Date']<'2020-05-27'] test_china = china[china['Date']>='2020-05-27']
train_china和test_china分别如下左右图所示:

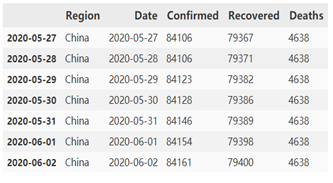
导入所需要的库,其中mean_squared_error用于计算均方根误差,ExponentialSmoothing用于指数平滑预测。
from sklearn.metrics import mean_squared_error from math import sqrt from statsmodels.tsa.api import ExponentialSmoothing
接下来对中国的数据进行预测,先复制一份进行实验,然后利用指数平滑的模型进行预测,调整参数,由于疫情只发生在今年的春夏季,所以季节性影响不大,在ExponentialSmoothing()方法的seasonal参数设置为None。先对中国的数据进行预测。
china_avg = test_china.copy() fit1 = ExponentialSmoothing(np.asarray(train_china['Confirmed']), trend='add', seasonal=None ).fit() fit2 = ExponentialSmoothing(np.asarray(train_china['Recovered']), trend='add', seasonal=None ).fit() fit3 = ExponentialSmoothing(np.asarray(train_china['Deaths']), trend='add', seasonal=None ).fit() china_avg['Holt_Winter_Confirmed'] = fit1.forecast(len(test_china)) china_avg['Holt_Winter_Recovered'] = fit2.forecast(len(test_china)) china_avg['Holt_Winter_Deaths'] = fit3.forecast(len(test_china)) china_avg
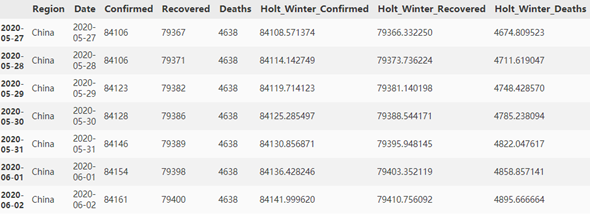
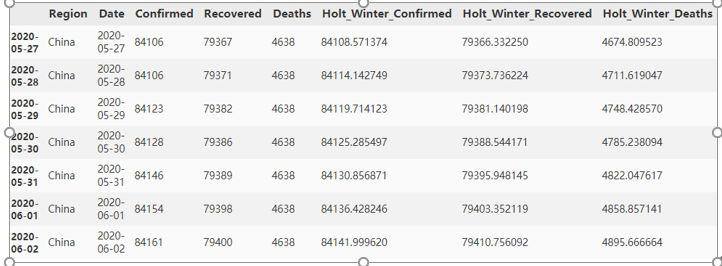
对预测结果和实际的test_china数据进行对比,可以看出,Confirmed, Recovered, Deaths三项数据的预测结果与实际情况的契合程度相对不错,接下来对预测结果计算均方根误差:
rms1 = sqrt(mean_squared_error(test_china['Confirmed'], china_avg['Holt_Winter_Confirmed'])) rms2 = sqrt(mean_squared_error(test_china['Recovered'], china_avg['Holt_Winter_Recovered'])) rms3 = sqrt(mean_squared_error(test_china['Deaths'], china_avg['Holt_Winter_Deaths'])) print('The mean squared error of Confirmed is : ' + str(rms1)) print('The mean squared error of Recovered is : ' + str(rms2)) print('The mean squared error of Deaths is : ' + str(rms3))

可以看出,对于confirmed、recovered的数据,均方根误差相对较小,预测的结果较为准确,而Deaths的数据均方根误差相对较大,预测结果准确性相对较低。对于中国疫情数据使用指数平滑法预测的效果相对较好。接下来对美国数据进行预测。
train_us = us[:'2020-05-26 '] test_us = us['2020-05-27':]
train_us和test_us分别如下左右图所示
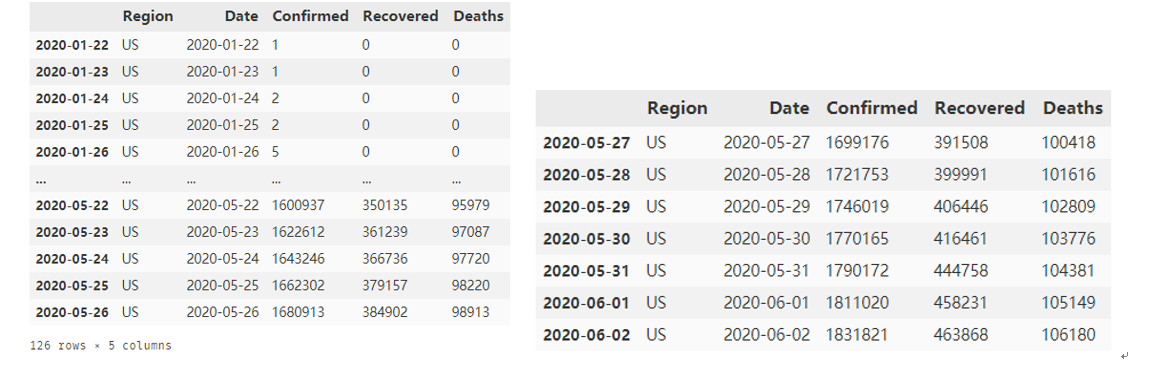
与中国疫情数据的预测类似,采用指数平滑法进行分析:
us_avg = test_us.copy() fit1 = ExponentialSmoothing(np.asarray(train_us['Confirmed']), trend='add', seasonal=None ).fit() fit2 = ExponentialSmoothing(np.asarray(train_us['Recovered']), trend='add', seasonal=None ).fit() fit3 = ExponentialSmoothing(np.asarray(train_us['Deaths']), trend='add', seasonal=None ).fit() us_avg['Holt_Winter_Confirmed'] = fit1.forecast(len(test_china)) us_avg['Holt_Winter_Recovered'] = fit2.forecast(len(test_china)) us_avg['Holt_Winter_Deaths'] = fit3.forecast(len(test_china)) us_avg
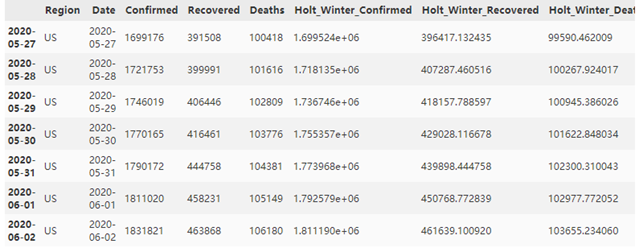
对预测结果和实际的test_us数据进行对比,可以看出,Confirmed, Recovered, Deaths三项数据的预测结果与实际情况的契合程度相对不错,接下来对预测结果计算均方根误差:
rms1 = sqrt(mean_squared_error(test_china['Confirmed'], us_avg['Holt_Winter_Confirmed'])) rms2 = sqrt(mean_squared_error(test_china['Recovered'], us_avg['Holt_Winter_Recovered'])) rms3 = sqrt(mean_squared_error(test_china['Deaths'], us_avg['Holt_Winter_Deaths'])) print('The mean squared error of Confirmed is : ' + str(rms1)) print('The mean squared error of Recovered is : ' + str(rms2)) print('The mean squared error of Deaths is : ' + str(rms3))
结果如下图:

可以看出,对于Confirmed、Recovered、Deaths的数据均方差较大,预测结果与实际差距可能较大,可能是由于美国疫情形势较为复杂,用指数平滑法的预测效果相对较差,也有可能是方法使用错误,还需要进一步学习。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号