SGU435 UFO Circles 题解

题目链接

题目简意

给出平面直角坐标系中若干个互不相同的圆，分别求出求被这些圆覆盖奇数次的区域的面积和覆盖偶数次（至少一次）的区域的面积。$n\le 100,|x_i|,|y_i|,r_i\le 1000$

题解

前置知识 ：格林公式

大学里面微积分里面的内容，这里我们直接讲结论不讲证明（其实是我不是很懂微积分，并不会证，下面讲的内容凭我个人理解，不保证严谨正确），有兴趣的同学可以继续看，其他同学可以直接下翻到格林公式在 OI 里的应用。

格林公式：设闭区域 $D$ 由分段光滑的曲线 $L$ 围成，函数 $P(x,y)$ 和 $Q(x,y)$ 在 $D$ 上具有一阶连续偏导数，则有：

$$\underset{D}{\iint }(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})\text{d}x\text{d}y={\oint }_{L}P\text{d}x+Q\text{d}y$$

看不懂没关系，大概解释一下它讲了个啥。首先对于闭区域 $D$ ，我们要求它里面没有 “洞”，如果有的话，减一减就好了。其次，上面这个公式其实是可以对 $P(x,y)$ 和 $Q(x,y)$ 分别写的，不过应用中一般都有，所以通常写在一起。然后左边的是一个二重积分，和普通的积分是一样的，只不过把坐标系变成了三维的，如果你把一重的定积分理解成有向面积，那么二重的定积分就是有向体积（应该很好理解吧）。$\frac{\partial Q}{\partial x}$ 是对 $x$ 求偏导，相当于把 $y$ 看成常数，对 $x$ 求导，$\frac{\partial P}{\partial y}$ 也是一个道理。右边是一个对闭合曲线求对坐标的曲线积分，也就是第二类曲线积分，这个我不是很懂，不过你可以理解成一个变力绕着曲线 $L$ 做功。

在 OI 中，格林公式常用于求解圆形面积并。我们令 $P(x,y)=-y,Q(x,y)=x$，就可以得到：

$$2\underset{D}{\iint }\text{d}x\text{d}y={\oint }_{L}x\text{d}y-y\text{d}x$$

左边那坨不就是区域 $D$ 面积的两倍吗，假设它的面积是 $A$，那么就有：

$$A=\frac{1}{2}{\oint }_{L}x\text{d}y-y\text{d}x$$

考虑一个圆心坐标为 $(x_0,y_0)$，半径为 $r$ 的圆。写出它的参数方程：

$$\{\begin{array}{l}x=x_0+r\cos \theta \\ \\ y=y_0+r\sin \theta \end{array}\alpha \le \theta \le \beta$$

直接带到公式里面去：

$$\begin{array}{rl}A& =\frac{1}{2}{\oint }_L(x_0+r\cos \theta )\text{d}(y_0+r\sin \theta )-(y_0+r\sin \theta )\text{d}(x_0+r\cos \theta )\\ \\ & =r(x_0\sin \theta -y_{0}cos\theta +r\theta ){|}_{\alpha }^{\beta }\\ \\ & =r(x_0\sin \beta -y_{0}cos\beta +r\beta )-r(x_0\sin \alpha -y_{0}cos\alpha +r\alpha )\end{array}$$

积分的推导过程省略了（其实还是我不是很懂），$\alpha$ 和 $\beta$ 是 $L$ 的参数方程中的起点和终点对应的参数，如果 $L$ 是圆的话，可以令 $\beta -\alpha =2\pi$ ，如果 $L$ 是一段圆弧的话，把 $\alpha$ 和 $\beta$ 带成端点出的极角即可，注意一定要保证 $\alpha \le \beta$ 。

最后得到的这个公式告诉我们，在求圆形面积并的时候只需要关心组成圆形并的轮廓的那些圆弧的参数，对于每一段弧，带入公式求出答案，全部加起来就是圆形面积并。至于那些圆弧怎么求，下面再讲。

回归本题

这个问题有点类似圆形面积并，因为第一问的答案加第二问的答案就是圆形面积并，我们考虑使用格林公式解决这个问题。画几个图可以发现一个重要的性质：被覆盖了 $x$ 次的区域的边界是由被其他圆覆盖了 $x-1$ 次和 $x$ 次的圆弧围成的。

举个例子：

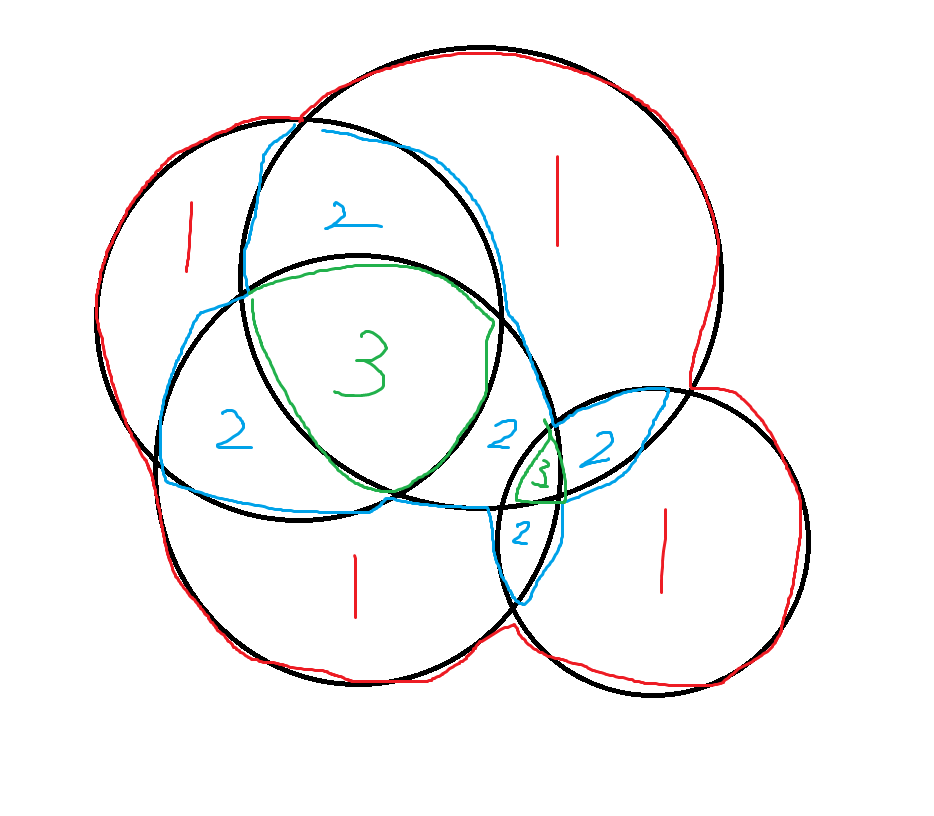
红色/蓝色/绿色标注的弧是被其他圆覆盖 $0/1/2$ 次的弧。使用归纳法不难证明这个结论。

再稍微把这个结论转化一下：至少被覆盖了 $x$ 次的区域的边界是由被其他圆覆盖了 $x-1$ 次的圆弧围成的 。这显然也是对的，设 $S_x$ 是至少被覆盖了 $x$ 次的区域的面积，那么恰好被覆盖了 $x$ 次的区域的面积就是 $S_x-S_{x+1}$，所以我们只需要求出 $S_x$ ，求能求出恰好被覆盖了 $x$ 次的区域的面积，那么覆盖了奇数次的和偶数次的面积就迎刃而解了。

对于 $S_x$ ，我们找到所有被其他圆覆盖了 $x-1$ 次的圆弧，求出它们的参数，再用格林公式计算面积即可。求一段圆弧被覆盖了多少次是一个经典问题，考虑枚举中心圆，再枚举覆盖了它的圆，利用一些几何知识便可以得到中心圆被覆盖的圆弧。显然一个圆最多覆盖中心圆的一段圆弧，所以圆上覆盖次数不同的点最多只有 $\mathcal{O}(n)$ 个，离散化之后差分计算即可。这样子就可以得到所有弧被覆盖了几次，用格林公式贡献给对应的 $S_x$ 即可。

举个例子，假设中心圆是上面那张图右下角的圆，那么发现它左边的圆和上面的圆都会覆盖到它的一部分圆弧，形成了覆盖次数分别是 $1,2,1,0$ ，把这四段圆弧用格林公式分别贡献给 $S_2,S_3,S_2,S_1$ 即可。

时间复杂度 $\mathcal{O}(n^2\log n)$ 。

实际上，圆形面积并求的就是 $S_1$ 。

代码

#include <bits/stdc++.h>
#define re(i, x, y) for (int i = (x); i < (y); ++i)
#define rep(i, x, y) for (int i = (x); i <= (y); ++i)

using namespace std;
using db = long double;

const db pi = acosl(-1.0), eps = 1e-12;
int n, m;
int d[205];
db ky[205], S[105];
pair<db, db> arc[205];
struct circ {
    int x, y, r;
} a[105];

db f(circ c, db th) { // 格林公式
    return c.r * (c.x * sinl(th) - c.y * cosl(th) + c.r * th);
}

int main() {
#ifdef sword
    freopen("test.in", "r", stdin);
#endif

    scanf("%d", &n);
    rep(i, 1, n) {
        scanf("%d%d%d", &a[i].x, &a[i].y, &a[i].r);
    }
    rep(i, 1, n) {
        int cov = 0, t = 0, k = 0;
        ky[++k] = -pi, ky[++k] = pi;
        rep(j, 1, n) {
            if (i == j) {
                continue;
            }
            db d = hypotl(a[i].x - a[j].x, a[i].y - a[j].y);
            if (d >= a[i].r + a[j].r) {
                continue;
            }
            if (a[i].r + d <= a[j].r) {
                ++cov; // 注意一个圆完全被另一个圆包含
                continue;
            }
            if (a[j].r + d <= a[i].r) {
                continue;
            }
            db th = atan2l(a[j].y - a[i].y, a[j].x - a[i].x), de = acosl((a[i].r * a[i].r + d * d - a[j].r * a[j].r) / 2 / a[i].r / d);
            db l = th - de, r = th + de;
            if (r > pi) {
                r -= 2 * pi;
            }
            if (l - eps < -pi) {
                l += 2 * pi;
            }
            ky[++k] = l, ky[++k] = r;
            if (l <= r) {
                arc[++t] = make_pair(l, r);
            }
            else {
                arc[++t] = make_pair(l, pi);
                arc[++t] = make_pair(-pi, r);
            }
        }
        sort(ky + 1, ky + k + 1);
        k = unique(ky + 1, ky + k + 1) - ky - 1;
        memset(d, 0, sizeof(d));
        rep(j, 1, t) {
            int l = lower_bound(ky + 1, ky + k + 1, arc[j].first) - ky, r = lower_bound(ky + 1, ky + k + 1, arc[j].second) - ky;
            ++d[l], --d[r];
        }
        re(j, 1, k) {
            d[j] += d[j - 1];
            S[cov + d[j]] += f(a[i], ky[j + 1]) - f(a[i], ky[j]);
        }
    }
    db a1 = 0, a2 = 0;
    re(i, 0, n) {
        S[i] -= S[i + 1];
        (i & 1 ? a2 : a1) += S[i];
    }
    printf("%.6Lf %.6Lf\n", a1 / 2, a2 / 2); // 把 1/2 提出来最后算
    return 0;
}