第三次软件工程作业

软件工程第三次作业

最大子段和的优化和测试分析

---

题目(1)：最大连续子数组和（最大子段和）
背景

 问题： 给定n个整数（可能为负数）组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0，依此定义，所求的最优值为： Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如，当（a[1],a[2],a[3],a[4],a[5],a[6]）=(-2,11,-4,13,-5,-2)时，最大子段和为20。
-- 引用自《百度百科》

---

• 简单说一下这个问题的历史出处：该问题最初由布朗大学的Ulf Grenander教授于1977年提出，当初他为了展示数字图像中一个简单的最大似然估计模型。不久之后卡内基梅隆大学的Jay Kadane提出了该问题的线性算法。（Bentley 1984）详见资料链接（https://en.wikipedia.org/wiki/Maximum_subarray_problem）

• 最大子列和问题并不鲜见，本人也并非现在才涉及到这个问题，早在大一学期培训期间的一本算法书（《算法竞赛入门经典》（第二版））竞赛篇中就略知一二，还记得当初只会暴力求解（扎心的三重For循环啊！）的我从中感受到了多么大的鼓励和感动。其次还能提到的另一本举世经典之作《算法导论》（第三版）也涉及到了该问题的解决之法 -详见（第四章-分治策略-第4.1小节-最大子数组问题），该问题由如何确定股票的买进和卖出日期来实现最大化利益引申而来。如下：很显然这种枚举算法时间复杂度T（n）=O(n的三次幂)，其次优化的分治法的效率是O（nlgn）我们这里带过不提,最后要提到的是其效率为O（N）的最优算法动态规划。

• 三重for循环的暴力求解（该源码来自《算法竞赛入门经典》一书）

tot = 0;
best = A[1];//初始化最大值
for(int i=1;i<=n;i++)
for(int j=i;j<=n;j++){//检查连续子序列A[i]-A[j]
int sum=0;
for(int k=i;k<=j;k++){sum+=A[k];tot++;}//累加元素和
if(sum>best)best=sum;//更新最大值
}

• 分治法求解的伪代码（毕竟还没有彻底掌握该算法，所以只能给出以下伪代码示例）

算法MaxSubSum(A,left,right)
数组A,left,right为左右界
1.if|A| =1 then 输出元素（值为负输出零）
2.其中得到的累加小于0的子列和都记为零
3.center <——【（left+right）/2】
4.leftsum<——MaxSubSum(A,left,center)
5.rightsum<——MaxSubSum（A，center+1,right）
6.S1<——A1[center]
7.S2<——A2[center+1]
8.sum<——S1+S2
9.if leftsum>sum then sum<——leftsum
10.if rightsum>sum then sum<——rightsum

• 动态规划求解方法（下面为源代码可以运行）

public class Maximum {
	
	public static int maxSubSum(int[] a){
	 
	int maxSum = 0; 
	int tempSum = 0;//临时最大子数列和
	int begin = 0;
	for(int i = 0; i<a.length; i++){
		if(tempSum > 0)
			tempSum += a[i];
		else
		{
			tempSum =a[i];
			begin = i;
		}
		if(tempSum > maxSum){
			maxSum = tempSum;
		}
	}
	return maxSum;	
}
}

下面对动态规划法做主要分析测试

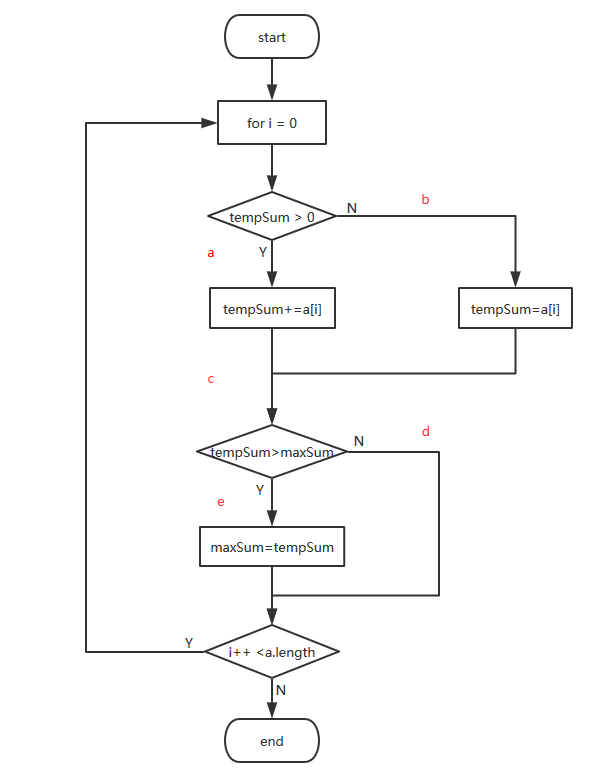
• 程序执行框图如下：
  

• 选择判定/条件覆盖方法对标准设计测试用例
  即设计足够的测试用例，得使判断中每个条件的所有可能取值至少执行一次，同时每个判断本身所有可能结果也至少执行一次
  该算法的每个条件组合共四个分别为：路径ace、acd、bcd、bce(由流程图可得到)；所有判断可能结果有六种：tempsum大于或等于或小于零，tempsum大于或等于或小于maxSum。测试用例1能满足该覆盖所有的条件（由下图表可知）
  记tempsum为T，maxsum为M

测试用例1| -2 | 11|-4|13|-5|-2

• | -: | -: | -: | -: | -: | -: |
  条件路径 | bcd| bce|acd|ace|acd|acd
  判断1结果|T=0 | T<0 | T>0 | T>0 | T>0| T>0
  判断2结果|T等于M|T小于M |T大于M |T等于M|T大于M| T大于M

测试用例2|1|-3|7|8|-4|12|-10|6

• | -: | -: | -: | -: | -: | -: | -: | -: |
  条件路径 |bce|acd|bce|ace|acd|ace|acd|acd
  判断1结果|T=0 | T>0|T>0|T>0|T>0|T>0|T>0|T>0
  判断2结果|T等于M|T等于M|T小于M|T等于M|T等于M|T小于M|T等于M|T小于M

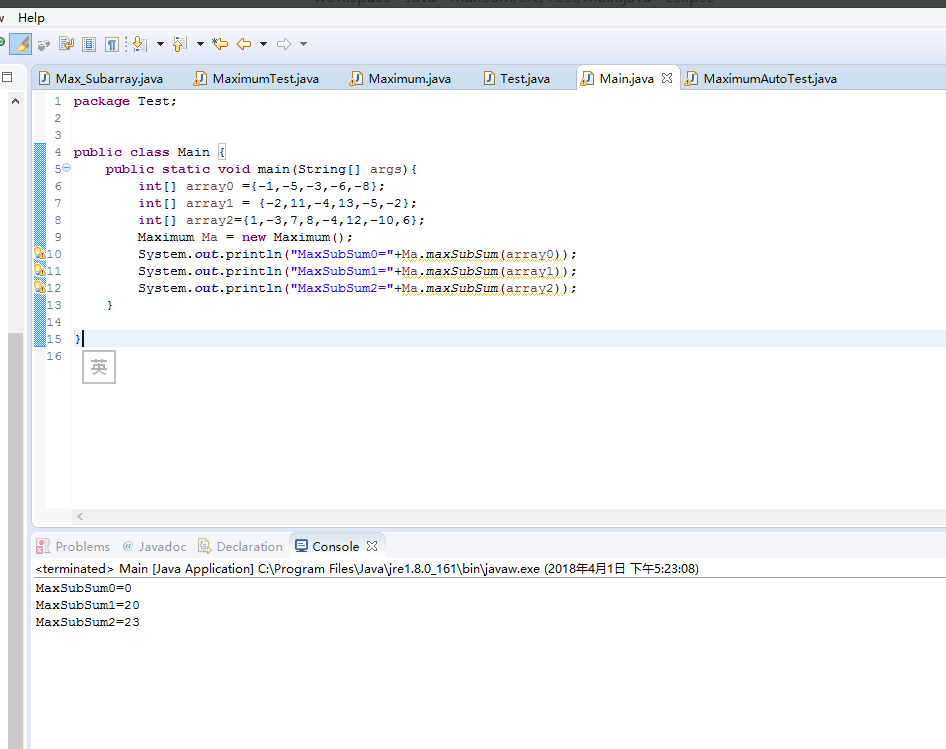
• 程序运行结果图 如下：
  

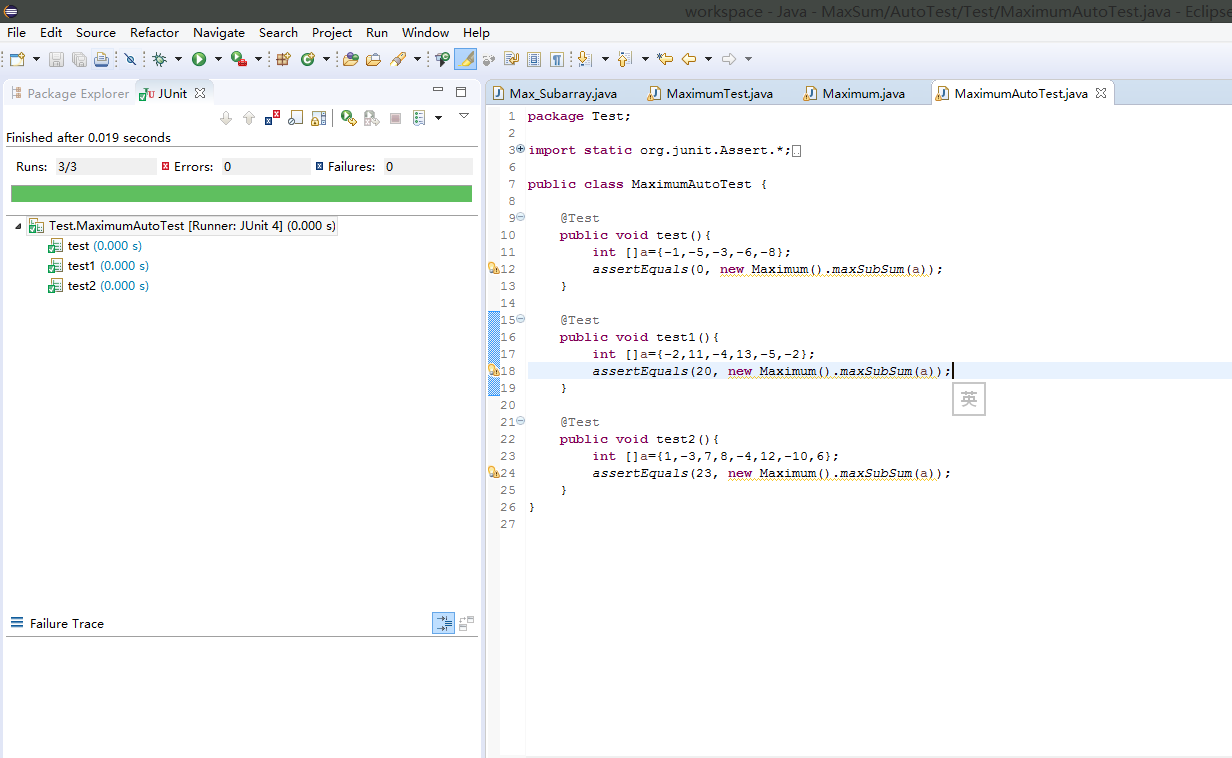
• 自动单元测试结果图如下：
  
  附上[代码地址] (https://github.com/supremexiongxing/project）

引用

• 《算法导论》（原书第3版）机械工业出版社 (美)Thomas H.Cormen Charles E.Leiserson 著
• 《算法竞赛入门经典》（第二版）》清华大学出版社 刘汝佳 编著

外部链接：

• https://en.wikipedia.org/wiki/Maximum_subarray_problem

• https://www.geeksforgeeks.org/largest-sum-contiguous-subarray/