浙大《数据结构》第五章:树(下)
注:本文使用的网课资源为中国大学MOOC
https://www.icourse163.org/course/ZJU-93001
堆(heap)
优先队列(priority queue):特殊的队列,取出元素的顺序是依照元素的优先权(关键字大小),而不是元素进入队列的先后顺序.
此时,可以用完全二叉树表示优先队列
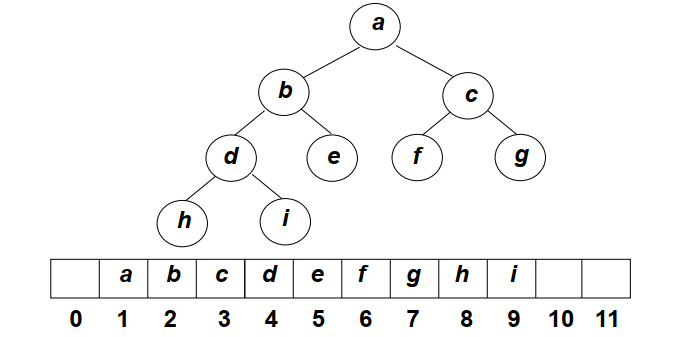
堆的两个特性:
结构性:用数组表示的完全二叉树;
有序性:任意结点的关键字是其子树所有结点的最大值或者最小值。
- 最大堆(MaxHeap),也称“大顶堆”:最大值;
- 最小堆(MinHeap),也称“小顶堆”:最小值
56 21 5 17
/ \ / / \ / \
19 40 10 16 30 19 30
/ \ / / \ / /
18 9 3 49 18 38 33
最大堆 最大堆 最小堆 最小堆
堆的抽象数据类型描述
类型名称:最大堆(MaxHeap)
数据对象集:完全二叉树,每个结点的元素值不小于其子结点的元素值。
操作集:最大堆\(H \in MaxHeap\),元素\(item \in ElementType\),主要操作有:
MaxHeap Create( int MaxSize); // 创建一个空的最大堆
Boolean IsFull( MaxHeap H ); // 判断最大堆H是否已满
Insert( MaxHeap H, ElementType item ); // 将元素item插入最大堆H
Boolean IsEmpty( MaxHeap H ); // 判断最大堆H是否为空
ElementType DeleteMax( MaxHeap H ); // 返回H中最大元素(高优先级)
最大堆的操作
#define MaxData 100000
typedef int ElementType;
typedef struct HeapStruct *MaxHeap;
struct HeapStruct
{
ElementType *Elements; // 存储堆元素的数组
int Size; // 堆的当前元素个数
int Capacity; // 堆的最大容量
};
/* 判断堆是否已满 */
bool IsFull( MaxHeap H )
{
return (H->Size == H->Capacity);
}
/* 判断是否为空 */
bool IsEmpty( MaxHeap H )
{
return !H->Size;
}
/* 建立容量为MaxSize的空的最大堆 */
MaxHeap Create( int MaxSize )
{
MaxHeap H = (MaxHeap)malloc(sizeof(struct HeapStruct));
H->Elements = (ElementType *)malloc((MaxSize+1) * sizeof(ElementType));
// Elements[0] 作为哨兵,堆元素从 Elements[1] 开始存放,因此Elements长度为MaxSize+1
H->Size = 0;
H->Capacity = MaxSize;
// "哨兵"大于堆中所有可能的值
H->Elements[0] = MaxData;
return H;
}
/* 将元素item 插入最大堆H,T(N)=O(logN) */
void Insert( MaxHeap H, ElementType item )
{
// 将新增结点插入到有序序列中
int i;
if ( IsFull(H) )
{
printf("最大堆已满");
return;
}
i = ++H->Size; // i指向插入后堆中的最后一个元素的位置
for ( ; H->Elements[i/2] < item; i/=2 ) // 如果待插入元素比其父结点的元素大
H->Elements[i] = H->Elements[i/2]; // 调换父结点与子结点元素的值
H->Elements[i] = item; // 将item插入相应位置,此时Elements[0]已经定义为哨兵
}
/* 从最大堆H中取出键值为最大的元素, 并删除一个结点 */
ElementType DeleteMax( MaxHeap H )
{
int Parent, Child;
ElementType MaxItem, temp;
if ( IsEmpty(H) )
{
printf("最大堆已为空");
return;
}
MaxItem = H->Elements[1]; // 取出根结点最大值
/* 用最大堆中最后一个元素移至根结点,开始向上过滤下层结点 */
temp = H->Elements[H->Size--];
for( Parent=1; Parent*2<=H->Size; Parent=Child )
{
Child = Parent * 2;
if( (Child!= H->Size) && (H->Elements[Child] < H->Elements[Child+1]) )
Child++; // Child指向左右子结点的较大者
if( temp >= H->Elements[Child] ) // temp的值与child元素的值比较
break; // temp 大于子结点中较大的元素,可以不用调整直接返回
else // 移动temp元素到下一层
H->Elements[Parent] = H->Elements[Child];
}
H->Elements[Parent] = temp;
return MaxItem;
}
最大堆的建立
建立最大堆:将已经存在的N个元素按最大堆的要求存放在一个一维数组中
- 方法1:通过插入操作,将N个元素一个个相继插入一个初始为空的堆中去,其时间代价最大为O(NlogN)。
- 方法2:在线性时间复杂度下建立最大堆,时间代价为O(N).
- 将N个元素按输入顺序存入,先满足完全二叉树的结构特性;
- 调整各结点位置,以满足最大堆的有序特性(从倒数第一个有儿子的结点开始做)
建堆时,最坏情况下需要挪动元素次数是等于树中各结点的高度和。
哈夫曼树和哈夫曼编码
什么是哈夫曼树(Huffman Tree)
举例是百分制的考试成绩换算成五分制的成绩,当考虑成绩分布概率时,需要修改查找树的结构以提高搜索效率。
0 | 1| 2 | 3 | 4 | 5
---|---|---|---|---|---|---
分数段 | 0-59 | 60-69 | 70-79 | 80-89 | 90-100 |
比例 | 0.05 | 0.15| 0.40| 0.30| 0.10|

左侧搜索树效率:0.05×1 + 0.15×2 + 0.4×3 + 0.3×4 + 0.1×4 = 3.15
右侧搜索树效率:0.05×3 + 0.15×3 + 0.4×2 + 0.3×2 + 0.1×2 = 2.2
定义
带权路径长度(WPL): 设二叉树有n个子结点,每个叶结点带有权值\(W_k\),从根节点到每个叶子结点的长度\(l_k\),则每个叶子结点的带权路径长度之和就是:\(\sum_{k=1}^nW_kl_k\)。
哈夫曼树或最优二叉树:WPL最小的二叉树
例:有5个叶子结点,它们的权值为{1,2,3,4,5},用次权值序列可以构造出不同形状的多个二叉树。
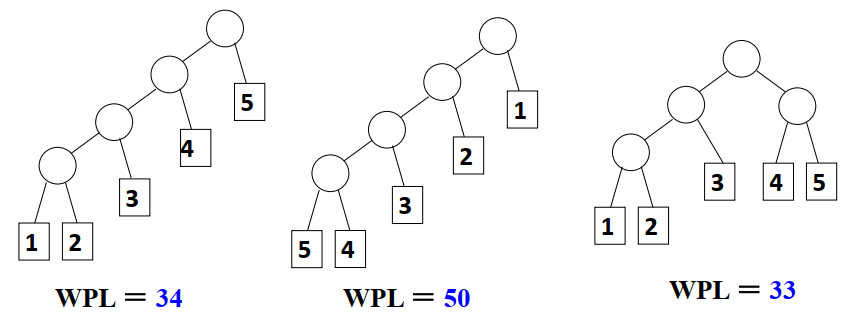
哈夫曼树的构造
每次把权值最小的两棵二叉树合并
#define MaxSize 1000
#define MinData -1000
int A[] = {1,3,5,8}; // 预先定义好一组权值
int A_length = 4; // 定义其长度
typedef struct HeapStruct *MinHeap;
typedef struct TreeNode *HuffmanTree;
struct HeapStruct
{
// 存放哈夫曼树的堆
HuffmanTree *data; // 存值的数组
int size; // 堆的当前大小
int capacity; // 最大容量
};
struct TreeNode
{
// 哈夫曼树
int Weight; //权值
HuffmanTree Left; // 左子树
HuffmanTree Right; // 右子树
}
/* 初始化哈夫曼树 */
HuffmanTree CreateHuff()
{
HuffmanTree Huff;
Huff = (HuffmanTree)malloc(sizeof(struct TreeNode));
Huff->weight = 0;
Huff->Left = NULL;
Huff->right = NULL;
return Huff;
}
/* 初始化堆 */
MinHeap CreateHeap()
{
MinHeap H;
HuffmanTree Huff;
H = (MinHeap)malloc(sizeof(struct HeapStruct));
H->data = (HuffmanTree *)malloc(sizeof(struct TreeNode) * (MaxSize+1));
H->capacity = MaxSize;
H->size = 0;
// 给堆置哨兵
Huff = CreateHuff();
Huff->weight = MinData;
H->data[0] = Huff;
return H;
}
/* 向堆H中插入元素i */
void HeapInsert( MinHeap H, int i )
{
int parent,child;
int tmp = H->data[i]->weight; // 取出当前"根结点"值
for(parent=i;parent*2<=H->size;parent = child)
{
child = 2 * parent;
if((child!=H->size) && (H->data[child+1]->weight < H->data[child]->weight))
child++;
if(H->data[child]->weight >= tmp)
break;
else
H->data[parent] = H->data[child];
}
H->data[parent]->weight = tmp;
}
/* 调整最小堆 */
void Adjust( MinHeap H )
{
for(int i =H->size/2;i>0;i--)
HeapInsert(H,i); // 每个"子最小堆"调整
}
/* 建堆 */
void BuildMinHeap( MinHeap H )
{
// 将权值读入堆中
HuffmanTree Huff;
for(int i=0;i<A_length;i++)
{
Huff = CreateHuff();
Huff->weight = A[i];
H->data[++H->size] = Huff;
}
// 调整堆
Adjust(H);
}
/* 删除最小堆元素 */
HuffmanTree Delete( MinHeap H )
{
int parent,child;
HuffmanTree T = H->data[1]; // 取出根结点的哈夫曼树
HuffmanTree tmp = H->data[H->size--]; // 取出最后一个结点哈夫曼树的权值
for(parent=1;parent*2<=H->size;parent = child)
{
child = 2 * parent;
if((child!=H->size) && (H->data[child+1]->weight < H->data[child]->weight))
child++;
if(H->data[child]->weight >= tmp->weight)
break;
else
H->data[parent] = H->data[child];
}
H->data[parent] = tmp;
// 构造一个 HuffmanTree 结点,附上刚才取出来的权值,返回该结点
return T;
}
/* 插入一个哈夫曼树 */
void HuffInsert( MinHeap H, HuffmanTree Huff )
{
int weight = Huff->weight; // 取出权值
int i = ++H->size;
for(;H->data[i/2]->weight > weight;i/=2)
H->data[i] = H->data[i/2];
H->data[i] = Huff;
}
/* 哈夫曼树的构造 */
HuffmanTree Huffman( MinHeap H )
{
/* 假设H->Size个权值已经存在H->Elements[]->Weight里 */
int i;
HuffmanTree T;
BuildMinHeap(H); // 将H->Elements[]按权值调整为最小堆
for (i = 1; i < H->Size; i++) // 做H->Size-1次合并
{
T = (HuffmanTree)malloc(sizeof(struct TreeNode)); // 建立新结点
T->Left = DeleteMin(H); // 从最小堆中删除一个结点, 作为新T的左子结点
T->Right = DeleteMin(H); // 从最小堆中删除一个结点, 作为新T的右子结点
T->Weight = T->Left->Weight+T->Right->Weight; // 计算新权值
HuffInsert(H, T); // 将新T插入最小堆
}
}
哈夫曼树的特点
- 没有度为1的结点;
- n个叶子结点的哈夫曼树共有2n-1个结点;
- 哈夫曼树的任意非叶结点的左右子树交换后仍是哈夫曼树;
- 对同意权值{\(W_1,W_2,...,W_n\)},存在不同构的两棵哈夫曼树。
哈夫曼编码
给定一段字符串,如何对字符进行编码,可以使得该字符串的编码存储空间最少?
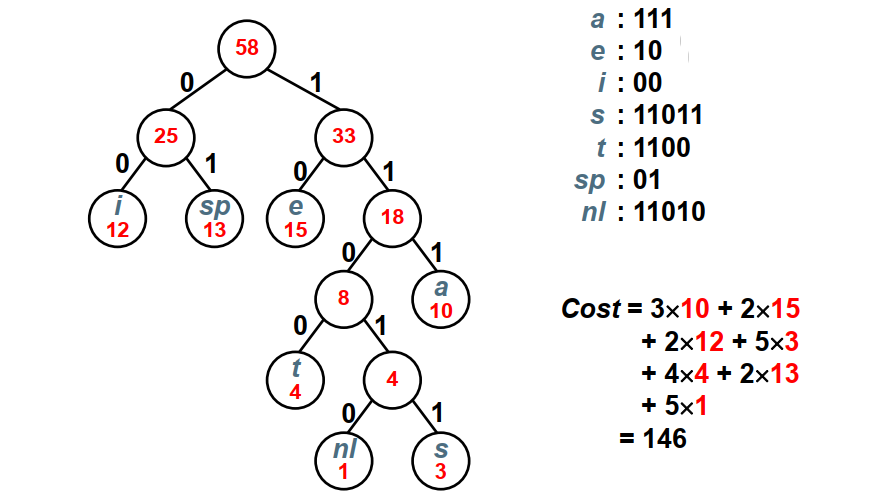
【例】 假设有一段文本,包含58个字符,并由以下7个字符构: a, e, i,s, t,空格(sp),换行(nl);这7个字符出现的次数不同。如何对这7个字符进行编码,使得总编码空间最少?
| \(C_i\) | a | e | i | s | t | sp | nl |
|:--😐:--😐:--😐:--😐:--😐:--😐 :--😐:--😐:--😐
\(f_i\) | 10 | 15 | 12 | 3 | 4 | 13 | 1 |
按照哈夫曼编码如下:
集合和运算
集合的表示
集合运算:交、并、补、差,判定一个元素是否属于某一个集合
并查集:集合并、查某元素属于什么集合
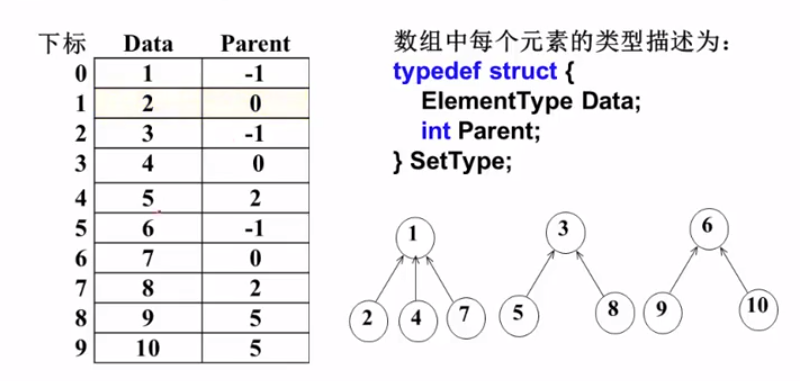
并查集中集合的存储实现:
- 用树结构表示集合,树的每个结点代表一个集合元素(双亲表示法:孩子指向双亲)
- 采用数组存储形式(负数表示根结点,非负数表示双亲结点的下标)
集合运算
(1)查找某个元素所在的集合
/* 在数组S中查找值为X的元素所属的集合*/
int Find( SetTpye S[], ElementType X )
{
/* Maxsize是全局变量,为数组S的最大长度 */
int i;
for (i=0; i<MaxSize && S[i].Data != X; i++);
if ( i>=MaxSize )
return -1; // 未找到X,返回-1
for ( ; S[i].Parent >= 0; i=S[i].Parent ); // 由Parent下标向上回溯找到根结点
return i; // 找到X所属集合,返回树根结点在数组S中的下标
}
(2)集合的并运算
- 分别找到X1和X2两个元素所在集合树的根结点(根结点可存储集合中元素的个数)
- 如果他们不同根,则将其中一个根结点的父结点指针设置成另一个根结点的数组的下标(为了改善合并后的查找性能,可以将小的集合合并到相对大的集合)
void Union( SetType S[], ElementType X1, ElementType X2 )
{
int Root1, Root2;
Root1 = Find(S, X1);
Root2 = Find(S, X2);
if (Root1 > Root2)
S[Root2].Parent = Root1;
else if (Root2 > Root1)
S[Root1].Parent = Root2;
}
应用:堆中的路径
题意理解
将一系列给定数字插入一个初始为空的小顶堆H[],随后对任意给定的下标‘i’,打印从H[i]到根结点的路径。
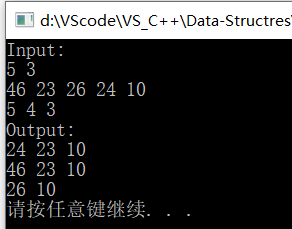
输入样例:
5 3 (代表一共有5个结点,随后有3个结点路径需要打印)
46 23 26 24 10(小顶堆的5个结点)
5 4 3 (需要打印路径的结点下标)
构成的小顶堆如下所示:
[1] 10
/ \
[2] 23 40 [3]
/ \
[4] 9 3 [5]
输出样例:
24 23 10
46 23 10
26 10
程序框架
int main()
{
1、读入n和m
2、根据输入序列键堆
3、对m个要求,打印到根的路径
return 0;
}
程序实现
#include <stdio.h>
#include <stdlib.h> //调用malloc()和free()
#include <windows.h> //windows.h里定义了关于创建窗口,消息循环等函数S
#define MAXN 1001
#define MINH -10001
int H[MAXN], size;
/* 堆初始化 */
void Create()
{
size = 0;
H[0] = MINH; // 设置岗哨
}
/* 将X插入H中 */
void Insert(int X)
{
// 这里省略检查堆是否已满的代码
int i;
for (i = ++size; H[i / 2] > X; i /= 2)
H[i] = H[i / 2];
H[i] = X;
}
/**********************************/
/* 主函数 */
/*********************************/
int main()
{
int n, m, x, i, j;
printf("Input:\n");
scanf("%d %d", &n, &m);
Create(); // 堆初始化
for (i = 0; i < n; i++) // 以逐个插入方式建堆
{
scanf("%d", &x);
Insert(x);
}
for (i = 0; i < m; i++)
{
scanf("%d", &j);
//如果用空格分开,程序就会等按下回车告诉系统用户已输入完成,程序才会判断。
if (i == 0)
printf("Output:\n");
printf("%d", H[j]);
while (j > 1) // 沿根方向输出各结点
{
j /= 2;
printf(" %d", H[j]);
}
printf("\n");
}
system("pause"); //程序暂停,显示按下任意键继续
return 0;
}
运行结果
应用:File Transfer
集合的简化表示
任何有限集合的N个元素都可以一一映射为整数0~N-1。
例:
2 6
/ \ / \
5 4 0 1
/
3
这里构造数组S,其下标为集合中结点的值,而S中元素的值则是指向集合结点的父结点的值,其中根结点的值为-1.
| 下标 | [0] | [1] | [2] | [3] | [4] | [5] | [6] |
|:--😐:--😐:--😐:--😐:--😐:--😐 :--😐:--😐:--😐
\(S\) | 6 | 6 | -1 | 4 | 2 | 2 | -1 |
typedef int ElementType; /* 默认元素可以用非负整数表示 */
typedef int SetNname; /* 默认用根结点的下标作为集合名称 */
typedef ElementType SetType[MaxSize]; /* 集合类型为一个整型数组 */
/* 查找并返回元素X所在集合的根结点 */
SetName Find( SetType S, ElementType X )
{
for ( ; S[X]>=0; X=S[X]); // 只有根结点为-1,如果元素大于0,则将X赋值为其父结点的值
return X;
}
void Union( SetType S, SetName Root1, SetName Root2 )
{
// 这里默认Root1和Root2是不同集合的根结点
S[Root2] = Root1; // 将Root1作为Root2集合的根结点
}
题意理解
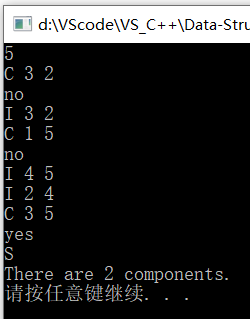
输入样例:
5 (此时有5台电脑,默认均未连接)
C 3 2 (检查电脑3,2是否连接)
I 3 2 (连接电脑3,2)
C 1 5 (检查电脑1,5是否连接)
I 4 5 (连接电脑4,5)
I 2 4 (连接电脑2,4)
C 3 5 (检查电脑3,5是否连接)
S (检查此时电脑传输有几个独立的集合)
输出样例:
no (第一次check电脑3,2)
no (第二次check电脑1,5)
yes (第二次check电脑3,5)
There are 2 components. (此时有2个独立的电脑集合)
程序框架
int main()
{
初始化集合;
do
{
读入一条指令;
处理指令;
}
while (没结束);
return 0;
}
Input_connection( s ); // 连接电脑结点--->集合的并集
Check_connection( s ); // 检查电脑结点---> 集合的查找
Check_connection( s, n ); // 检查有n个电脑结点的系统的集合---> 数集合的根
程序实现
#include <stdio.h>
#include <windows.h> //windows.h里定义了关于创建窗口,消息循环等函数S
#define MaxSize 20
typedef int ElementType; /* 默认元素可以用非负整数表示 */
typedef int SetName; /* 默认用根结点的下标作为集合名称 */
typedef ElementType SetType[MaxSize]; /* 集合类型为一个整型数组 */
void Initialization(SetType S, int n);
void Input_connection(SetType S); // 将2个编号的电脑连接,并集
void Check_connection( SetType S ); // 检查2个编号的电脑是否连接,查找集合的根结点
void Check_network( SetType S, int n ); // 检查n个结点的系统,一共有几个电脑集合,数根结点
SetName Find( SetType S, ElementType X ); // 路径压缩,找到集合根
void Union( SetType S, SetName Root1, SetName Root2 ); // 将集合按秩归并
/**********************************/
/* 主函数 */
/*********************************/
int main()
{
SetType S;
int n;
char in;
scanf("%d", &n);
Initialization(S, n);
do
{
scanf("\n%c", &in);
getchar(); // 接收每次多出来的回车
switch (in)
{
case 'I':
Input_connection(S);
break;
case 'C':
Check_connection(S);
break;
case 'S':
Check_network(S, n);
break;
}
} while (in != 'S');
system("pause"); //程序暂停,显示按下任意键继续
return 0;
}
/* 初始化 */
void Initialization(SetType S, int n)
{
for (int i = 0; i < n; i++)
S[i] = -1;
}
/* 将2个编号的电脑连接,并集 */
void Input_connection( SetType S )
{
ElementType u, v;
SetName Root1, Root2;
scanf("%d %d", &u, &v);
Root1 = Find(S, u - 1);
Root2 = Find(S, v - 1);
if (Root1 != Root2)
Union(S, Root1, Root2);
}
/* 检查2个编号的电脑是否连接,查找集合的根结点 */
void Check_connection( SetType S )
{
ElementType u, v;
SetName Root1, Root2;
scanf("%d %d", &u, &v);
Root1 = Find(S, u - 1);
Root2 = Find(S, v - 1);
if (Root1 == Root2)
printf("yes\n");
else
printf("no\n");
}
/* 检查n个结点的系统,一共有几个电脑集合,数根结点 */
void Check_network( SetType S, int n )
{
int i, counter = 0;
for (i = 0; i < n; i++)
{
if (S[i] < 0)
counter++;
}
if (counter == 1)
printf("The network is connected.\n");
else
printf("There are %d components.\n", counter);
}
/* 将集合按秩归并 */
void Union(SetType S, SetName Root1, SetName Root2)
{
// 按元素规模将小树贴到大树上
if (S[Root2] < S[Root1])
{
S[Root2] += S[Root1];
S[Root1] = Root2;
}
else
{
S[Root1] += S[Root2];
S[Root2] = Root1;
}
// 按树高将矮树贴到高树上
/*
if (S[Root2] < S[Root1])
S[Root1] = Root2;
else
{
if (S[Root1] == S[Root2])
S[Root1]--;
S[Root2] = Root1;
}
*/
}
/* 路径压缩,找到集合根的同时,让每个子结点直接指向根结点 */
SetName Find( SetType S, ElementType X)
{
if (S[X] < 0) // 找到集合的根
return X;
else
// 先找到根,把根变成X的父结点,再返回根
return S[X] = Find(S, S[X]);
}
运行结果




 浙公网安备 33010602011771号
浙公网安备 33010602011771号