题解：P13266 [GCJ 2014 Finals] Symmetric Trees

前言

哈希函数写假了调了一下午，遂写题解以记录。

思路

考虑对于一个点，怎样才是合法的。显然，当一个点的一类同构的子树有偶数个时显然可以对称，考虑奇数个时：

• 这个点是根，那么他至多可以有两类同构的数量为奇数的子树（一上一下）。
• 这个点不是根，他至多有一类（只能沿着中间那个链）。

此时直接枚举根，然后用树哈希检查树的同构，此时时间复杂度是 \(O(n^2 \log n)\) 的。我们发现，只有树的重心才能成为这个根，然后可以直接优化到 \(O(n \log n)\)。

然后你会发现你假了，还会有以下情况：

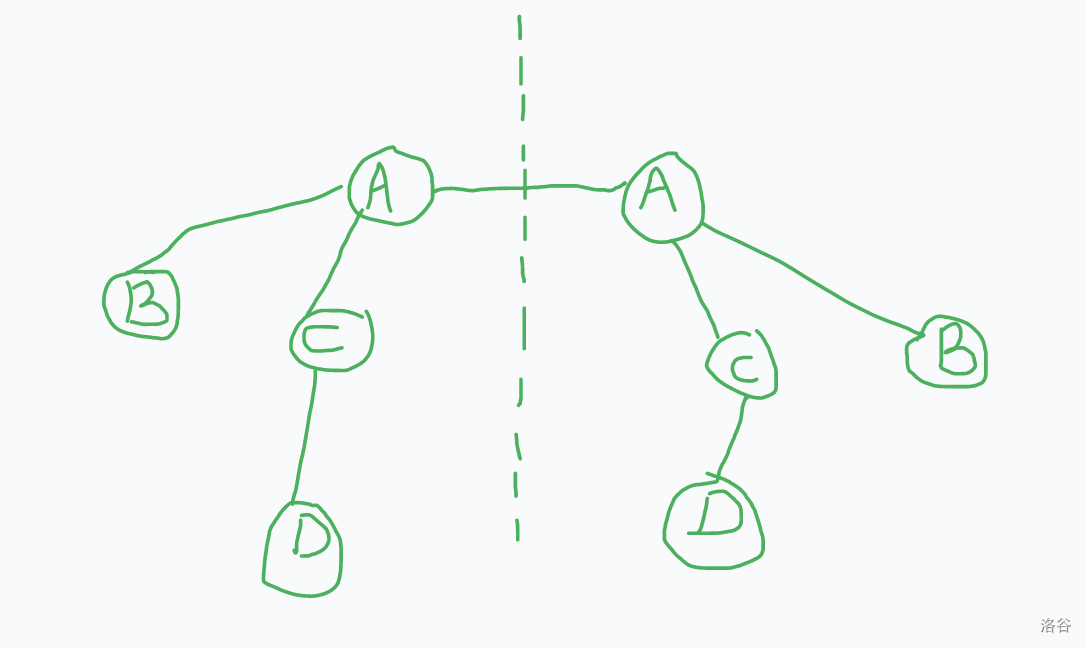
然后考虑把这条边断掉新连一个点然后以这个点为重心跑一遍即可。

代码

mt19937_64 rnd(time(NULL));
const int N = 3e6 + 20, M = 3e6 + 20,  mod = 998244353;
int T, n, col[N], val[30];
ull mask = rnd();
vector<int> G[N];
int f[N], g[N], siz[N];
int prime[M], cnt;
bool b[M];
ull F(ull x){
	x ^= mask; x ^= x << 13; x ^= x >> 7; x ^= x << 17; x ^= mask;
	return x;
}
int ms[N], root[5], tot, _siz[N];
inline void GetRoot(int u, int fa){
    ms[u] = 0; _siz[u] = 1;
    for(auto v : G[u]){
        if(v == fa) continue;
        GetRoot(v, u);
        _siz[u] += _siz[v];
        ms[u] = max(ms[u], _siz[v]);
    }
    ms[u] = max(ms[u], n - _siz[u]);
    if(ms[u] <= n / 2) root[tot++] = u;
}
map<int, pii> mp;
int ck[N];
inline bool check(int u, int fa, int tp){
    mp.clear();
    for(auto v : G[u]) if(v != fa) mp[f[v]].first++, mp[f[v]].second = v;
    int sum = 0;
    for(auto [k, pr] : mp){
        if(pr.first % 2 == 0) continue;
        else if(ck[pr.second] && (++sum) <= ((u == root[tp]) ? 2 : 1)) continue;
        else return false;
    }
    return true;
}
inline bool GetHash(int u, int fa, int tp){
    siz[u] = 1;
    f[u] = val[col[u]];
    ck[u] = 0; 
    ull res = 0;
    for(auto v : G[u]){
        if(v ^ fa){
            GetHash(v, u, tp);
            res += f[v];
            siz[u] += siz[v];
        }
    }
    f[u] += F(res);
    return (ck[u] = check(u, fa, tp));
}
inline void clear(){
    tot = 0; clr(root);
    for(int i = 1; i <= n + 1; ++i) G[i].clear(), ck[i] = 0;
}
inline void work(int qaq){
    cin >> n;
    for(int i = 1; i <= n; ++i){
        char c; cin >> c;
        col[i] = (c - 'A' + 1);
    }
    for(int i = 1, u, v; i < n; ++i) cin >> u >> v, G[u].pb(v), G[v].pb(u);
    GetRoot(1, 0);
    int flag = 0;
    if(root[0]) flag |= GetHash(root[0], 0, 0);
    if(root[1]) flag |= GetHash(root[1], 0, 1);
    if(root[0] && root[1]){
        G[root[0]].erase(find(G[root[0]].begin(), G[root[0]].end(), root[1]));
        G[root[1]].erase(find(G[root[1]].begin(), G[root[1]].end(), root[0]));
        G[root[0]].pb(n + 1);
        G[n + 1].pb(root[0]);    
        G[root[1]].pb(n + 1);
        G[n + 1].pb(root[1]);
        root[2] = n + 1;
        flag |= GetHash(n + 1, 0, 2);
    }
    if(flag) cout << "Case #" << qaq << ": SYMMETRIC" << '\n';
    else cout << "Case #" << qaq << ": NOT SYMMETRIC" << '\n';
    clear();
}
signed main(){
    #ifndef ONLINE_JUDGE
        freopen("data.in","r",stdin);
        freopen("data.out","w",stdout);
    #endif
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    for(int i = 1; i <= 26; ++i) val[i] = rnd() % mod;
    cin >> T; init();
    for(int qwq = 1; qwq <= T; ++qwq) work(qwq);
    return 0;   
}