【学校训练记录】十月个人训练赛1题解

A

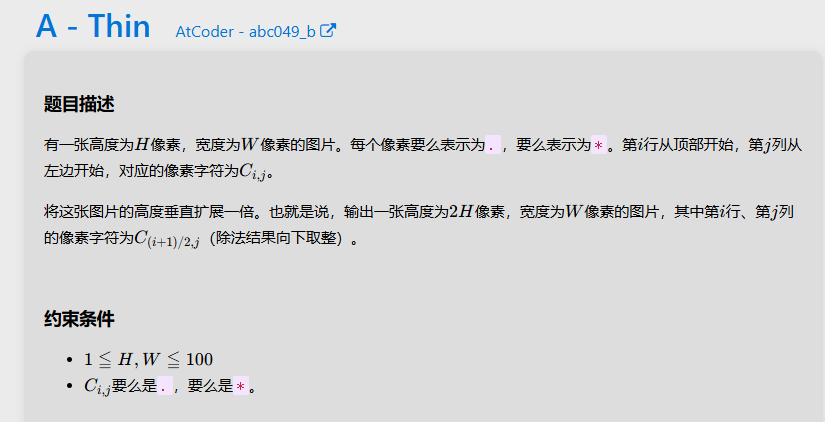
只需按照题目意思扩展h倍即可，先记录初始字符，打印时扩展为2*h根据题目公式打印

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN = 100005;
int n;
int a[MAXN];
char mp[105][105];
signed main(){
	int h, w;
	cin >> h >> w;
	for(int i = 1; i <= h; i++)
		for(int j = 1; j <= w; j++)
			cin >> mp[i][j];
	for(int i = 1; i <= 2 * h; i++){
		for(int j = 1; j <= w; j++)
			cout << mp[(i+1) / 2][j];
		cout << endl;
	}	
	return 0;
}

B

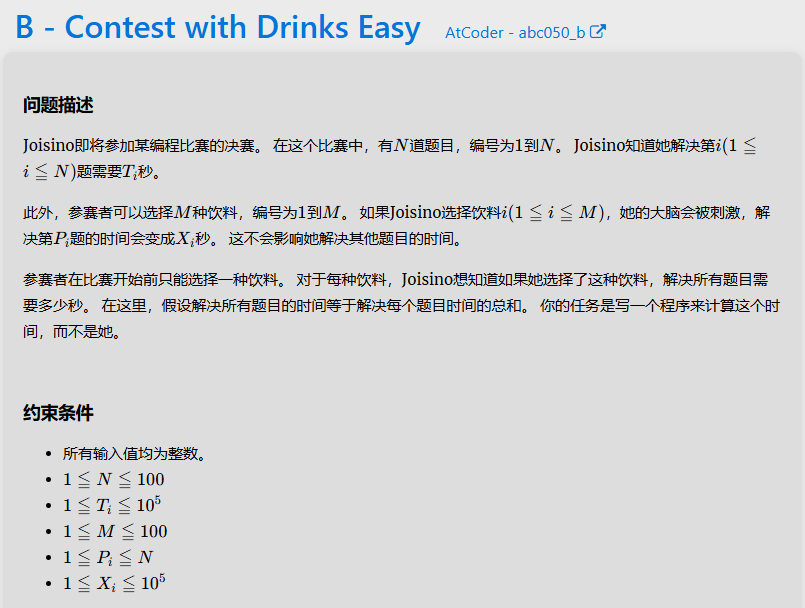
因为饮料只会改变一道题的解题时间，可以先用sum预处理记录未喝饮料的初始总时间（数据量小，不预处理直接暴力求也可），再根据每喝的一瓶饮料改变的时间进行增减即可

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN = 100005;
int n, m;
int a[MAXN];
signed main(){
	cin >> n;
	int sum = 0;
	for(int i = 1; i <= n; i++){
		cin >> a[i];
		sum += a[i];
	}
	cin >> m;
	while(m--){
		int i, t;
		cin >> i >> t;
		cout << sum - a[i] + t << endl;
	}
	return 0;
}

C

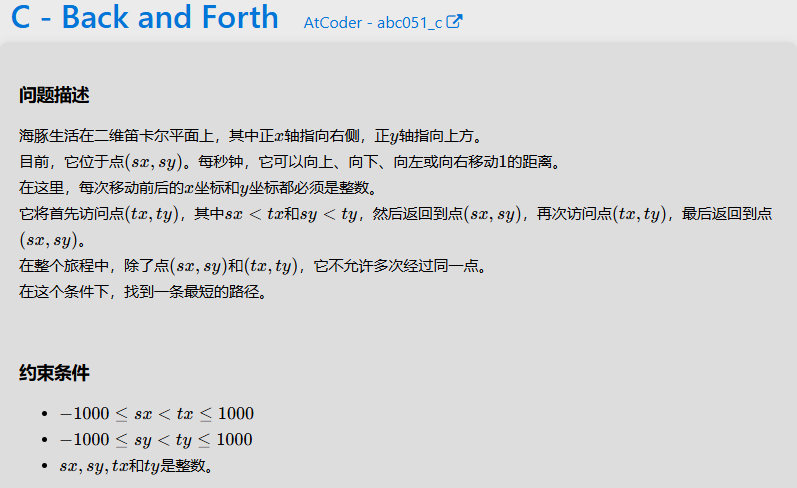
观察到目标点始终位于起始点右上角，所以就是简单的绕圈（可以画个图思考一下），纯模拟。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN = 100005;
int sx, sy, tx, ty;
signed main(){
	cin >> sx >> sy >> tx >> ty;
	int x = tx - sx;
	int y = ty - sy;
	for(int i = 1; i <= y; i++) cout << "U";
	for(int i = 1; i <= x; i++) cout << "R";
	for(int i = 1; i <= y; i++) cout << "D";
	for(int i = 1; i <= x; i++) cout << "L";
	cout << "L";
	for(int i = 1; i <= y + 1; i++) cout << "U";
	for(int i = 1; i <= x + 1; i++) cout << "R";
	cout << "D";
	cout << "R";
	for(int i = 1; i <= y + 1; i++) cout << "D";
	for(int i = 1; i <= x + 1; i++) cout << "L";
	cout << "U";
	return 0;
}

D

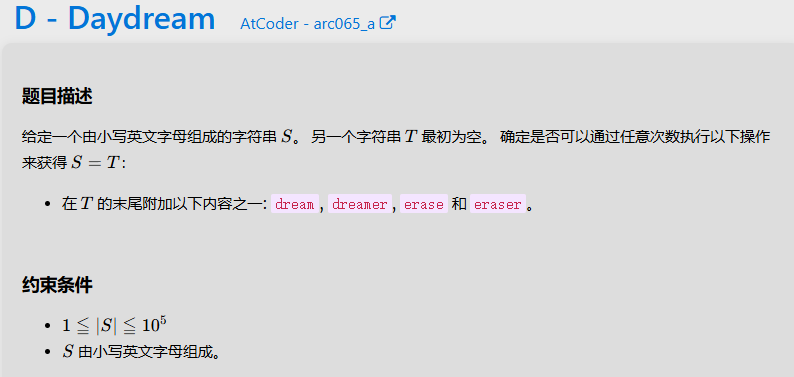
字符串模拟，考虑从左到右遍历字符串S，如果中间有不满足构成题目要求的四个单词时，即为T不能构成S。每次循环考虑一个单词，
如果不是以d或者e为头的单词必定不能构成。另外要注意一个细节，dream后的er不单是能构成dreamer，也有可能后面的字母补上凑成dreamerase，
因此需要特判dream后的er，如果能构成erase就构成，不能就构成dreamer再进行判断。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN = 100005;
signed main(){
	string s;
	string s1 = "dream", s2 = "dreamer", s3 = "erase", s4 = "eraser";
	cin >> s;
	int f = 0;  
	for(int i = 0; i < s.size(); i++){
		if(s[i] != 'd' && s[i] != 'e'){
			f = 1;
			break;
		}//如果接下来单词不是d和e开头即错误，直接break就好 
		if(s[i] == 'd'){
			for(int j = 0; j < 5; j++, i++)//判断是否是dream 
				if(s[i] != s1[j]){
					f = 1;
					break;
				}
			if(s[i] == 'e' && s[i+1] == 'r'){//特判dream后的er能否构成erase，不能的话就将er给dream 
				if(s[i+2] != 'a') i = i + 1; //不能构成，指针回溯到‘r’(即当作dreamer) 
				else i--;//能构成则指针回溯到‘m’，在下一轮循环中判断是否构成erase 
			} else i--;//在判断是否是dream时指针指向‘m’下个字符，记得回溯 
		}
		if(s[i] == 'e'){
			for(int j = 0; j < 5; j++, i++)//判断是否是erase 
				if(s[i] != s3[j]){
					f = 1;
					break;
				}
			if(s[i] != 'r') i--;//不能构成eraser，将指针回溯到‘e’ 
		}
		if(f) break;
	}
	if(f) cout << "NO" << endl;
	else cout << "YES" << endl;
	return 0; 
}

E

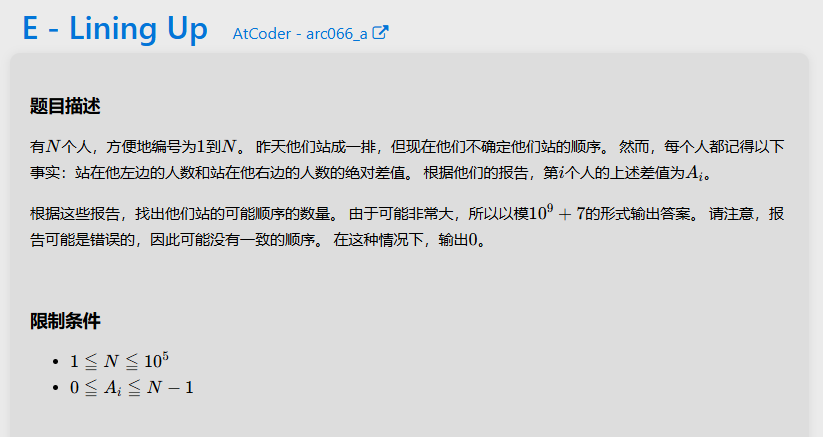
根据排队的对称性，在左右两边位置相同的人得到的数字必然是相同的，即1-n/2与n/2+1-n求出的绝对值差相同，
判断报数毛不矛盾：报数一定是俩俩相对的，并且不同数字的总数为n/2，如果n是奇数，则最中间那个人数字一定为0，并且报数的奇偶性不能与n一致（不然绝对值之差得不到这个位数）。
利用哈希表set算不同数的数量判断是否等于n/2.剩下排序总数自然就是排列组合问题了，每个位置有两种情况，只需考虑1~n/2，另一半会固定。所以是2的n/2幂次，数值较大需要用快速幂求模。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN = 100005;
const int MOD = 1e9 + 7;
unordered_set<int> st;
int qPOW(int a, int b){
	int res = 1, base = a;
	while(b){
		if(b & 1)
			res = (res * base) % MOD;
		b >>= 1;
		base = base * base % MOD;
	}
	return res;
}
signed main(){
	int n;
	cin >> n;
	int f = 0;
	for(int i = 1; i <= n; i++){
		int x;
		cin >> x;
		if(n % 2 == x % 2) f = 1;
		if(n % 2 == 1 && x == 0 && st.count(0) == 1) f = 1; //奇数排队中不可能有两个0
		st.insert(x);
	}
	if(n % 2 == 1 && st.count(0) == 0) f = 1; //奇数排队中如果没0则矛盾
	if(f || st.size() != (n + 1) / 2){
		cout << "0" << endl;
		return 0;
	}
	if(n % 2) cout << qPOW(2, st.size() - 1) << endl;
	else cout << qPOW(2, st.size()) << endl;
	return 0; 
}

F

开两个并查集记录哪些城市是道路连通，哪些城市是铁路连通。如果两个城市的道路父节点与铁路父节点一致，那么城市数量就+1，
并且这两个城市的答案一致（因为第三个城市能到达第二个城市也就能到达第一个城市），利用map的特性记录这两个父节点相通的个数即为最后的答案。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN = 200005;
const int MOD = 1e9 + 7;
int n, k, l, a, b;
map<pair<int, int>, int> mp;
int f1[MAXN], f2[MAXN];
int find(int x, int *fa){
	if(fa[x] == x) return x;
	return fa[x] = find(fa[x], fa);
}
void Union(int a, int b, int *fa){
	a = find(a, fa);
	b = find(b, fa);
	if(a != b) fa[a] = b;
}
signed main(){
	cin >> n >> k >> l;
	for(int i = 1; i <= n; i++){
		f1[i] = i;
		f2[i] = i;
	}
	for(int i = 1; i <= k; i++){
		cin >> a >> b;
		Union(a, b, f1);
	}
	for(int i = 1; i <= l; i++){
		cin >> a >> b;
		Union(a, b, f2);
	}
	for(int i = 1; i <= n; i++){
		mp[make_pair(find(i, f1), find(i, f2))]++;
	}
	for(int i = 1; i <= n; i++){
		cout << mp[make_pair(find(i, f1), find(i, f2))];
		if(i != n) cout << " ";
	}
	return 0;
}