2025 ZJ 中考数学压轴题的一种解析几何做法

特别鸣谢：Desmos 提供强大的验算支持

提示：文章含有较多 \(\LaTeX\)，可能加载时间较长，125% 缩放页面，更好的公式体验。

同步发表于 洛谷

【题目描述】

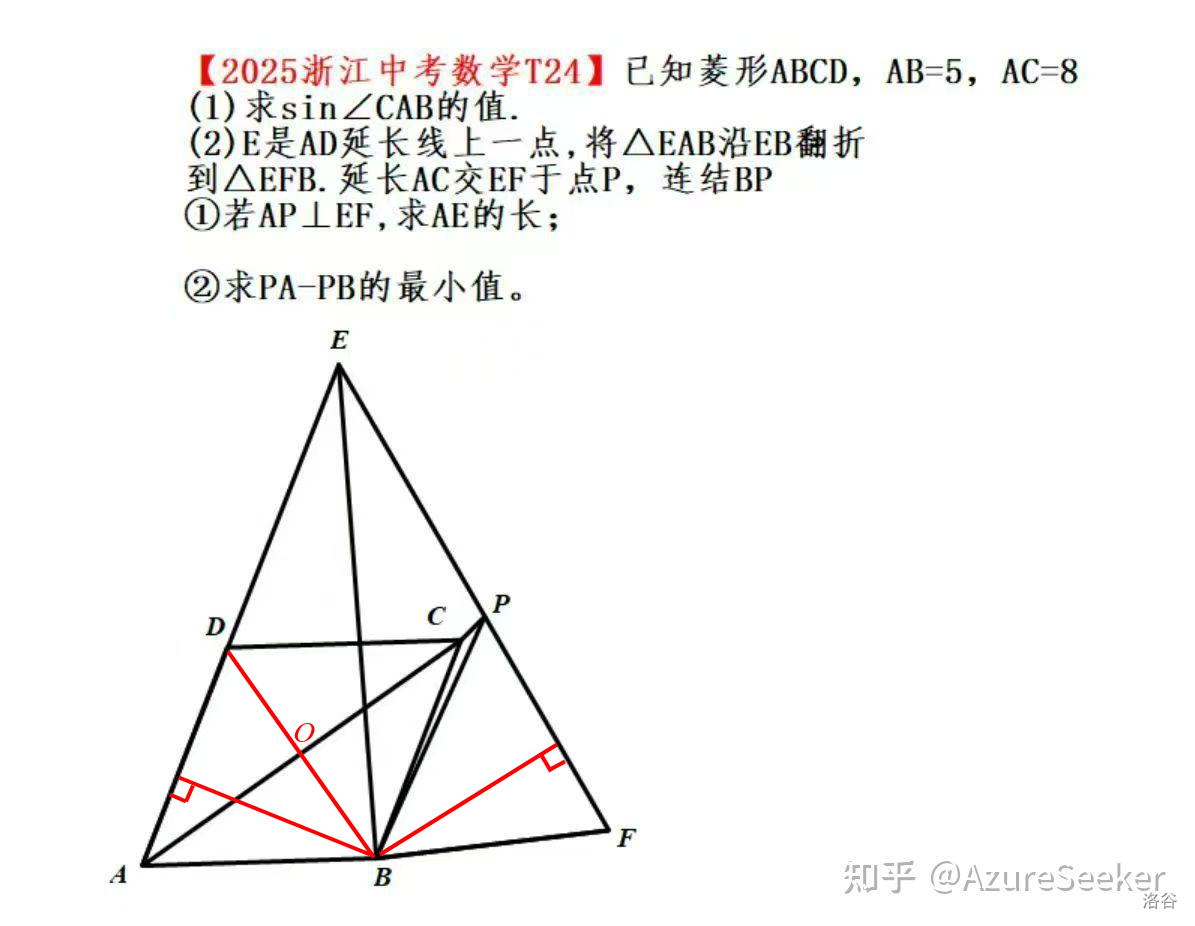
（知乎的，侵删，红色的是我加的线，帮助 STD 的讲解）

这里我们只考虑第三问即 (2).②，求 PA-PB 最小值

【一种 STD】

设 \(PO=x\)，根据 \(AB=5,AC=8\) 易得 \(OB=3\)，那么 \(PA=x+4,PB=\sqrt{x^2+9}\)

\(PA-PB=4+x-\sqrt{x^2+9}=4+\frac{\left(x-\sqrt{x^2+9}\right)\left(x+\sqrt{x^2+9}\right)}{x+\sqrt{x^2+9}}=4-\frac{9}{x+\sqrt{x^2+9}}\)

分子有理化发现 \(PA-PB\) 随着 \(x\) 减小而减小，我们只需要求 \(PO\) 最小值。

不难看出 \(BP\) 越小 \(PO\) 越小，发现 \(BP\le\left(B 到 EF 的距离\right)=\left(B 到 EA 的距离\right)=\frac{24}{5}\)，然后证明一下可以取到。

那么 \(x_{min}=\sqrt{\left(\frac{24}{5}\right)^2-3^2}=\frac{3\sqrt{39}}{5}\)

\(PA-PB=4+\frac{3\sqrt{39}}{5}-\frac{24}{5}=\frac{3\sqrt{39}-4}{5}\)

【本人无脑解析几何法】

由于本人是卑微的初二学牲，数学思维不足，因此使用解析几何法解决。

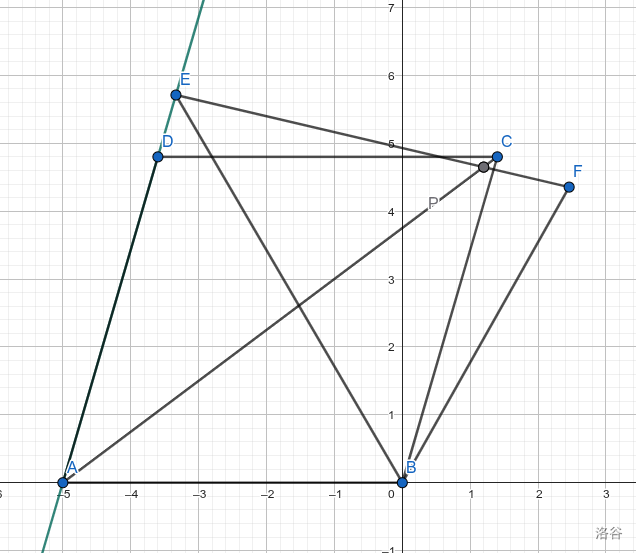
建系

以 \(B\) 为原点，\(BA\) 为 \(x\) 轴负方向建平面直角坐标系。

由题中信息可得 \(A\left(-5,0\right),C\left(\frac{7}{5},\frac{24}{5}\right),D\left(-\frac{18}{5},\frac{24}{5}\right)\)

设 \(\angle{DAB}=\alpha,\angle{CBF}=\theta\)

求 F 点坐标

\(\because \angle{DAB}=\alpha, \angle{CBF}=\theta\)

\(\therefore \angle{ABC}=180^{\circ}-\alpha,\ \ FB \ 与\ x \ 轴夹角 = \alpha-\theta\)

\(\because BF=AB=5 \ \ \ \ \therefore F\left(5\cos\left(\alpha-\theta\right),5\sin\left(\alpha-\theta\right)\right)\)

求 P 横坐标

易得 \(AC:y=\frac{3}{4}x+\frac{15}{4}\)

\(\because \angle{F}=\alpha\)

\(\therefore EF,DC \ 夹角为 \ \theta\)

\(\therefore EF \ 斜率为 -\tan\left(\theta\right) \ 且过 \ F\left(5\cos\left(\alpha-\theta\right),5\sin\left(\alpha-\theta\right)\right)\)

\(\therefore EF:y=-\tan\left(\theta\right)x+5\tan\left(\theta\right)\cos\left(\alpha-\theta\right)+5\sin\left(\alpha-\theta\right)\)

设 \(P\) 横坐标为 \(x\)

\(\frac{3}{4}x+\frac{15}{4}=-\tan\left(\theta\right)x+5\tan\left(\theta\right)\cos\left(\alpha-\theta\right)+5\sin\left(\alpha-\theta\right)\)

\(\frac{3}{4}x+\tan\left(\theta\right)x=5\tan\left(\theta\right)\cos\left(\alpha-\theta\right)+5\sin\left(\alpha-\theta\right)-\frac{15}{4}\)

和差角公式化简

\(\sin\left(\alpha-\beta\right)=\sin\left(\alpha\right)\cos\left(\beta\right)-\cos\left(\alpha\right)\sin\left(\beta\right)\)

\(\cos\left(\alpha-\beta\right)=\cos\left(\alpha\right)\cos\left(\beta\right)+\sin\left(\alpha\right)\sin\left(\beta\right)\)

利用和差角公式可得

\(\frac{3}{4}x+\tan\left(\theta\right)x=5\tan\left(\theta\right)(\left(\cos\left(\alpha\right)\cos\left(\theta\right)+\sin\left(\alpha\right)\sin\left(\theta\right)\right))+5\left(\left(\sin\left(\alpha\right)\cos\left(\theta\right)-\cos\left(\alpha\right)\sin\left(\theta\right)\right)\right)-\frac{15}{4}\)

\(\frac{3}{4}x+\tan\left(\theta\right)x=5\tan\left(\theta\right)\cos\left(\alpha\right)\cos\left(\theta\right)+5\tan\left(\theta\right)\sin\left(\alpha\right)\sin\left(\theta\right)+5\sin\left(\alpha\right)\cos\left(\theta\right)-5\cos\left(\alpha\right)\sin\left(\theta\right)-\frac{15}{4}\)

\(\frac{3}{4}x+\tan\left(\theta\right)x=5\sin\left(\theta\right)\cos\left(\alpha\right)+5\tan\left(\theta\right)\sin\left(\alpha\right)\sin\left(\theta\right)+5\sin\left(\alpha\right)\cos\left(\theta\right)-5\cos\left(\alpha\right)\sin\left(\theta\right)-\frac{15}{4}\)

\(\frac{3}{4}x+\tan\left(\theta\right)x=5\tan\left(\theta\right)\sin\left(\alpha\right)\sin\left(\theta\right)+5\sin\left(\alpha\right)\cos\left(\theta\right)-\frac{15}{4}\)

我们容易看出原图中 \(\sin\left(\alpha\right)=\frac{24}{25}\)

\(\frac{3}{4}x+\tan\left(\theta\right)x=\frac{24}{5}\tan\left(\theta\right)\sin\left(\theta\right)+\frac{24}{5}\cos\left(\theta\right)-\frac{15}{4}\)

\(x=\frac{\frac{24}{5}\tan\left(\theta\right)\sin\left(\theta\right)+\frac{24}{5}\cos\left(\theta\right)-\frac{15}{4}}{\tan\left(\theta\right)+\frac{3}{4}}\)

\(x=\frac{\frac{24}{5}\tan\left(\theta\right)\sin\left(\theta\right)+\frac{18}{5}\sin\left(\theta\right)-\frac{18}{5}\sin\left(\theta\right)+\frac{24}{5}\cos\left(\theta\right)-\frac{15}{4}}{\tan\left(\theta\right)+\frac{3}{4}}\)

\(x=\frac{24}{5}\sin\left(\theta\right)+\frac{\frac{24}{5}\cos\left(\theta\right)-\frac{18}{5}\sin\left(\theta\right)-\frac{15}{4}}{\tan\left(\theta\right)+\frac{3}{4}}\)

\(x=\frac{24}{5}\sin\left(\theta\right)+\frac{\frac{24}{5}\cos\left(\theta\right)-\frac{18}{5}\tan\left(\theta\right)\cos\left(\theta\right)-\frac{15}{4}}{\tan\left(\theta\right)+\frac{3}{4}}\)

\(x=\frac{24}{5}\sin\left(\theta\right)+\frac{\frac{24}{5}\cos\left(\theta\right)-\frac{18}{5}\tan\left(\theta\right)\cos\left(\theta\right)-\frac{27}{10}\cos\left(\theta\right)+\frac{27}{10}\cos\left(\theta\right)-\frac{15}{4}}{\tan\left(\theta\right)+\frac{3}{4}}\)

\(x=\frac{24}{5}\sin\left(\theta\right)-\frac{18}{5}\cos\left(\theta\right)+\frac{\frac{24}{5}\cos\left(\theta\right)+\frac{27}{10}\cos\left(\theta\right)-\frac{15}{4}}{\tan\left(\theta\right)+\frac{3}{4}}\)

\(x=\frac{24}{5}\sin\left(\theta\right)-\frac{18}{5}\cos\left(\theta\right)+\frac{\frac{15}{2}\cos\left(\theta\right)-\frac{15}{4}}{\tan\left(\theta\right)+\frac{3}{4}}\)

\(x=\frac{24}{5}\sin\left(\theta\right)-\frac{18}{5}\cos\left(\theta\right)+\frac{30\cos\left(\theta\right)-15}{4\tan\left(\theta\right)+3}\)

正切半角公式（万能公式）化简

设 \(k=\tan\left(\frac{\alpha}{2}\right)\)

\(\sin\left(\alpha\right)=\frac{2k}{1+k^2}\)

\(\cos\left(\alpha\right)=\frac{1-k^2}{1+k^2}\)

\(\tan\left(\alpha\right)=\frac{2k}{1-k^2}\)

设 \(k=\tan\left(\frac{\theta}{2}\right)\)

利用正切半角公式公式可得

\(x=\frac{24}{5}\times\frac{2k}{1+k^2}-\frac{18}{5}\times\frac{1-k^2}{1+k^2}+\frac{30\times\frac{1-k^2}{1+k^2}-15}{4\times\frac{2k}{1-k^2}+3}\)

\(x=\frac{48}{5}\times\frac{k}{1+k^2}-\frac{18}{5}\times\frac{1-k^2}{1+k^2}+\frac{30\times\frac{1-k^2}{1+k^2}-15}{8\times\frac{k}{1-k^2}+3}\)

\(x=\frac{48}{5}\times\frac{k}{1+k^2}-\frac{18}{5}\times\frac{1-k^2}{1+k^2}+\frac{30\times\frac{(1-k^2)^2}{1+k^2}-15(1-k^2)}{8k+3(1-k^2)}\)

\(x=\frac{48}{5}\times\frac{k}{1+k^2}-\frac{18}{5}\times\frac{1-k^2}{1+k^2}+\frac{30\times\frac{k^4-2k^2+1}{1+k^2}+15k^2-15}{-3k^2+8k+3}\)

\(x=\frac{48}{5}\times\frac{k}{1+k^2}-\frac{18}{5}\times\frac{1-k^2}{1+k^2}+\frac{30\times\frac{k^4+3}{1+k^2}-60+15k^2-15}{-3k^2+8k+3}\)

\(x=\frac{48}{5}\times\frac{k}{1+k^2}-\frac{18}{5}\times\frac{1-k^2}{1+k^2}+\frac{30\times\frac{4}{1+k^2}+30(k^2-1)-60+15k^2-15}{-3k^2+8k+3}\)

\(x=\frac{48}{5}\times\frac{k}{1+k^2}-\frac{18}{5}\times\frac{1-k^2}{1+k^2}+\frac{\frac{120}{1+k^2}+45k^2-105}{-3k^2+8k+3}\)

\(x=\frac{48}{5}\times\frac{k}{1+k^2}-\frac{18}{5}\times\frac{1-k^2}{1+k^2}+\frac{120+45k^2(1+k^2)-105(1+k^2)}{(-3k^2+8k+3)(1+k^2)}\)

\(x=\frac{48}{5}\times\frac{k}{1+k^2}-\frac{18}{5}\times\frac{1-k^2}{1+k^2}-\frac{45k^4-60k^2+15}{\left(3k+1\right)\left(k-3\right)\left(k^2+1\right)}\)

\(x=\frac{48k}{5(k^2+1)}+\frac{18k^2-18}{5(k^2+1)}-\frac{225k^4-300k^2+75}{5\left(3k+1\right)\left(k-3\right)\left(k^2+1\right)}\)

\(x=\frac{48k\left(3k+1\right)\left(k-3\right)}{5\left(3k+1\right)\left(k-3\right)\left(k^2+1\right)}+\frac{(18k^2-18)\left(3k+1\right)\left(k-3\right)}{5\left(3k+1\right)\left(k-3\right)\left(k^2+1\right)}-\frac{225k^4-300k^2+75}{5\left(3k+1\right)\left(k-3\right)\left(k^2+1\right)}\)

\(x=\frac{48k\left(3k+1\right)\left(k-3\right)+(18k^2-18)\left(3k+1\right)\left(k-3\right)-225k^4+300k^2-75}{5\left(3k+1\right)\left(k-3\right)\left(k^2+1\right)}\)

\(x=\frac{-171k^4-192k^2-21}{5\left(3k+1\right)\left(k-3\right)\left(k^2+1\right)}\)

\(x=\frac{-3\left(57k^2+7\right)\left(k^2+1\right)}{5\left(3k+1\right)\left(k-3\right)\left(k^2+1\right)}\)

\(x=\frac{-3\left(57k^2+7\right)}{5\left(3k+1\right)\left(k-3\right)}\)

\(x=-\frac{171k^2+21}{15k^2-40k-15}\)

求导得出 x 最小值

对于函数 \(f(x)=\frac{u(x)}{v(x)}\)

\(f'(x)=\frac{u'(x)v(x)-u(x)v'(x)}{\left[v(x)\right]^2}\)

\(f(k)=-\frac{171k^2+21}{15k^2-40k-15}\)

\(u(k)=-171k^2-21\)

\(u'(k)=-342k\)

\(v(k)=15k^2-40k-15\)

\(v'(k)=30k-40\)

\(f'(k)=\frac{(-342k)*(15k^2-40k-15)-(-171k^2-21)*(30k-40)}{(15k^2-40k-15)^2}=\frac{6840k^2+5760k-840}{(15k^2-40k-15)^2}\)

我们知道 \(x\) 取到最小值时，\(f'(k)=0\)

\(\therefore 6840k^2+5760k-840=0\)

\(\therefore 57k^2+48k-7=0\)

\(\therefore k_1=\frac{5\sqrt{39}-24}{57},k_2=-\frac{24+5\sqrt{39}}{57}（负数舍去）\)

\(\therefore k=\frac{5\sqrt{39}-24}{57}\)

我们回带 \(k\)：

\(f(k)=-\frac{171k^2+21}{15k^2-40k-15}\)

\(f(k)=-\frac{171\left(\frac{5\sqrt{39}-24}{57}\right)^2+21}{15\left(\frac{5\sqrt{39}-24}{57}\right)^2-40\left(\frac{5\sqrt{39}-24}{57}\right)-15}\)

\(f(k)=-\frac{\frac{1950-240\sqrt{39}}{19}}{\frac{9750-5000\sqrt{39}}{1083}}\)

\(f(k)=\frac{\left(1950-240\sqrt{39}\right)\cdot \:1083}{19\left(9750-5000\sqrt{39}\right)}\)

\(f(k)=\frac{422370000\sqrt{39}-1583887500}{879937500}\)

\(f(k)=\frac{12\sqrt{39}-45}{25}\)

求出 P 的最小坐标

\(\because P\ 在\ AC:y=\frac{3}{4}x+\frac{15}{4}\ 上\)

\(\therefore P\left(\frac{12\sqrt{39}-45}{25},\frac{3}{4}\times\frac{12\sqrt{39}-45}{25}+\frac{15}{4}\right)\)

\(\therefore P\left(\frac{12\sqrt{39}-45}{25},\frac{9\sqrt{39}+60}{25}\right)\)

求出 PA-PB

\(\because A\left(-5,0\right),B\left(0,0\right)\)

\(\therefore PA=\sqrt{\left(5+\frac{12\sqrt{39}-45}{25}\right)^2+\left(\frac{9\sqrt{39}+60}{25}\right)^2}=\frac{3\sqrt{39}+20}{5}\)

\(\therefore PB=\sqrt{\left(\frac{12\sqrt{39}-45}{25}\right)^2+\left(\frac{9\sqrt{39}+60}{25}\right)^2}=\frac{24}{5}\)

\(\therefore PA-PB=\frac{3\sqrt{39}+20}{5}-\frac{24}{5}\)

\(\therefore PA-PB=\frac{3\sqrt{39}-4}{5}\)

【一些后记】

只会用解析几何，菜完了 /kel 。

同时申明本人并不会和差角公式、正切半角公式和带分数的函数化简，都是现学的。

在此拜谢场\(\tiny{几乎}\)切了这个题的 lzq。