金融数据分析(二)
金融时间序列线性模型
本部分内容是关于金融数据分析的学习内容第二部分
相关性和*稳性
*稳性
衡量两个或多个变量(或同一个变量在不同时间点)之间线性关联程度的统计量。
-
*稳性:一个时间序列的统计特性(主要是均值和方差,更严格地包括协方差结构)不随时间推移而改变。这是大多数经典时间序列模型(AR, MA, ARMA, ARIMA)的基本要求。
时间轴上面,一个点是一天的价格,k天的价格便是一个线段,这个线段在时间轴上滑动是,对应的价格的联合分布不变,这就是严*稳。
\(r_{t_ {i}}\) 代表 \(t_ {i}\) 时刻下的价格这个随机变量, t是你滑动的距离
F( \(r_ {t_ {1}}\) , \(r_ {t_ {2}}\) , \(\cdots\) , \(r_ {t_ {k}}\))=F(\(r_ {t_ {1}+t}\), \(r_ {t_ {2}+t}\), \(\cdots\) , \(r_ {t_ {k}+t}\))
弱*稳是\(r_{t}\)的均值、\(r_{t}和r_{t-l}\)的协方差不随时间的变化而变化,从直观上理解,我们要求一段段时间价格的分布是不变的
(1)E(\(r_ {t}\) )= \(\mu\)
(2)Cov( \(r_ {t}\) , \(t_ {t-l}\) )
\(\gamma\) ,l是间隔距离
原始价格序列(如股价)通常是非*稳的! 它们常常表现出:长期上涨或下跌。随时间有小幅的、方向性的移动。波动性会随时间变化(如波动聚集现象 - 高波动期后往往跟着高波动期)。
常见*稳性处理:差分 (Differencing):这是最常用、最有效的方法。计算相邻观测值之间的变化量:\(ΔY_t = Y_t - Y_{t-1}\)。一次差分通常能消除线性趋势。金融中常用收益率(价格的对数差分:\(r_t = log(P_t) - log(P_{t-1}) ≈ (P_t - P_{t-1}) / P_{t-1}\))作为分析对象,它通常比原始价格更接**稳(尽管可能仍有波动聚集)。
相关性
时间间隔为l的自相关系数为
\(\rho_{l}\)= \(\frac {Cov(r_ {t},r_ {t-l)}}{\sqrt {Var(r_ {t})Var(r_ {t-\iota})}}\) = \(\frac {Cov(r_ {t},r_ {t-l})}{Var(r_ {t})}\) = \(\frac {\gamma _ {l}}{\gamma _ {0}}\)
\(\widehat\rho_{g}\)= \(\frac {\sum _ {t=l+1}^{T}(r_ {t}-\overline{r})(r_ {t-l}-\overline {r})}{\sum _ {t=1}^ {T}(r_ {t}-r)^ {2}}\) ,
0 \(\leqslant\) l<T-1
自相关性 (Autocorrelation): 这是时间序列分析特有的、最核心的相关性概念。它衡量同一个时间序列中,当前值与其过去值(称为“滞后值”)之间的线性关系。
简单自回归模型(AR模型)
如果 \(\rho_{1} \neq 0\),则 \(X_{t}\) 与 \(X_{t-1}\) 相关,可以用 \(X_{t-1}\) 预测 \(X_{t}\)。最简单的预测为线性组合,如下模型:
称为一阶自回归模型(Autoregression model),记作 AR(1)模型。其中 \(\{\varepsilon_{t}\}\) 是零均值独立同分布白噪声序列,方差为 \(\sigma^{2}\),并设 \(\varepsilon_{t}\) 与 \(X_{t-1}\), \(X_{t-2}\), …独立。系数 \(|\phi_{1}| < 1\)。更一般的定义中仅要求 \(\{\varepsilon_{t}\}\) 是零均值白噪声,不要求独立同分布。
与一元线性回归模型的区别
这个模型与一元线性回归模型 \(Y_{i} = \phi_{0} + \phi_{1} x_{i} + \varepsilon_{i}\) 在某些方面类似(\(\varepsilon_{t}\) 是误差项)。但自回归模型中自变量 \(X_{t-1}\) 在 \(t-1\) 时刻是因变量,因此 因变量和自变量是同一变量的不同时刻。回归模型的理论结果不能直接应用于自回归模型。
AR(1)模型的性质
-
马尔可夫性(Markov性):
\(X_{t}\) 在 \(X_{t-1}, X_{t-2}, …\) 条件下的条件分布只与 \(X_{t-1}\) 有关。已知 \(X_{t-1}\) 后,用 \(\{X_{t-1}, X_{t-2}, …\}\) 预测 \(X_{t}\) 与仅用 \(X_{t-1}\) 预测效果相同。 -
条件期望与条件方差:
\[\begin{aligned} E\left(X_{t} \mid X_{t-1}\right) &= \phi_{0} + \phi_{1} X_{t-1}, \\ \operatorname{Var}\left(X_{t} \mid X_{t-1}\right) &= \sigma^{2} \end{aligned} \]即 \(X_{t-1} = x_{t-1}\) 已知时,\(X_t\) 的条件分布期望为 \(\phi_{0} + \phi_{1} x_{t-1}\),方差为 \(\sigma^{2}\)。
可以证明:\[\operatorname{Var}\left(X_{t}\right) = \frac{\sigma^{2}}{1-\phi_{1}^{2}} \]由于 \(|\phi_1| < 1\),条件方差 \(\sigma^{2}\) 小于无条件方差 \(\frac{\sigma^{2}}{1-\phi_{1}^{2}}\)。这表明 用 \(X_{t-1}\) 预测能减小 \(X_t\) 的波动。
AR(p)模型(推广形式)
AR(1) 模型可推广为 AR(p) 模型:
其中 \(\{\varepsilon_{t}\}\) 是零均值独立同分布白噪声序列,方差为 \(\sigma^{2}\),且 \(\varepsilon_{t}\) 与 \(X_{t-1}, X_{t-2}, …\) 独立。
系数约束条件
系数 \(\phi_{1}, \ldots, \phi_{p}\) 需满足:
方程
的所有复根 \(z_*\) 均满足 \(|z_*| > 1\)。
- 该多项式称为 AR(p) 模型的特征多项式,其根称为 特征根。
- 此条件称为 “特征根都在单位圆外”。
- *注:部分教材将特征根的倒数定义为特征根,此时条件等价为根的模小于 1。对 AR(1),此条件即要求 \(|\phi_1| < 1\)。
简单移动*均模型
简单移动*均模型(通常指 MA(q) 模型,其中 q 是阶数)的核心思想是:时间序列的当前值,可以用其过去一段时间内无法预测的“冲击”或“新息”(即误差项)的线性组合来解释和预测。 它捕捉的是序列对过去随机冲击的短期记忆。
模型定义 (MA(q)):
对于一个时间序列 \({Y_t}\),一个 q 阶的移动*均模型 MA(q) 定义为:
\(Y_t = μ + ε_t + θ_1 * ε_{t-1} + θ_2 * ε_{t-2} + ... + θ_q * ε_{t-q}\)
逐项解释:
\(Y_t\): 时间序列在时刻 t 的当前值。
μ (Mean / Constant): 序列的长期均值(期望值)。当所有冲击为零时,序列会趋向于这个均值。
\(ε_t\)(Current Shock / Innovation / Error Term): 当前时刻的随机冲击/新息/误差项。它代表了在时刻 t 发生的、完全不可预测的新信息(例如,意外的经济新闻、突发政治事件等)。
与 AR 模型一样,\(ε_t\) 必须满足白噪声假设:
均值为零 (E[\(ε_t\)] = 0)
常数方差 (Var(\(ε_t\)) = σ²)
无自相关 (Cov\((ε_t, ε_s)\) = 0 for t ≠ s)
通常假设独立同分布(i.i.d.),特别是服从正态分布(便于推断)。
\(ε_{t-1}, ε_{t-2}, ..., ε_{t-q}\): 过去 q 个时刻的随机冲击/新息/误差项。这些是发生在 t-1, t-2, ..., t-q 时刻的、当时不可预测的事件的影响。
\(θ_1, θ_2, ..., θ_q\) (Moving Average Coefficients / Parameters): 移动*均系数。这是模型的核心参数。
每个 \(θ_k\) 衡量了对应过去冲击项 \(ε_{t-k}\) 对当前值 \(Y_t\) 的持续影响强度和方向。
\(θ_1\) 表示上一个冲击 \(ε_{t-1}\) 对当前值 \(Y_t\) 的影响。
\(θ_2\) 表示上上个冲击 \(ε_{t-2}\) 的影响。
以此类推,直到 \(θ_q\) 表示 q 期之前的冲击 \(ε_{t-q}\) 的影响。
系数的符号表示影响方向(正面冲击/负面冲击的后续影响),绝对值大小表示影响的持续时间和强度。\(θ_k\) 的绝对值通常随着 k 增大而减小,表示冲击的影响会随时间衰减。
简单ARMA模型
核心思想:
ARMA 模型认为,一个时间序列的当前值 (\(Y_t\)) 同时受到以下两个因素的影响:
自身过去值的影响 (AR 部分):捕捉序列内部的持续性或惯性(例如,昨天的收益率对今天的影响)。
过去随机冲击的影响 (MA 部分):捕捉序列对过去不可预测事件(新息)的反应(例如,前天发生的意外新闻对今天收益率的残留影响)。
模型定义 (ARMA(p, q)):
对于一个时间序列 \({Y_t}\),一个阶数为 (p, q) 的 ARMA 模型定义为:
\(Y_t = c + φ_1 Y_{t-1} + φ_2 Y_{t-2} + ... + φ_p Y_{t-p} + ε_t + θ_1 ε_{t-1} + θ_2 ε_{t-2} + ... + θ_q ε_{t-q}\)
逐项解释:
\(Y_t\): 时间序列在时刻 t 的当前值。
c (Constant / Intercept): 模型的常数项。
AR(p) 部分 \((φ_1 Y_{t-1} + ... + φ_p Y_{t-p})\):
\(φ_1, φ_2, ..., φ_p\):自回归系数。
\(Y_{t-1}, Y_{t-2}, ..., Y_{t-p}\):序列自身的 p 个滞后值。
这部分与纯 AR(p) 模型含义完全相同。
\(MA(q) 部分 (θ_1 ε_{t-1} + ... + θ_q ε_{t-q}):\)
\(θ_1, θ_2, ..., θ_q\):移动*均系数。
\(ε_{t-1}, ε_{t-2}, ..., ε_{t-q}\):过去 q 个时刻的随机冲击/新息/误差项。
这部分与纯 MA(q) 模型含义完全相同。
\(ε_t (Current Shock / Innovation / Error Term)\): 当前时刻的随机冲击/新息/误差项。它是模型在时刻 t 无法解释的、完全随机的部分,满足白噪声假设
ARMA(p, q) 模型要求时间序列 {Y_t} 是弱*稳的(均值、方差、协方差恒定)。这是模型可靠的基础。
如果原始序列(如股价)不*稳,需要先进行转换(如计算对数收益率 \(r_t = ln(P_t) - ln(P_{t-1})\)),使其满足*稳性要求,然后再对*稳的收益率序列建立 ARMA 模型。
模型识别
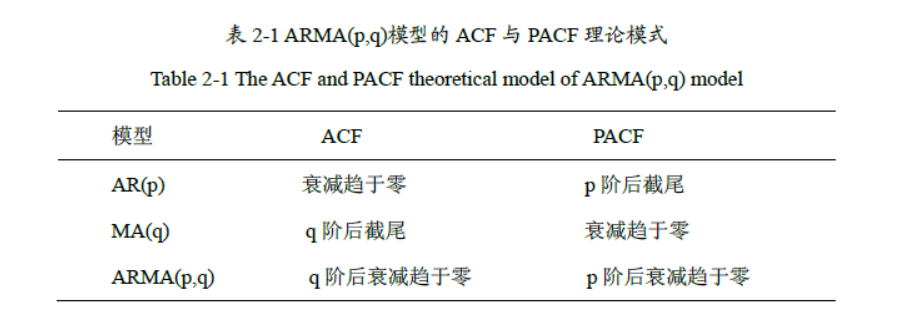
补充:
PACF:
PACF 度量 \(Y_t\) 与 \(Y_{t-k}\) 之间的直接线性相关性,即在控制中间滞后项 \(Y_{t-1}, Y_{t-2}, \dots, Y_{t-k+1}\) 的条件下的相关性。
滞后 \(k\) 的 PACF 记为 \(\phi_{kk}\),是以下回归模型的最后一个系数:
\(Y_ {t}\) = \(\phi _ {0}\) + \(\phi _ {k1}\) \(Y_ {t-1}\) + \(\phi\) \(k_ {2}\) \(Y_ {t-2}\) + \(\cdots\) + \(\phi _ {kk}\) \(Y_ {t-k}\) + \(\epsilon_{t}\)
PACF 的精确计算 (Yule-Walker 方程)
\(\phi_{kk}\) 可通过求解以下方程组获得:
其中 \(\rho_j\) 是滞后 \(j\) 的 ACF。
\(\phi_{kk}\) 是方程组的最后一个解,可用 Cramer 法则或 Durbin-Levinson 递归算法计算。
截尾 (Cut-off)
定义: 指函数(ACF 或 PACF)在某个特定的滞后阶数 k 之后,其值突然变得非常小(在统计意义上不显著),并且持续保持在零附*波动(落在置信区间内)。
拖尾 (Tails off / Decays Gradually)
定义: 指函数(ACF 或 PACF)随着滞后阶数 k 的增加,其值逐渐减小(衰减),但不会在某个特定的 k 之后突然严格为零或完全不显著。衰减方式可以是指数衰减(常见于 AR 模型)或震荡衰减(正负交替减小)。
确定阶数P和Q
主要使用AIC和BIC,选择 AIC/BIC 值最小的模型
设定一个合理的 (p, q) 搜索范围(例如 p=0 to 5, q=0 to 5)。
为范围内每一对 (p, q) 组合拟合一个 ARMA(p, q) 模型。
计算每个模型的 AIC 和 BIC 值。
选择 AIC 和 BIC 值都较小(通常是最小)的那个 (p, q) 组合。有时 AIC 和 BIC 的选择结果会不一致(BIC 对参数个数惩罚更重,倾向于选择更简单的模型),需要结合其他信息判断。
单位根非*稳时间序列
核心概念
单位根非*稳性是时间序列分析中最关键的非*稳类型,指序列包含单位根(Unit Root),其统计特性(均值、方差)随时间系统性变化。这种非*稳性无法通过简单去趋势消除,需特殊处理。
数学定义
一个时间序列 \({Y_t}\) 满足:
当特征方程 \(1 - \phi_1 z - \phi_2 z^2 - \cdots - \phi_p z^p = 0\) 存在根 \(z=1\)(即单位根)时,序列非*稳。
\(Y_ {t}\) = \(\phi _ {1}\) \(Y_ {t-1}\) + \(\phi _ {2}\) \(Y_ {t-2}\) + \(\cdots\) + \(\phi _ {p}\) \(Y_ {t-p}\) + \(\varepsilon _ {t}\)
最常见形式 - 随机游走(Random Walk):
\(Y_ {t}\) = \(Y_ {t-1}\) + \(\varepsilon _ {t}\)
其中 \(\varepsilon_t \sim iid(0,\sigma^2)\) 为白噪声
ARIMA模型
概念
ARIMA模型全称为自回归差分移动*均模型(Autoregressive Integrated Moving Average Model)。ARIMA模型主要由三部分构成,分别为自回归模型(AR)、差分过程(I)和移动*均模型(MA)。
ARIMA模型的基本思想是利用数据本身的历史信息来预测未来。一个时间点上的标签值既受过去一段时间内的标签值影响,也受过去一段时间内的偶然事件的影响,这就是说,ARIMA模型假设:标签值是围绕着时间的大趋势而波动的,其中趋势是受历史标签影响构成的,波动是受一段时间内的偶然事件影响构成的,且大趋势本身不一定是稳定的
如果不考虑差分,公式可以表示为
\(Y_ {t}\) =c+ \(\varphi _ {1}\) \(Y_ {t-1}\) + \(\varphi _ {2}\) \(Y_ {t-2}\) + \(\cdots\) + \(\varphi _ {p}\) \(Y_ {t-p}\) + \(\theta _ {1}\) \(\in _ {t-1}\)+\(\theta _ {2}\) \(\in _ {t-2}\) + \(\cdots\) + \(\theta _ {q}\) \(\in _ {t-q}\)+ \(\epsilon _ {t}\)
值得注意的是,MA模型中代表长期趋势的均值μ并不存在于ARIMA模型的公式当中,因为ARIMA模型中“预测长期趋势”这部分功能由AR模型来执行,因此AR模型替代了原本的μ 。在ARIMA模型中,c可以为0。
另外,这个公式的基础是假设我们正在处理的时间序列是*稳的,这样我们可以直接应用AR和MA模型。如果时间序列是非*稳的,那么我们就需要考虑ARIMA模型中的I部分,也就是进行差分处理。
差分过程
差分阶数
具体地说,二阶差分就是对一阶差分后的序列再次进行差分。如果我们有一个时间序列 \(Y_{t}\),那么该序列的二阶差分就可以定义为:
这样,我们得到一个新的时间序列,其每一个值都是原时间序列中相邻两个值的差的差。
因此,n阶差分就是在原始数据基础上进行n次一阶差分。在现实中,我们使用的高阶差分一般阶数不会太高。在ARIMA模型中,超参数d最常见的取值是0、1、2这些很小的数字。
滞后过程
假设我们有以下一组时间序列数据:
-
右移操作:将原序列向右移动一个单位,得到:
\[\{ \_, 4, 8, 6, 5, 3, 4 \} \]- 注:
_表示右移产生的空位
- 注:
-
删除超出数据点:移除移动后超出的数据(首位的空位和末位的冗余值),得到一阶滞后序列:
\[\{ 4, 8, 6, 5, 3 \} \] -
在⼀阶滞后序列基础上右移:将⼀阶滞后序列向右移动一个单位,得到:
\[\{ \_, \_, 4, 8, 6, 5, 3 \} \] -
删除超出数据点:移除移动后超出的数据,得到⼆阶滞后序列:
\[\{ 4, 8, 6, 5 \} \]
滞后差分
滞后差分(Lag Differences)是在进行差分操作时,不是用相邻的观测值进行相减,而是用相隔一定数量(即滞后数量)的观测值进行相减。这种操作通常在时间序列具有周期性的情况下非常有用,例如,当我们处理的数据随季节有规律地波动或者随一周的时间有规律地波动时。
给定时间序列数据:
2步滞后差分(lag-2 Differences)的计算过程如下:
-
对序列执行滞后2差分运算:
- \(6 - 5 = 1\)
- \(7 - 4 = 3\)
- \(9 - 6 = 3\)
- \(12 - 7 = 5\)
(即当前值减去与其相隔1个样本的索引较小值)
-
获得新序列:
\[X_{lag_{2}} = [1, 3, 3, 5] \] -
操作本质:
令序列中索引较大的值减去与其相隔(lag-1)个样本的索引较小值\[X_t - X_{t-k} \quad \text{(其中 } k = \text{滞后阶数)} \] -
多步差分特性:
- 带滞后的差分称为多步差分(如滞后2时为2步差分)
- 相比高阶差分应用更广泛
-
时间序列应用场景:
适用于处理周期性波动数据,例如:- 季节性波动(夏季值高 → 冬季值低)
- 周周期波动(周末值高 → 工作日值低)
参数d
滞后运算(Lag Operator)特指时间序列中“向过去移动一个时间单位”的运算,通常简写为字母 B(Backshift)或 L(Lag)。该运算可应用于单一时序样本或整个时间序列。
假设有一个时间序列 \(y_t\),定义滞后运算符 \(B\) 满足:
通过指数形式扩展为滞后 \(n\) 个时间步长:
相邻观测值之间的差可表示为:
相隔 \(n-1\) 个时间单位的差分运算:
关键结论:对数据进行 \(n\) 阶差分可直接通过滞后运算 \((1 - B^n)\) 实现
关于ARIMA模型更详细的参考,可以阅读ARIMA这篇文章
实验demo——基于ARIMA模型的中国居民消费价格指数预测
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from statsmodels.tsa.arima.model import ARIMA
from statsmodels.tsa.statespace.sarimax import SARIMAX
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.stats.diagnostic import acorr_ljungbox
from sklearn.metrics import mean_squared_error, mean_absolute_error
from scipy import stats
import warnings
warnings.filterwarnings('ignore')
class ImprovedCPIPredictor:
def __init__(self, data_file):
self.data_file = data_file
self.data = None
self.train_data = None
self.val_data = None
self.test_data = None
self.model = None
self.fitted_model = None
self.predictions = None
self.val_predictions = None
self.best_params = None
self.is_stationary = False
self.diff_order = 0
def load_data(self):
"""加载CPI数据"""
print("正在加载CPI数据...")
try:
# 读取数据
self.data = pd.read_csv(self.data_file, sep='\t', header=None,
names=['日期', 'CPI'])
#由于数据文件没有标题行 names=['日期', 'CPI']: 手动指定列名为"日期"和"CPI"
# 转换日期格式
self.data['日期'] = pd.to_datetime(self.data['日期'].str.replace('年', '-').str.replace('月份', ''))
self.data.set_index('日期', inplace=True)
self.data.sort_index(inplace=True)
# 数据清洗
self.data = self.data.dropna()
# 检查数据异常值
Q1 = self.data['CPI'].quantile(0.25)
Q3 = self.data['CPI'].quantile(0.75)
IQR = Q3 - Q1
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR
outliers = self.data[(self.data['CPI'] < lower_bound) | (self.data['CPI'] > upper_bound)]
if len(outliers) > 0:
print(f"发现{len(outliers)}个异常值")
print(outliers)
# 四分位数计算:
# Q1:将数据从小到大排列,位于25%位置的值
# Q3:将数据从小到大排列,位于75%位置的值
# IQR = Q3 - Q1,表示中间50%数据的分布范围
# 异常值边界计算:
# 下界 = Q1 - 1.5×IQR
# 上界 = Q3 + 1.5×IQR
# 这个系数1.5是统计学中的常用值,可根据需求调整(更宽松用3,更严格用1)
print(f"数据加载完成,共{len(self.data)}条记录")
print(f"时间范围:{self.data.index.min()} 到 {self.data.index.max()}")
# 基本统计信息
print("\n数据基本统计信息:")
print(self.data.describe())
return self.data
except Exception as e:
print(f"数据加载失败:{e}")
return None
def check_stationarity(self, data):
"""检查时间序列的*稳性"""
print("\n=== *稳性检验 ===")
# ADF检验
result = adfuller(data.dropna())
print(f'ADF统计量: {result[0]:.4f}')
print(f'p值: {result[1]:.4f}')
print(f'临界值:')
for key, value in result[4].items():
print(f'\t{key}: {value:.4f}')
is_stationary = result[1] <= 0.05
if is_stationary:
print("结论: 时间序列是*稳的 (p值 < 0.05)")
else:
print("结论: 时间序列不是*稳的 (p值 >= 0.05)")
# 如果不*稳,尝试差分
diff_data = data.copy()
max_diff = 2 # 最多进行2阶差分
for d in range(1, max_diff + 1):
print(f"\n尝试{d}阶差分...")
diff_data = diff_data.diff().dropna()
# 对差分后的数据进行ADF检验
diff_result = adfuller(diff_data.dropna())
print(f'差分后ADF统计量: {diff_result[0]:.4f}')
print(f'差分后p值: {diff_result[1]:.4f}')
if diff_result[1] <= 0.05:
print(f"经过{d}阶差分后,时间序列变得*稳 (p值 < 0.05)")
self.diff_order = d
is_stationary = True
break
else:
print(f"{d}阶差分后,时间序列仍不*稳 (p值 >= 0.05)")
if not is_stationary:
print("\n警告: 即使经过差分处理,时间序列仍不*稳")
print("建议: 1) 考虑季节性差分")
print(" 2) 检查是否存在结构性变化")
print(" 3) 考虑使用其他转换方法(如对数转换)")
self.is_stationary = is_stationary
return is_stationary
def split_data(self, train_size=0.6, val_size=0.2, test_size=0.2):
"""分割训练集、验证集和测试集"""
print(f"\n=== 数据分割 ===")
total_len = len(self.data)
train_end = int(total_len * train_size)
val_end = int(total_len * (train_size + val_size))
self.train_data = self.data.iloc[:train_end]
self.val_data = self.data.iloc[train_end:val_end]
self.test_data = self.data.iloc[val_end:]
print(f"训练集: {len(self.train_data)} 条记录")
print(f"验证集: {len(self.val_data)} 条记录")
print(f"测试集: {len(self.test_data)} 条记录")
return self.train_data, self.val_data, self.test_data
def find_best_arima_params(self, max_p=3, max_d=2, max_q=3):
"""寻找最佳ARIMA参数(增强版)"""
print(f"\n=== 寻找最佳ARIMA参数 ===")
best_aic = float('inf')
best_params = None
results = []
# 如果已经通过差分使数据*稳,则从已知的差分阶数开始
if self.is_stationary and self.diff_order > 0:
d_range = [self.diff_order]
print(f"使用已确定的差分阶数: d = {self.diff_order}")
else:
d_range = range(max_d + 1)
print("搜索最优差分阶数...")
for p in range(max_p + 1):
for d in d_range:
for q in range(max_q + 1):
try:
# 使用训练数据拟合模型
model = ARIMA(self.train_data['CPI'], order=(p, d, q))
fitted_model = model.fit()
# 计算AIC和BIC
aic = fitted_model.aic
bic = fitted_model.bic
# 检查模型的稳定性
if hasattr(fitted_model, 'arroots'):
ar_roots = fitted_model.arroots
if len(ar_roots) > 0 and np.any(np.abs(ar_roots) <= 1):
continue # 跳过不稳定的模型
# 检查残差的白噪声性
resid = fitted_model.resid
lb_test = acorr_ljungbox(resid, lags=[10], return_df=True)
if lb_test.iloc[0]['lb_pvalue'] < 0.05:
continue # 跳过残差不是白噪声的模型
results.append((p, d, q, aic, bic))
if aic < best_aic:
best_aic = aic
best_params = (p, d, q)
print(f"找到更好的参数: ARIMA{best_params} (AIC: {best_aic:.4f})")
except Exception as e:
continue
if not results:
print("未找到有效的ARIMA参数组合")
return None
# 显示前5个最佳参数
results.sort(key=lambda x: x[3])
print("前5个最佳参数组合:")
for i, (p, d, q, aic, bic) in enumerate(results[:5]):
print(f"{i+1}. ARIMA({p},{d},{q}) - AIC: {aic:.4f}, BIC: {bic:.4f}")
print(f"\n最佳参数: ARIMA{best_params} (AIC: {best_aic:.4f})")
self.best_params = best_params
return best_params
def train_model(self, order=None):
"""训练ARIMA模型"""
print(f"\n=== 训练ARIMA模型 ===")
if order is None:
order = self.best_params
if order is None:
print("未指定模型参数")
return None
try:
self.model = ARIMA(self.train_data['CPI'], order=order)
self.fitted_model = self.model.fit()
print(f"使用参数: ARIMA{order}")
print("模型训练完成!")
print(f"AIC: {self.fitted_model.aic:.4f}")
print(f"BIC: {self.fitted_model.bic:.4f}")
print(f"Log Likelihood: {self.fitted_model.llf:.4f}")
return self.fitted_model
except Exception as e:
print(f"模型训练失败: {e}")
return None
def make_predictions(self):
"""进行预测"""
print(f"\n=== 模型预测 ===")
if self.fitted_model is None:
print("模型未训练,无法进行预测")
return None
try:
# 验证集预测(使用滚动预测)
if len(self.val_data) > 0:
val_predictions = []
train_data = self.train_data.copy()
for i in range(len(self.val_data)):
# 使用当前所有数据重新训练模型
current_model = ARIMA(train_data['CPI'], order=self.best_params)
current_fitted = current_model.fit()
# 预测下一个值
next_pred = current_fitted.forecast(steps=1)
val_predictions.append(next_pred[0])
# 添加实际值到训练数据
new_data = pd.DataFrame({'CPI': [self.val_data['CPI'].iloc[i]]},
index=[self.val_data.index[i]])
train_data = pd.concat([train_data, new_data])
self.val_predictions = pd.Series(val_predictions, index=self.val_data.index)
print(f"验证集预测完成,共预测{len(val_predictions)}步")
print(f"验证集预测值范围: [{min(val_predictions):.4f}, {max(val_predictions):.4f}]")
# 测试集预测(使用滚动预测)
if len(self.test_data) > 0:
test_predictions = []
pred_conf_intervals = []
train_val_data = pd.concat([self.train_data, self.val_data])
for i in range(len(self.test_data)):
# 使用当前所有数据重新训练模型
current_model = ARIMA(train_val_data['CPI'], order=self.best_params)
current_fitted = current_model.fit()
# 预测下一个值
forecast = current_fitted.get_forecast(steps=1)
test_predictions.append(forecast.predicted_mean[0])
pred_conf_intervals.append(forecast.conf_int().values[0])
# 添加实际值到训练数据
new_data = pd.DataFrame({'CPI': [self.test_data['CPI'].iloc[i]]},
index=[self.test_data.index[i]])
train_val_data = pd.concat([train_val_data, new_data])
self.predictions = pd.Series(test_predictions, index=self.test_data.index)
self.pred_conf_int = pd.DataFrame(pred_conf_intervals,
columns=['lower CPI', 'upper CPI'],
index=self.test_data.index)
print(f"测试集预测完成,共预测{len(test_predictions)}步")
print(f"测试集预测值范围: [{min(test_predictions):.4f}, {max(test_predictions):.4f}]")
return self.predictions
except Exception as e:
print(f"预测失败: {e}")
return None
def evaluate_model(self):
"""评估模型性能"""
print("\n=== 模型评估 ===")
results = {}
# 评估验证集
if self.val_predictions is not None and len(self.val_data) > 0:
val_actual = self.val_data['CPI'].values
val_pred = self.val_predictions.values
# 确保长度一致
min_len = min(len(val_actual), len(val_pred))
val_actual = val_actual[:min_len]
val_pred = val_pred[:min_len]
# 移除任何无效值
mask = ~(np.isnan(val_actual) | np.isnan(val_pred))
val_actual = val_actual[mask]
val_pred = val_pred[mask]
if len(val_actual) > 0 and len(val_pred) > 0:
val_mse = mean_squared_error(val_actual, val_pred)
val_rmse = np.sqrt(val_mse)
val_mae = mean_absolute_error(val_actual, val_pred)
val_mape = np.mean(np.abs((val_actual - val_pred) / val_actual)) * 100
# 数据诊断
print("\n验证集数据诊断:")
print(f" 数据点数量: {len(val_actual)}")
print(f" 实际值范围: [{np.min(val_actual):.4f}, {np.max(val_actual):.4f}]")
print(f" 预测值范围: [{np.min(val_pred):.4f}, {np.max(val_pred):.4f}]")
print(f" 实际值标准差: {np.std(val_actual):.4f}")
print(f" 预测值标准差: {np.std(val_pred):.4f}")
# 检查是否所有值都相同
if np.std(val_actual) < 1e-10 or np.std(val_pred) < 1e-10:
print(" 警告: 检测到常数序列,这会导致相关系数计算失败")
# 使用更稳健的相关系数计算方法
try:
# 检查数据是否有效
if len(val_actual) < 2 or len(val_pred) < 2:
raise ValueError("数据点数量不足")
# 检查是否存在常数序列
if np.std(val_actual) < 1e-10 or np.std(val_pred) < 1e-10:
raise ValueError("检测到常数序列")
val_pearson_corr, p_value = stats.pearsonr(val_actual, val_pred)
val_spearman_corr, s_p_value = stats.spearmanr(val_actual, val_pred)
val_corr = {
'Pearson': val_pearson_corr,
'Pearson_p_value': p_value,
'Spearman': val_spearman_corr,
'Spearman_p_value': s_p_value
}
print(f" Pearson相关系数 p值: {p_value:.4f}")
print(f" Spearman相关系数 p值: {s_p_value:.4f}")
except Exception as e:
print(f" 相关系数计算失败: {str(e)}")
val_corr = {
'Pearson': np.nan,
'Pearson_p_value': np.nan,
'Spearman': np.nan,
'Spearman_p_value': np.nan
}
results['validation'] = {
'MSE': val_mse,
'RMSE': val_rmse,
'MAE': val_mae,
'MAPE': val_mape,
'Correlation': val_corr
}
print("验证集性能:")
print(f" MSE: {val_mse:.6f}")
print(f" RMSE: {val_rmse:.6f}")
print(f" MAE: {val_mae:.6f}")
print(f" MAPE: {val_mape:.6f}")
print(f" Pearson相关系数: {val_corr['Pearson']:.6f}")
print(f" Spearman相关系数: {val_corr['Spearman']:.6f}")
# 评估测试集
if self.predictions is not None and len(self.test_data) > 0:
test_actual = self.test_data['CPI'].values
test_pred = self.predictions.values
# 确保长度一致
min_len = min(len(test_actual), len(test_pred))
test_actual = test_actual[:min_len]
test_pred = test_pred[:min_len]
# 移除任何无效值
mask = ~(np.isnan(test_actual) | np.isnan(test_pred))
test_actual = test_actual[mask]
test_pred = test_pred[mask]
if len(test_actual) > 0 and len(test_pred) > 0:
test_mse = mean_squared_error(test_actual, test_pred)
test_rmse = np.sqrt(test_mse)
test_mae = mean_absolute_error(test_actual, test_pred)
test_mape = np.mean(np.abs((test_actual - test_pred) / test_actual)) * 100
# 数据诊断
print("\n测试集数据诊断:")
print(f" 数据点数量: {len(test_actual)}")
print(f" 实际值范围: [{np.min(test_actual):.4f}, {np.max(test_actual):.4f}]")
print(f" 预测值范围: [{np.min(test_pred):.4f}, {np.max(test_pred):.4f}]")
print(f" 实际值标准差: {np.std(test_actual):.4f}")
print(f" 预测值标准差: {np.std(test_pred):.4f}")
# 检查是否所有值都相同
if np.std(test_actual) < 1e-10 or np.std(test_pred) < 1e-10:
print(" 警告: 检测到常数序列,这会导致相关系数计算失败")
# 使用更稳健的相关系数计算方法
try:
# 检查数据是否有效
if len(test_actual) < 2 or len(test_pred) < 2:
raise ValueError("数据点数量不足")
# 检查是否存在常数序列
if np.std(test_actual) < 1e-10 or np.std(test_pred) < 1e-10:
raise ValueError("检测到常数序列")
test_pearson_corr, p_value = stats.pearsonr(test_actual, test_pred)
test_spearman_corr, s_p_value = stats.spearmanr(test_actual, test_pred)
test_corr = {
'Pearson': test_pearson_corr,
'Pearson_p_value': p_value,
'Spearman': test_spearman_corr,
'Spearman_p_value': s_p_value
}
print(f" Pearson相关系数 p值: {p_value:.4f}")
print(f" Spearman相关系数 p值: {s_p_value:.4f}")
except Exception as e:
print(f" 相关系数计算失败: {str(e)}")
test_corr = {
'Pearson': np.nan,
'Pearson_p_value': np.nan,
'Spearman': np.nan,
'Spearman_p_value': np.nan
}
# 方向准确率
if len(test_actual) > 1:
actual_direction = np.diff(test_actual) > 0
predicted_direction = np.diff(test_pred) > 0
direction_accuracy = np.mean(actual_direction == predicted_direction) * 100
else:
direction_accuracy = np.nan
results['test'] = {
'MSE': test_mse,
'RMSE': test_rmse,
'MAE': test_mae,
'MAPE': test_mape,
'Correlation': test_corr,
'Direction_Accuracy': direction_accuracy
}
print("\n测试集性能:")
print(f" MSE: {test_mse:.6f}")
print(f" RMSE: {test_rmse:.6f}")
print(f" MAE: {test_mae:.6f}")
print(f" MAPE: {test_mape:.6f}")
print(f" Pearson相关系数: {test_corr['Pearson']:.6f}")
print(f" Spearman相关系数: {test_corr['Spearman']:.6f}")
print(f" 方向准确率: {direction_accuracy:.6f}%")
return results
def model_diagnostics(self):
"""模型诊断"""
print("\n=== 模型诊断 ===")
if self.fitted_model is None:
print("模型未训练,无法进行诊断")
return
# 残差分析
residuals = self.fitted_model.resid
# 计算标准化残差
std_residuals = residuals / residuals.std()
fig, axes = plt.subplots(2, 2, figsize=(15, 10))
# 残差时序图
axes[0, 0].plot(residuals.index, residuals, linewidth=1.5)
axes[0, 0].axhline(y=0, color='red', linestyle='--', alpha=0.7)
axes[0, 0].set_title('Residuals Time Series')
axes[0, 0].set_xlabel('Time')
axes[0, 0].set_ylabel('Residuals')
axes[0, 0].grid(True, alpha=0.3)
# 标准化残差直方图
axes[0, 1].hist(std_residuals, bins=20, alpha=0.7, color='skyblue', edgecolor='black')
axes[0, 1].axvline(x=0, color='red', linestyle='--', alpha=0.7)
axes[0, 1].set_title('Standardized Residuals Histogram')
axes[0, 1].set_xlabel('Standardized Residuals')
axes[0, 1].set_ylabel('Frequency')
axes[0, 1].grid(True, alpha=0.3)
# 残差ACF
try:
plot_acf(residuals, ax=axes[1, 0], lags=min(20, len(residuals)//4))
axes[1, 0].set_title('Residuals ACF')
except:
axes[1, 0].text(0.5, 0.5, 'ACF plot failed', transform=axes[1, 0].transAxes, ha='center')
# 残差Q-Q图
try:
stats.probplot(std_residuals, dist="norm", plot=axes[1, 1])
axes[1, 1].set_title('Q-Q Plot (Standardized Residuals)')
axes[1, 1].grid(True, alpha=0.3)
except:
axes[1, 1].text(0.5, 0.5, 'Q-Q plot failed', transform=axes[1, 1].transAxes, ha='center')
plt.tight_layout()
plt.savefig('model_diagnostics.png', dpi=300, bbox_inches='tight')
plt.show()
# 统计检验
print("\n诊断统计:")
print(f"残差均值: {residuals.mean():.6f}")
print(f"残差标准差: {residuals.std():.6f}")
print(f"残差偏度: {stats.skew(residuals):.6f}")
print(f"残差峰度: {stats.kurtosis(residuals):.6f}")
# Ljung-Box检验
try:
max_lags = min(10, len(residuals)//4)
lb_test = acorr_ljungbox(residuals, lags=max_lags, return_df=True)
print(f"\nLjung-Box检验 (残差独立性, lags={max_lags}):")
print(lb_test.head())
except Exception as e:
print(f"Ljung-Box检验失败: {e}")
# Jarque-Bera检验
try:
jb_stat, jb_pvalue = stats.jarque_bera(residuals)
print(f"\nJarque-Bera检验 (正态性): 统计量={jb_stat:.4f}, p值={jb_pvalue:.4f}")
if jb_pvalue < 0.05:
print("残差不服从正态分布 (p值 < 0.05)")
else:
print("残差服从正态分布 (p值 >= 0.05)")
except Exception as e:
print(f"Jarque-Bera检验失败: {e}")
def plot_prediction_results(self):
"""绘制预测结果"""
if self.predictions is None:
print("未进行预测,无法绘制结果")
return
fig, axes = plt.subplots(2, 1, figsize=(15, 12))
# 预测结果对比
axes[0].plot(self.train_data.index, self.train_data['CPI'],
label='Training Data', linewidth=2, color='blue')
if len(self.val_data) > 0 and self.val_predictions is not None:
axes[0].plot(self.val_data.index, self.val_data['CPI'],
label='Validation Actual', linewidth=2, color='orange')
# 确保预测数据长度与验证数据一致
val_pred_len = min(len(self.val_data), len(self.val_predictions))
axes[0].plot(self.val_data.index[:val_pred_len], self.val_predictions[:val_pred_len],
label='Validation Predicted', linewidth=2, color='red', linestyle=':')
if len(self.test_data) > 0:
axes[0].plot(self.test_data.index, self.test_data['CPI'],
label='Test Actual', linewidth=2, color='green')
# 确保预测数据长度与测试数据一致
test_pred_len = min(len(self.test_data), len(self.predictions))
axes[0].plot(self.test_data.index[:test_pred_len], self.predictions[:test_pred_len],
label='Test Predicted', linewidth=2, color='purple', linestyle='--')
# 添加置信区间
if hasattr(self, 'pred_conf_int'):
axes[0].fill_between(self.test_data.index[:test_pred_len],
self.pred_conf_int.iloc[:test_pred_len, 0],
self.pred_conf_int.iloc[:test_pred_len, 1],
alpha=0.3, color='purple', label='95% Confidence Interval')
axes[0].set_title('CPI Prediction Results')
axes[0].set_xlabel('Time')
axes[0].set_ylabel('CPI Index')
axes[0].legend()
axes[0].grid(True, alpha=0.3)
# 预测误差分析
if len(self.test_data) > 0 and self.predictions is not None:
test_pred_len = min(len(self.test_data), len(self.predictions))
errors = self.test_data['CPI'][:test_pred_len] - self.predictions[:test_pred_len]
axes[1].plot(self.test_data.index[:test_pred_len], errors,
linewidth=2, color='red', marker='o', markersize=4)
axes[1].axhline(y=0, color='black', linestyle='-', alpha=0.5)
axes[1].fill_between(self.test_data.index[:test_pred_len], errors, 0,
alpha=0.3, color='red')
axes[1].set_title('Test Set Prediction Errors')
axes[1].set_xlabel('Time')
axes[1].set_ylabel('Error Value')
axes[1].grid(True, alpha=0.3)
plt.tight_layout()
plt.savefig('prediction_results.png', dpi=300, bbox_inches='tight')
plt.show()
def time_series_cross_validation(self, initial_train_size=None, step_size=1):
"""修复的时间序列交叉验证"""
print("\n=== 时间序列交叉验证 ===")
if self.best_params is None:
print("未找到最佳参数,无法进行交叉验证")
return [], []
if initial_train_size is None:
initial_train_size = max(20, int(len(self.data) * 0.4))
cv_scores = []
successful_validations = 0
# 确保有足够的数据进行交叉验证
max_iterations = min(10, len(self.data) - initial_train_size - step_size)
for i in range(max_iterations):
try:
end_idx = initial_train_size + i * step_size
if end_idx + step_size >= len(self.data):
break
train_cv = self.data.iloc[:end_idx]
test_cv = self.data.iloc[end_idx:end_idx + step_size]
if len(train_cv) < 10 or len(test_cv) == 0:
continue
# 训练模型
model = ARIMA(train_cv['CPI'], order=self.best_params)
fitted_model = model.fit()
# 预测
pred = fitted_model.forecast(steps=step_size)
# 计算误差
if len(pred) > 0 and len(test_cv) > 0:
actual_values = test_cv['CPI'].values
pred_values = pred if isinstance(pred, np.ndarray) else pred.values
# 确保长度一致
min_len = min(len(actual_values), len(pred_values))
if min_len > 0:
mse = mean_squared_error(actual_values[:min_len], pred_values[:min_len])
cv_scores.append(mse)
successful_validations += 1
except Exception as e:
print(f"交叉验证第{i+1}次失败: {e}")
continue
if successful_validations > 0:
print(f"交叉验证完成,成功验证{successful_validations}次")
print(f"*均MSE: {np.mean(cv_scores):.6f}")
print(f"MSE标准差: {np.std(cv_scores):.6f}")
print(f"最小MSE: {np.min(cv_scores):.6f}")
print(f"最大MSE: {np.max(cv_scores):.6f}")
else:
print("交叉验证全部失败")
return cv_scores, successful_validations
def forecast_future(self, periods=12):
"""改进的未来预测函数"""
print(f"\n=== 未来{periods}期预测 ===")
if self.fitted_model is None:
print("模型未训练,无法进行未来预测")
return None
try:
# 检查模型稳定性
if hasattr(self.fitted_model, 'arroots'):
ar_roots = self.fitted_model.arroots
if len(ar_roots) > 0 and np.any(np.abs(ar_roots) <= 1.01):
print("警告:模型可能不稳定,重新训练...")
# 使用更保守的参数重新训练
conservative_order = (1, 1, 1)
temp_model = ARIMA(self.data['CPI'], order=conservative_order)
fitted_model = temp_model.fit()
else:
fitted_model = self.fitted_model
else:
fitted_model = self.fitted_model
# 使用step-by-step预测方法
future_predictions = []
future_conf_intervals = []
# 准备预测数据
current_data = self.data['CPI'].copy()
for step in range(periods):
try:
# 单步预测
forecast_result = fitted_model.get_forecast(steps=1)
pred_value = forecast_result.predicted_mean.iloc[0]
conf_int = forecast_result.conf_int()
# 检查预测值是否有效
if np.isnan(pred_value) or np.isinf(pred_value):
# 使用简单的趋势外推
recent_values = current_data.tail(6).values
if len(recent_values) >= 2:
trend = np.mean(np.diff(recent_values))
pred_value = current_data.iloc[-1] + trend
# 设置保守的置信区间
lower_bound = pred_value - 2 * np.std(recent_values)
upper_bound = pred_value + 2 * np.std(recent_values)
else:
pred_value = current_data.iloc[-1]
lower_bound = pred_value - 1
upper_bound = pred_value + 1
else:
lower_bound = conf_int.iloc[0, 0]
upper_bound = conf_int.iloc[0, 1]
future_predictions.append(pred_value)
future_conf_intervals.append([lower_bound, upper_bound])
# 更新数据以进行下一步预测
new_data = pd.Series([pred_value], index=[current_data.index[-1] + pd.DateOffset(months=1)])
current_data = pd.concat([current_data, new_data])
# 重新拟合模型(可选,用于多步预测)
if step < periods - 1:
fitted_model = ARIMA(current_data, order=self.best_params).fit()
except Exception as e:
print(f"第{step+1}步预测失败:{e}")
# 使用线性外推作为备用方案
if len(future_predictions) > 0:
pred_value = future_predictions[-1]
else:
pred_value = current_data.iloc[-1]
future_predictions.append(pred_value)
future_conf_intervals.append([pred_value - 1, pred_value + 1])
# 创建未来日期
last_date = self.data.index[-1]
future_dates = pd.date_range(start=last_date + pd.DateOffset(months=1),
periods=periods, freq='M')
# 创建结果DataFrame
future_df = pd.DataFrame({
'预测CPI': future_predictions,
'下界': [ci[0] for ci in future_conf_intervals],
'上界': [ci[1] for ci in future_conf_intervals]
}, index=future_dates)
print("未来预测结果:")
print(future_df.round(4))
return future_df
except Exception as e:
print(f"未来预测失败: {e}")
# 提供备用预测方案
return self.backup_forecast(periods)
def backup_forecast(self, periods=12):
"""备用预测方案"""
print("使用备用预测方案...")
# 基于历史趋势的简单预测
recent_data = self.data['CPI'].tail(12)
# 计算趋势
trend = np.polyfit(range(len(recent_data)), recent_data.values, 1)[0]
# 计算季节性(如果数据足够)
if len(self.data) >= 24:
seasonal_component = []
for i in range(12):
monthly_values = []
for j in range(i, len(self.data), 12):
monthly_values.append(self.data['CPI'].iloc[j])
seasonal_component.append(np.mean(monthly_values) - self.data['CPI'].mean())
else:
seasonal_component = [0] * 12
# 生成预测
last_value = self.data['CPI'].iloc[-1]
future_predictions = []
for i in range(periods):
seasonal_adj = seasonal_component[i % 12]
pred_value = last_value + trend * (i + 1) + seasonal_adj
future_predictions.append(pred_value)
# 创建未来日期
last_date = self.data.index[-1]
future_dates = pd.date_range(start=last_date + pd.DateOffset(months=1),
periods=periods, freq='M')
# 计算置信区间
std_dev = self.data['CPI'].std()
future_df = pd.DataFrame({
'预测CPI': future_predictions,
'下界': [pred - 2*std_dev for pred in future_predictions],
'上界': [pred + 2*std_dev for pred in future_predictions]
}, index=future_dates)
return future_df
def run_complete_analysis(self):
"""运行完整的分析流程"""
print("=" * 60)
print("改进的中国居民消费价格指数预测分析")
print("=" * 60)
try:
# 1. 加载数据
if self.load_data() is None:
return None
# 2. *稳性检验
self.is_stationary = self.check_stationarity(self.data['CPI'])
# 3. 分割数据
self.split_data()
# 4. 寻找最佳参数
best_params = self.find_best_arima_params()
if best_params is None:
print("未找到合适的ARIMA参数")
return None
# 5. 训练模型
if self.train_model() is None:
return None
# 6. 进行预测
if self.make_predictions() is None:
return None
# 7. 评估模型
metrics = self.evaluate_model()
# 8. 模型诊断
self.model_diagnostics()
# 9. 交叉验证
cv_scores, successful_validations = self.time_series_cross_validation()
# 10. 绘制结果
self.plot_prediction_results()
# 11. 未来预测
future_forecast = self.forecast_future(periods=12)
print("\n" + "=" * 60)
print("分析完成!")
print("=" * 60)
return {
'model': self.fitted_model,
'predictions': self.predictions,
'val_predictions': self.val_predictions,
'metrics': metrics,
'cv_scores': cv_scores,
'successful_validations': successful_validations,
'future_forecast': future_forecast,
'best_params': self.best_params
}
except Exception as e:
print(f"分析过程中发生错误: {e}")
import traceback
traceback.print_exc()
return None
if __name__ == "__main__":
# 创建预测器实例
predictor = ImprovedCPIPredictor('CPI数据集.txt')
# 运行完整分析
results = predictor.run_complete_analysis()
if results:
print("\n分析成功完成!")
print(f"最佳ARIMA参数: {results['best_params']}")
if results['successful_validations'] > 0:
print(f"交叉验证成功次数: {results['successful_validations']}")
print("结果已保存到图片文件")
else:
print("分析失败,请检查数据和参数")
log
(base) root@ubuntu22:~# python Arima.py
============================================================
改进的中国居民消费价格指数预测分析
============================================================
正在加载CPI数据...
数据加载完成,共85条记录
时间范围:2018-06-01 00:00:00 到 2025-06-01 00:00:00
数据基本统计信息:
CPI
count 85.000000
mean 101.414118
std 1.402222
min 99.200000
25% 100.200000
50% 101.300000
75% 102.400000
max 105.400000
=== *稳性检验 ===
ADF统计量: -0.7200
p值: 0.8415
临界值:
1%: -3.5246
5%: -2.9026
10%: -2.5887
结论: 时间序列不是*稳的 (p值 >= 0.05)
尝试1阶差分...
差分后ADF统计量: -3.7427
差分后p值: 0.0036
经过1阶差分后,时间序列变得*稳 (p值 < 0.05)
=== 数据分割 ===
训练集: 51 条记录
验证集: 17 条记录
测试集: 17 条记录
=== 寻找最佳ARIMA参数 ===
使用已确定的差分阶数: d = 1
找到更好的参数: ARIMA(0, 1, 0) (AIC: 79.0894)
找到更好的参数: ARIMA(0, 1, 1) (AIC: 71.7730)
前5个最佳参数组合:
1. ARIMA(0,1,1) - AIC: 71.7730, BIC: 75.5971
2. ARIMA(1,1,0) - AIC: 73.4236, BIC: 77.2477
3. ARIMA(2,1,0) - AIC: 73.6203, BIC: 79.3563
4. ARIMA(1,1,2) - AIC: 73.7416, BIC: 81.3897
5. ARIMA(1,1,1) - AIC: 73.7727, BIC: 79.5088
最佳参数: ARIMA(0, 1, 1) (AIC: 71.7730)
=== 训练ARIMA模型 ===
使用参数: ARIMA(0, 1, 1)
模型训练完成!
AIC: 71.7730
BIC: 75.5971
Log Likelihood: -33.8865
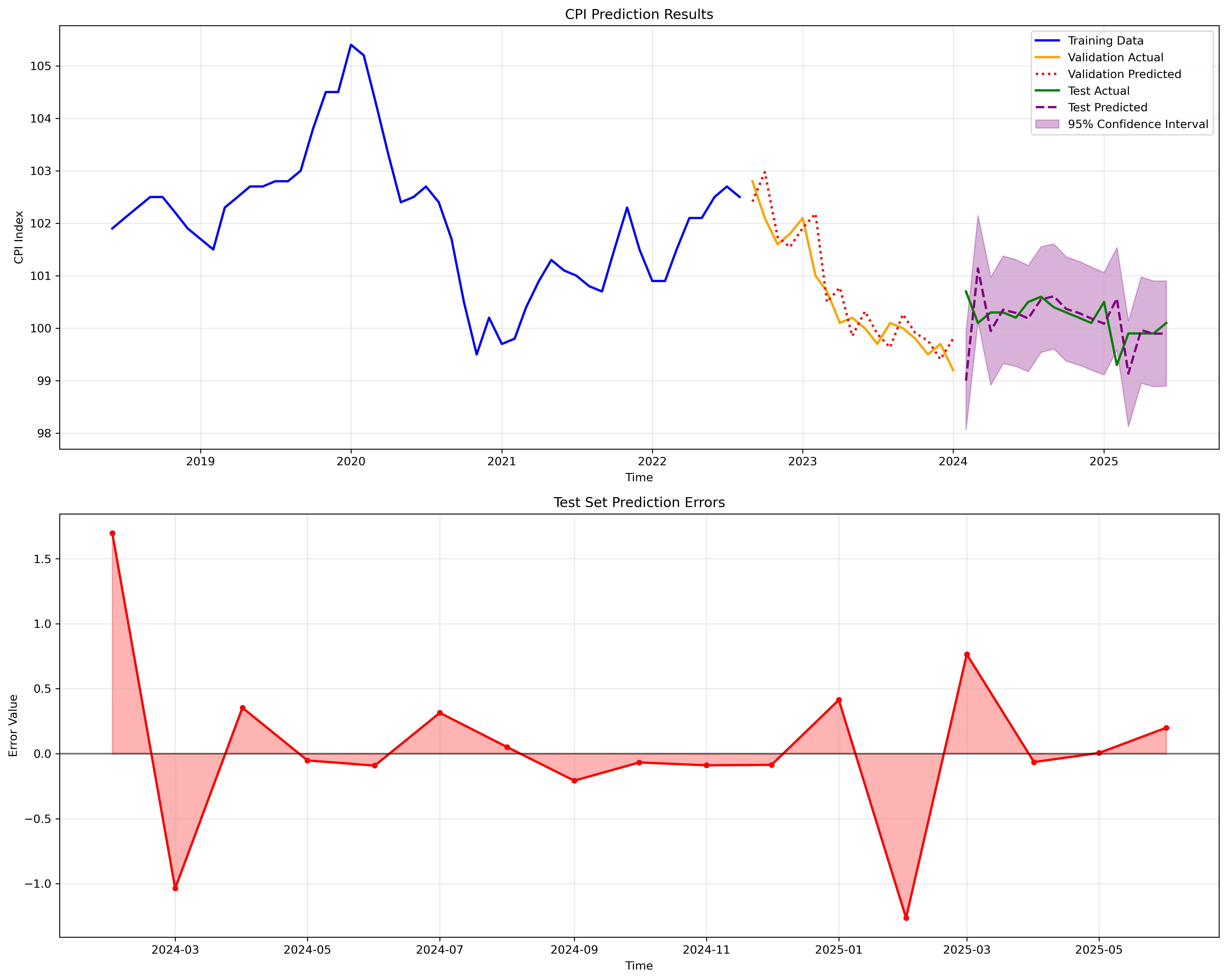
=== 模型预测 ===
验证集预测完成,共预测17步
验证集预测值范围: [99.4080, 102.9743]
测试集预测完成,共预测17步
测试集预测值范围: [99.0019, 101.1368]
=== 模型评估 ===
验证集数据诊断:
数据点数量: 17
实际值范围: [99.2000, 102.8000]
预测值范围: [99.4080, 102.9743]
实际值标准差: 1.0504
预测值标准差: 1.0950
Pearson相关系数 p值: 0.0000
Spearman相关系数 p值: 0.0000
验证集性能:
MSE: 0.235670
RMSE: 0.485458
MAE: 0.397730
MAPE: 0.395008
Pearson相关系数: 0.907641
Spearman相关系数: 0.842754
测试集数据诊断:
数据点数量: 17
实际值范围: [99.3000, 100.7000]
预测值范围: [99.0019, 101.1368]
实际值标准差: 0.3226
预测值标准差: 0.4971
Pearson相关系数 p值: 0.6500
Spearman相关系数 p值: 0.8064
测试集性能:
MSE: 0.391682
RMSE: 0.625845
MAE: 0.397762
MAPE: 0.397179
Pearson相关系数: -0.118703
Spearman相关系数: 0.064279
方向准确率: 43.750000%
=== 模型诊断 ===
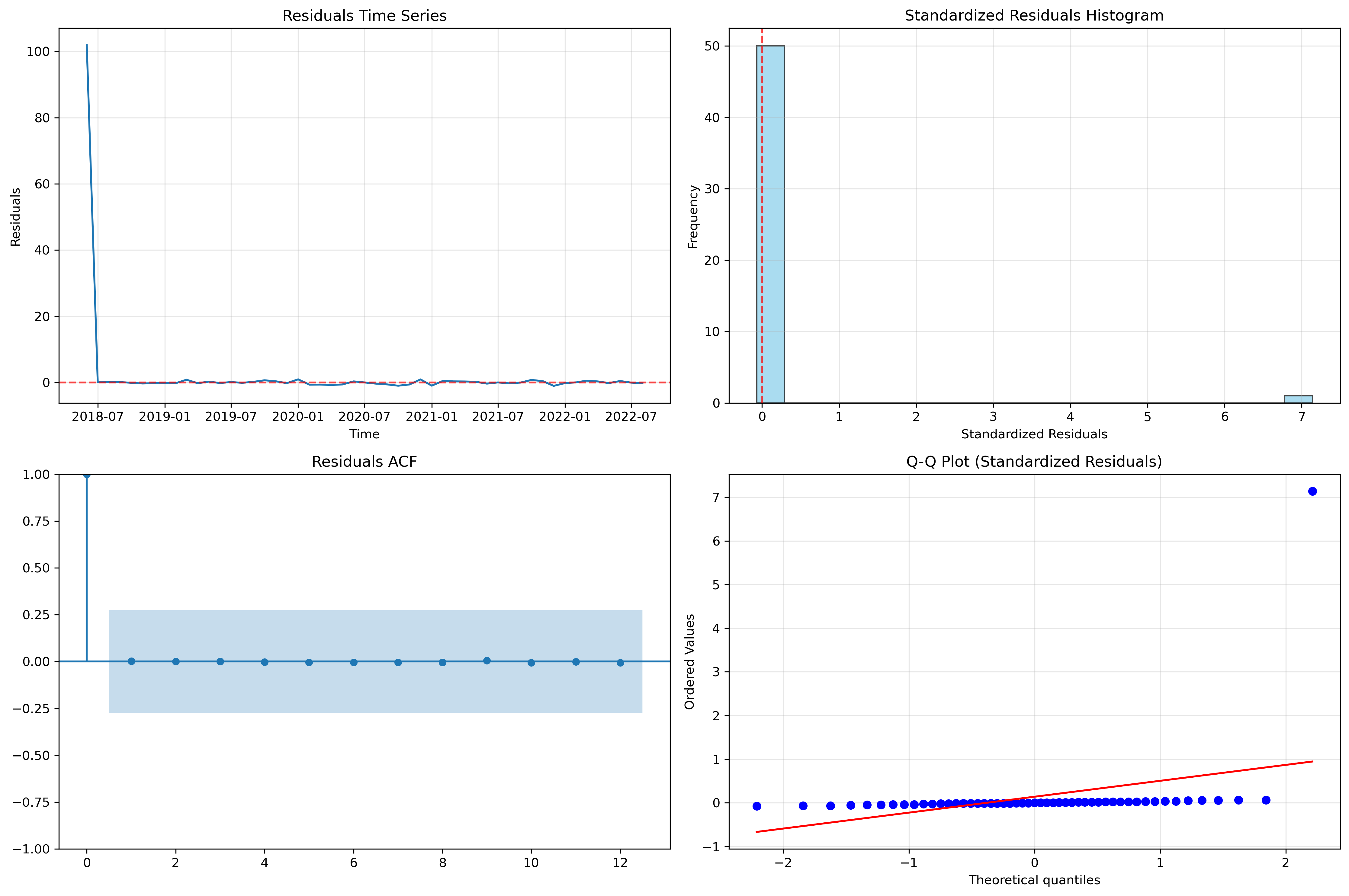
诊断统计:
残差均值: 2.005193
残差标准差: 14.275755
残差偏度: 6.917642
残差峰度: 45.911405
Ljung-Box检验 (残差独立性, lags=10):
lb_stat lb_pvalue
1 0.000122 0.991180
2 0.000131 0.999935
3 0.000134 1.000000
4 0.000454 1.000000
5 0.001639 1.000000
Jarque-Bera检验 (正态性): 统计量=4885.9534, p值=0.0000
残差不服从正态分布 (p值 < 0.05)
=== 时间序列交叉验证 ===
交叉验证完成,成功验证10次
*均MSE: 0.221902
MSE标准差: 0.315458
最小MSE: 0.000273
最大MSE: 0.992711
=== 未来12期预测 ===
未来预测结果:
预测CPI 下界 上界
2025-07-31 102.4122 101.4803 103.3440
2025-08-31 102.6559 101.5529 103.7589
2025-09-30 102.6559 101.5593 103.7525
2025-10-31 102.6559 101.5656 103.7461
2025-11-30 102.6559 101.5718 103.7399
2025-12-31 102.6559 101.5779 103.7338
2026-01-31 102.6559 101.5839 103.7278
2026-02-28 102.6559 101.5899 103.7219
2026-03-31 102.6559 101.5957 103.7161
2026-04-30 102.6559 101.6014 103.7104
2026-05-31 102.6559 101.6070 103.7048
2026-06-30 102.6559 101.6125 103.6992
============================================================
分析完成!
============================================================
分析成功完成!
最佳ARIMA参数: (0, 1, 1)
交叉验证成功次数: 10
结果已保存到图片文件

 浙公网安备 33010602011771号
浙公网安备 33010602011771号