数据结构 | 栈(Stack)
栈(Stack)是一个数据集合,可以理解为只能在一端进行插入或删除操作的列表。
栈的特点:后进先出(last-in, first-out)
栈可以分为
- 顺序栈: 数组实现
- 链式栈: 链表实现
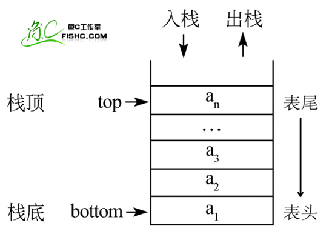
栈的概念:
- 栈顶
- 栈底
栈的空间复杂度:
有一个n个元素的栈, 在入栈和出栈过程中, 只需要存储一个临时变量存储空间, 所以空间复杂度是O(1)
并不是说栈有n个元素, 空间复杂度就是O(n), 而是指除了原本的空间外, 算法需要的额外空间
一、栈的线性表实现
- 线性表,后端插入和删除的时间复杂度是O(1),表尾作为栈顶;
- 链接表,前端插入和删除的时间复杂度是O(1),表首作为栈顶;
1.栈的顺序表实现
栈的基本操作
- 进栈(压栈):push
- 出栈:pop
- 取栈顶:top
- 判断为空:isEmpty
- 返回栈大小:size
先定义一个异常类
class StackUnderFlow(ValueError): pass
class SStack: def __init__(self): self._elems = [] # 先在初始化函数里面定义一个空列表 def is_empty(self): return self._elems == [] def size(self): return len(self._elems) def push(self, elem): self._elems.append(elem) def pop(self): if self.is_empty(): raise StackUnderFlow(" in SStack.pop()") return self._elems.pop() def top(self): if self.is_empty(): raise StackUnderFlow(" in SStack.top()") return self._elems[-1]
- pop和peek函数都有先检查栈是否为空的情况,否则会报错;
栈的reverse
思路:把所有元素按照原来的顺序全部入栈,再顺序取出,就能得到反序后的序列
st = SStack() for i in lis: st.push(i) lis = [] while not st.is_empty: lis.append(st.pop())
2.栈的链接表实现
class LStack: def __init__(self): self._top = None def is_empty(self): return self._top == None def push(self,elem): self._top = LNode(elem,self._top) def pop(self): if self.is_empty(): raise StackUnderFlow("in LStack.pop()") p = self._top.elem self._top = p.next return p def top(self,elem): if self.is_empty(): raise StackUnderFlow("in LStack.top()") return self._top.elem
二、 栈的应用
1. 括号匹配问题
给一个字符串,其中包含小括号、中括号、大括号,求该字符串中的括号是否匹配。
def check_parentheses(text): open_parens = "([{" parens = "([{}])" opposite = { ')':'(', ']':'[','}':'{'} def parentheses(text): i,n = 0, len(text) while True: while i<n and text[i] not in parens: i += 1 if i >= n: return yield text[i],i i += 1 st = SStack() for pr,i in parentheses(text): if pr in open_parens: st.push(pr) elif st.pop() != opposite[pr]: pass else: return False print("all parentheses are correctly matched") return True text = "test([{test}])" print(check_parentheses(text)) ''' all parentheses are correctly matched True '''
2. 求二进制
如数字6(110), 分别用2除6, 求余数, 最后余数反转就是110(先除2求余,再整除2)
def binary(num): s = SStack() while num > 0: n = num % 2 s.push(n) num = num // 2 # 反转 res = "" while not s.isEmpty(): res += str(s.pop()) # 栈是后进后出,一个个pop出来就是倒序的,转成字符串 return res if __name__ == "__main__": assert binary(5) == '101' assert binary(8) == '1000' assert binary(9) == '1001'
divmod:计算除数和被除数的结果,并返回一个包含商和余数的元组。但是会使速度变慢。
n,num = divmod(num, 2)
divmod(5,2) # (2,1)
三、 栈与递归
将递归转换为非递归,只需要一个栈保存递归函数执行时每层调用的局部信息。
递归
def fact(n): if n == 0: return 1 else: return n * fact(n-1)
非递归
def norec_fact(n): st = SStack() res = 1 while n>0: st.push(n) n -= 1 while not st.is_empty(): res *= st.pop() return res
简单背包问题
假设有n件质量分配为w1,w2,…,wn的物品和一个最多能装载总质量为maxW的背包,能否从这n件物品中选择若干件物品装入背包,使得被选物品的总质量“恰好”等于背包所能装载的最大质量,即wi1+wi2+…+wik=maxW。若能,则背包问题有解,否则无解。
def knap_rec(weight,wlist,n) : if weight == 0 : return True if weight < 0 or (weight >0 and n < 1) : return False if knap_rec(weight - wlist[n-1],wlist,n-1) : print("Item" + str(n) + ":" , wlist[n-1]) return True if knap_rec(weight,wlist,n-1) : return True else : return False
拓展:栈的Python实现
不需要自己定义,使用列表结构即可。
- 进栈函数:append
- 出栈函数:pop
- 查看栈顶函数:li[-1]
进栈顺序是ABC,哪个不可能是它的出栈顺序。
ABC
ABC A进A出,B进B出,C进C出
ACB A进A出,B进C进,C出B出
BCA A进栈,B进栈,B出栈,C进栈,C出栈,A出栈
BAC A进栈,B进栈,B出栈,A出栈,C进栈,C出栈
CBA A进栈,B进栈,C进栈,C出栈,B出栈,A出栈
CAB
n个元素序列的合法出栈顺序有多少种?就是卡特兰数的第n项。
卡特兰数又称卡塔兰数,英文名Catalan number,是组合数学中一个常出现在各种计数问题中出现的数列。以比利时的数学家欧仁·查理·卡塔兰 (1814–1894)的名字来命名,其前几项为(从第零项开始) : 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, ...


 浙公网安备 33010602011771号
浙公网安备 33010602011771号