数据结构 | 顺序表

 

什么是数据结构？

　　数据结构是指相互之间存在着一种或多种关系的数据元素的集合和该集合中数据元素之间的关系组成。 简单来说，数据结构就是设计数据以何种方式组织并存储在计算机中。 比如：列表、集合与字典等都是一种数据结构。

N.Wirth: “程序=数据结构+算法”

 

数据结构的分类

数据结构按照其逻辑结构可分为线性结构、树结构、图结构

• 线性结构：数据结构中的元素存在一对一的相互关系
• 树结构：数据结构中的元素存在一对多的相互关系
• 图结构：数据结构中的元素存在多对多的相互关系

  

线性结构/线性表

• 顺序表
• 链表

 

顺序表

1. 列表 / 数组

动态数组也称数组列表，在python中一般为List。

列表：在其他编程语言中称为“数组”，是一种基本的数据结构类型。列表又叫做顺序表（连续存储的方式）。

 

数组的缺点是大小固定, 一旦声明长度就要占用连续的内存空间, 当空间不够用时更换更大的空间, 此时就需要将原数组的所有数据迁移过去, 比较费时。

 

• 顺序存储数据
• 连续存储
• 任意顺序访问，可变大小的列表数据结构允许增加、删除元素

 

2. 数组操作函数：

 

3. 数组内置操作函数的时间复杂度

 

 

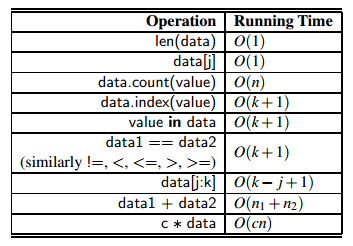
4.用python实现内置函数的方法

class DynamicArray:

    def __init__(self):
        'Create an empty array.'
        self._n = 0                                     # size
        self._capacity = 10                             # 先给个10
        self._A = self._make_array(self._capacity)

    def __len__(self):
        return self._n

    def is_empty(self):
        return self._n == 0

    # O(1)
    def __getitem__(self, k):
        if not 0 <= k < self._n:
            raise ValueError('invalid index')
        return self._A[k]

    # O(1)
    def append(self, obj):
        if self._n == self._capacity:           # 首先要判断该容器是否放得下
            self._resize(2 * self._capacity)
        self._A[self._n] = obj
        self._n += 1

    def _make_array(self, c):
        return (c * ctypes.py_object)()

    def _resize(self, c):
        B = self._make_array(c)
        for k in range(self._n):
            B[k] = self._A[k]
        self._A = B
        self._capacity = c

    # O(n)
    def insert(self, k, value):
        if self._n == self._capacity:
            self._resize(2 * self._capacity)
        for j in range(self._n, k, -1):             # 从后往前一个一个往后移
            self._A[j] = self._A[j - 1]
        self._A[k] = value
        self._n += 1

    # O(n)
    def remove(self, value):
        for k in range(self._n):
            if self._A[k] == value:                 # 一个个查value
                for j in range(k, self._n - 1):
                    self._A[j] = self._A[j + 1]     # 再一个个移上来
                self._A[self._n - 1] = None
                self._n -= 1
                return
        raise ValueError('value not found')

    def _print(self):
        for i in range(self._n):
            print(self._A[i], end=' ')
        print()

• 在append和insert函数里面，要先判断是否超出给定的capacity，如果超出，要扩容resize扩容；
• insert时，从后往前找，remove的时候从前往后找，然后找到之后，将后面的元素一一往前移动 self._A[j] = self._A[j + 1]，最后一个元素赋值为None，然后总n-1；
• __getitem__ 当访问元素时会调用该方法li[i]

 

5. list进行reverse

复杂度 O(n)

def reverse(list):
    i, j = 0, len(list)-1
    while i<j:
        list[i],list[j] = list[j],list[i]
        i += 1
        j -= 1

    return list

li = [1,2,3,4,5,6]
print(reverse(li))

'''
[6, 5, 4, 3, 2, 1]
'''

 注意：因为下标从0开始，所以len后要减1

 

def reverse(self):
    elems = self.elements
    i, j = 0, len(elems)-1
    while i<j:
        elems[i],elems[j] = elems[j],elems[i]
        i, j = i+1,j-1

注意：写法

 

6. 关于列表的问题

• 列表中元素使如何存储的？
• 列表提供了哪些基本的操作？
• 这些操作的时间复杂度是多少？append是O(1)；插入和删除是O(n)

扩展：Python的列表是如何实现的？

其他语言中的数组：一个整数占4个字节（bytes）, 假设有一个数组a，在内存中会记录它的起始点300处，找a[2]就是300+2*4=308

 

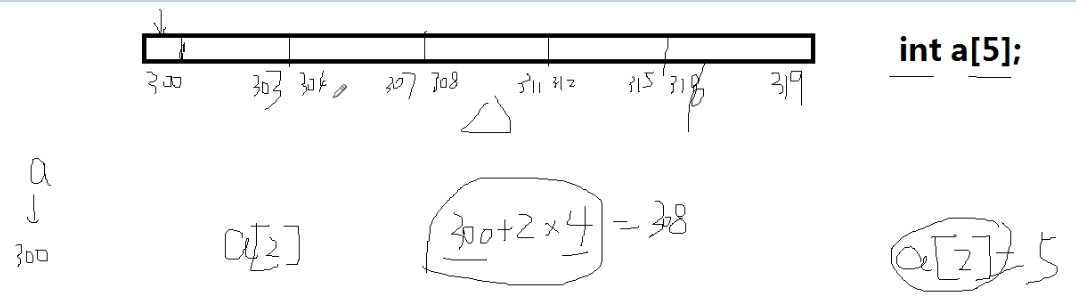
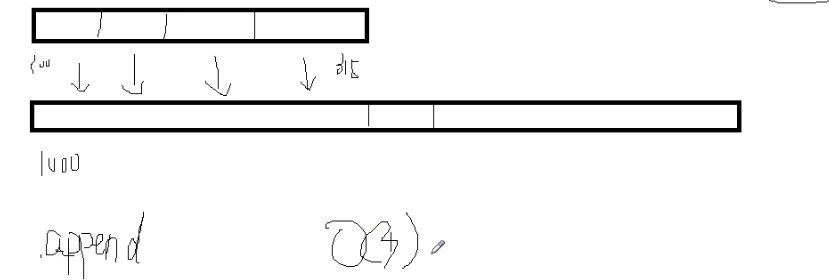
python中的列表，如何解决append的问题呢？

会在后面的内存中开辟一个比append前长一倍的内存，然后，将前面的元素全部复制过去。

 

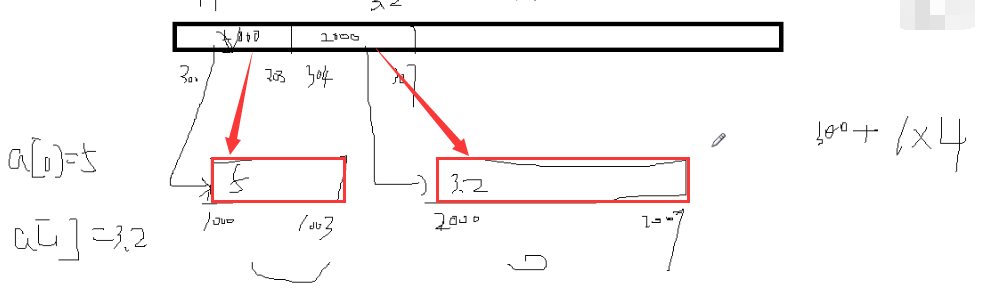
如何解决数据类型不一样的问题，因为数据类型不一样，占用的内存就不一样，就不好去计算。

另外开辟一段内存来存放真实数据。仍然通过之前的方式找到数据所在地址，比如找a[1]，就通过300+4*1找到304，304处存放的是真实数据所在的内存地址2000，通过二次寻址的方式，找到真实数据2000处存放的是3.2。