PTA第二次BLOG
一、前言
-
PTA题目集4:还是和PTA3(PTA题目集3,后面都省略这样写)一样的味道,各种建立类,然后通过类对象调用其中的方法,就很经典的面向对象编程。和PTA3大同小异。为啥这么说嘞?主要是解决问题的方式和PTA3差不多,拿着PTA3的代码,然后新建立一个四边形类,又是构建里面的判断方法,get,set等方法,只不过对象变成了四边形而已。多了一点步骤。难度其实还可以,但是在经历了PTA3之后,有了之前写好的一些类,确实简单了不少。这里说的都是第二题,一,三题的话相对于第二题都属于轻量级别,当然并不是说他们一点难度没有,只是没有第二题那么多题量,简单解决一个问题就可以。
-
PTA题目集5:相对于PTA4在PTA3上添加一个四边形类,PTA5我可以说是把整个代码重构了一遍了,因为可以用到继承以及多态,而且很明显就能够发现三边形,四边形,五边形可以找到共同点,也就是多边形。然后就到了苦逼的重构时间了,写了一个新类,把点,边,求面积,求周长(还有其他,这里没写)等等属性和方法全部放进去了,然后三角形类,四边形类,五边形类都继承这个类。这样一来,代码直接少了一大截。PTA4的时候已经1000多行代码了,PTA5又要加一个五边形类,但到最后写完题目的时候总共才500多行(只能说继承和多态YYDS),是真的很舒服,而且如果有六边形,七边形也能直接继承多边形,拓展性MAX好吧(我现在是这么认为,希望之后别打脸AWA)。重构完之后其实就会觉得题目并不是那么难,因为很多方法无论是三角形,四边形,五边形直接调用就行,不用分那么多情况。当然,虽然这么说,但是题目是真的多(TWT)
-
期中考试:其中测试的话其实不算难,因为题目中已经给了类图,说的直白点,几乎是把答案糊在脸上了。但是前提是要能理解继承和多态,这样写起来才顺畅,不然就算对着类图照抄也抄的很迷离。个人认为期中测试主要是测试我们对对象概念的理解,对继承和多态的能否实现简单应用,over!
二、设计与分析
PTA题目集4——点线形系列4-凸四边形的计算
-
题目内容
用户输入一组选项和数据,进行与四边形有关的计算。
以下四边形顶点的坐标要求按顺序依次输入,连续输入的两个顶点是相邻顶点,第一个和最后一个输入的顶点相邻。
选项包括:
1:输入四个点坐标,判断是否是四边形、平行四边形,判断结果输出true/false,结果之间以一个英文空格符分隔。2:输入四个点坐标,判断是否是菱形、矩形、正方形,判断结果输出true/false,结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形,输出"not a quadrilateral"
3:输入四个点坐标,判断是凹四边形(false)还是凸四边形(true),输出四边形周长、面积,结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形,输出"not a quadrilateral"
4:输入六个点坐标,前两个点构成一条直线,后四个点构成一个四边形或三角形,输出直线与四边形(也可能是三角形)相交的交点数量。如果交点有两个,再按面积从小到大输出四边形(或三角形)被直线分割成两部分的面积(不换行)。若直线与四边形或三角形的一条边线重合,输出"The line is coincide with one of the lines"。若后四个点不符合四边形或三角形的输入,输出"not a quadrilateral or triangle"。
后四个点构成三角形的情况:假设三角形一条边上两个端点分别是x、y,边线中间有一点z,另一顶点s:
1)符合要求的输入:顶点重复或者z与xy都相邻,如x x y s、x z y s、x y x s、s x y y。此时去除冗余点,保留一个x、一个y。
2) 不符合要求的输入:z 不与xy都相邻,如z x y s、x z s y、x s z y5:输入五个点坐标,输出第一个是否在后四个点所构成的四边形(限定为凸四边形,不考虑凹四边形)或三角形(判定方法见选项4)的内部(若是四边形输出in the quadrilateral/outof the quadrilateral,若是三角形输出in the triangle/outof the triangle)。如果点在多边形的某条边上,输出"on the triangle或者on the quadrilateral"。若后四个点不符合四边形或三角形,输出"not a quadrilateral or triangle"。
-
题目设计
首先,肯定是要利用之前已经构建好的三角形,点,线的类等,再构建一个四边形类
(此处不对switch语句的书写和之前已经做好的格式输入以及格式化输出作设计,因为之前已经写好或简单改写即可)
显然,四边形中需要存入四个点对象,我还存入了四条线对象,方便调用。(构造函数不细说)对于题目1:
①类中需要添加判断是否为四边形以及是否为平行四边形的方法
②显然判断平行四边形的方法中可以先判断其是否为四边形,再进行接下来的判断对于题目2:
①需要添判断是否为菱形、矩形、正方形的方法
②其中,菱形,矩形调用是否为平行四边形的方法,正方形可以调用是否为菱形和矩形即可对于题目3:
①添加判断凹四边形的方法(非凹即凸,因此不需要有判断凸四边形的方法)
②添加求周长,求面积的方法
③其中周长可以直接用遍历线求线长和,面积可以切成两个三角形,调用三角形方法求对于题目4:
①可以设计一个求线与四边形交点的方法(之前三角形中实现过,修改一下即可)
②通过交点在线上的位置求切割的面积(之前也在三角形中实现过,也需要修改一下)对于题目5:
①添加一个点是否在四边形内的方法以及点是否在四边形上的方法
②点在四边形内的方法因为限定为凸四边形,因此可以直接通过求各边到该点构成的三角形求面积,相等则在四边形上或内
③点在四边形上则可以遍历每一条边,求该点到边的距离,如果为0则显然在四边形上 -
完整代码
import java.util.ArrayList; import java.util.Scanner; public class Main { public static void main(String[] args) { Scanner input=new Scanner(System.in); String[] str=Input.split_input(input.nextLine()); String op_str=str[0],xy_str[]=Input.get_xy(str[1]); Format.trueInputLength(str); Format.trueOp(op_str); Format.trueXY(xy_str); Format.pointNum(xy_str, Input.getPointNum(op_str)); switch (op_str) { case "1": Quadrilateral q1=new Quadrilateral(xy_str[0],xy_str[1],xy_str[2],xy_str[3]); Format.quest1(q1); break; case "2": Quadrilateral q2=new Quadrilateral(xy_str[0],xy_str[1],xy_str[2],xy_str[3]); Format.quest2(q2); break; case "3": Quadrilateral q3=new Quadrilateral(xy_str[0],xy_str[1],xy_str[2],xy_str[3]); Format.quest3(q3); break; case "4": Line l4=new Line(xy_str[0],xy_str[1]); Quadrilateral q4=new Quadrilateral(xy_str[2],xy_str[3],xy_str[4],xy_str[5]); Format.quest4(l4,q4); break; case "5": Point p5=new Point(xy_str[0]); Quadrilateral q5=new Quadrilateral(xy_str[1],xy_str[2],xy_str[3],xy_str[4]); Format.quest5(p5,q5); break; default: System.out.println("Wrong Format"); break; } } } class Input{ /* 从用户的输入中获取坐标 * 输入:s为一个只含坐标的字符串 * 输出:String类型的坐标数组(按空格划分,所以坐标可能正确,判断格式正确与否放在Format类里) * */ public static String[] get_xy(String s) { //s为坐标 return s.split(" "); } /* 从用户的输入中分离坐标和选项 * 输入:s为一个选项+坐标的输入 * 输出:分离选项,坐标字符串 * */ public static String[] split_input(String s) {// String[] str=s.split(":",-1); return str; } public static int getPointNum(String op) { if(op.equals("4")) return 6; else if(op.equals("5")) return 5; return 4; } } class Format{ public static void trueOp(String s) { if(s.matches("[1-5]")) return; System.out.print("Wrong Format"); System.exit(0); } /* 判断坐标数组s中每个值是否合法 * 输入:坐标数组s * 输出:每个值都合法输出true,有一个不合法则输出false * */ public static void trueXY(String[] s) { for(int i=0;i<s.length;i++) { if(!trueXY(s[i])) { System.out.println("Wrong Format"); System.exit(0); } } } //判断坐标s是否合法 public static boolean trueXY(String s) { if(s.split(",").length!=2) return false; else if(s.matches("^([+-])?([1-9][0-9]*|[0])(\\.[0-9]+)?,([+-])?([1-9][0-9]*|[0])(\\.[0-9]+)?$"))//判断是否为合法坐标的一个正则表达式 return true; return false; } // 格式化字符串 public static double Format_Str(double s,int num) { String s1=String.format("%."+num+"f",s);//保留num位 s=Double.parseDouble(s1); return s; } public static void trueInputLength(String[] str){ if(str.length==2) return; System.out.print("Wrong Format"); System.exit(0); } public static void pointNum(String[] s,int num) { if(s.length!=num) { System.out.println("wrong number of points"); //System.out.println(num+"wrong number of points"); System.exit(0); } } public static ArrayList<Point> deleteCoinPoint(Point[] p) { ArrayList<Point> p1=new ArrayList<Point>(); for(int i=0;i<p.length;i++) { if(!p[i].Equel(p1)) p1.add(p[i]); } return p1; } public static void quest1(Quadrilateral q) { if(q.pointCoincide()) System.out.print("points coincide"); else if(q.isParallelogram()) System.out.print("true true"); else if(q.isQuadrilateral()) System.out.print("true false"); else System.out.print("false false"); } public static void quest2(Quadrilateral q) { if(q.pointCoincide()) System.out.print("points coincide"); else if(!q.isQuadrilateral()) System.out.print("not a quadrilateral");// System.out.print("not a quadrilatera"); else if(q.isSquare()) System.out.print("true true true"); else if(q.isRectangle()) System.out.print("false true false"); else if(q.isDiamond()) System.out.print("true false false"); else System.out.print("false false false"); } public static void quest3(Quadrilateral q) { if(q.pointCoincide()) System.out.print("points coincide"); else if(!q.isQuadrilateral()) System.out.print("not a quadrilateral");// System.out.print("not a quadrilatera"); else{ System.out.print(q.isConvex()+" "); System.out.print(Format.Format_Str(q.getPerimeter(),3)+" "); System.out.print(Format.Format_Str(q.getArea(),3)); } } public static void quest4(Line l,Quadrilateral q) { if(l.Point_Cioncide()) System.out.println("points coincide"); else if(!q.isQuadrilateral()&&!q.isTriangle()) System.out.println("not a quadrilateral or triangle"); else if(l.lineCoincide(q.l)) System.out.println("The line is coincide with one of the lines"); else { ArrayList<Point> p=Format.deleteCoinPoint(q.p);; if(q.isTriangle()&&p.size()==3){ Triangle t=new Triangle(p.get(0),p.get(1),p.get(2)); p=q.lineCrossPoint(l); System.out.print(p.size()); if(p.size()==2) { double area=t.lineCrossArea(p.get(0),p.get(1)); area=Math.min(area,t.getArea()-area); System.out.print(" "+Format.Format_Str(area, 3)+" "+Format.Format_Str(t.getArea()-area,3)); } } else { p=q.lineCrossPoint(l); System.out.print(p.size()); if(p.size()==2) { double area=q.lineCrossArea(p.get(0),p.get(1)); area=Math.min(area,q.getArea()-area); System.out.print(" "+Format.Format_Str(area, 3)+" "+Format.Format_Str(q.getArea()-area,3)); } } } } public static void quest5(Point p,Quadrilateral q) { String s=null; if(q.isQuadrilateral()) s="quadrilateral"; else if(q.isTriangle()) s="triangle"; else { System.out.println("not a quadrilateral or triangle"); System.exit(0); } if(q.pointOnQuad(p)) System.out.print("on the "+s); else if(q.pointInside(p)) System.out.print("in the "+s); else System.out.print("outof the "+s); } } class Point{ double x,y; public Point(String a) {//传入参数为"x,y"这类的字符串 String[] s=a.split(","); this.Set_x(Double.parseDouble(s[0])); this.Set_y(Double.parseDouble(s[1])); } public Point(double x,double y) { this.Set_x(x); this.Set_y(y); } //求两点之间距离 public double get_dis(Point a){ return Math.sqrt(Math.pow((this.x-a.x),2)+Math.pow((this.y-a.y),2)); } /* 判断本身与其他的点是否相等 * 输入:点列表a * 输出:如果点列表a中有与本身坐标相同的点则返回true,否则false * */ public boolean Equel(ArrayList<Point> a) { for(int i=0;i<a.size();i++) { if(this.Equel(a.get(i))) return true; } return false; } //判断两点坐标是否相等 public boolean Equel(Point a) { if(Math.abs(this.x-a.x)<0.000001&&Math.abs(this.y-a.y)<0.000001) return true; return false; } //设置自身的x坐标 public void Set_x(double x) { this.x=x; } //设置自身的y坐标 public void Set_y(double y) { this.y=y; } } class Line{ Point p1,p2; Double A,B,C; /* 构造函数 * 输入:线的两个点a,b * 输出: * */ public Line(Point a,Point b) { this.Set_p1(a); this.Set_p2(b); this.getABC(); } public Line(String s1,String s2) { Point p1=new Point(s1); Point p2=new Point(s2); this.Set_p1(p1); this.Set_p2(p2); this.getABC(); } //设置线的构造点 public void Set_p1(Point a){ this.p1=a; } public void Set_p2(Point a) { this.p2=a; } //计算直线一般式方程的ABC public void getABC() { this.A=p2.y-p1.y; this.B=p1.x-p2.x; this.C=p2.x*p1.y-p1.x*p2.y; } /* 计算点到线的距离 * 输入:点a * 输出:点a到自身的距离 * */ public double P_to_L_dis(Point a) { if(this.Point_Cioncide()) return 0; double dis=Math.abs(this.A*a.x+this.B*a.y+this.C)/Math.sqrt(Math.pow(this.A,2)+Math.pow(this.B,2)); return dis; } public double getNumber(Point p) { if(Math.abs(this.A*p.x+this.B*p.y+this.C)<0.000001) return 0; return this.A*p.x+this.B*p.y+this.C; } /* 计算线的长度 * 输入: * 输出:自身的长度 * */ public double getLength() { return this.p1.get_dis(this.p2); } /* 计算线的长度是否相等 * 输入:线l * 输出:两线是否相等 * */ public boolean lengthEquel(Line l) { if(Math.abs(this.getLength()-l.getLength())<0.000001) return true; return false; } /* 判断两线是否平行 * 输入:线l2 * 输出:两线平行则输出true,否则输出false * */ public boolean lineParallel(Line l2) { if((Math.abs(this.A*l2.B-this.B*l2.A)<0.000001&&Math.abs(this.A*l2.C-this.C*l2.A)>0.000001) ||(Math.abs(this.A-l2.A)<0.000001&&Math.abs(this.A)<0.000001)) return true; return false; } //逐个判断线与l数组内的每个线是否重合 public boolean lineCoincide(Line[] l) { for(int i=0;i<l.length;i++) { if(!l[i].Point_Cioncide()&&this.lineCoincide(l[i])) return true; } return false; } /* 判断两线是否重合 * 输入:线l2 * 输出:两线重合则输出true,否则输出false * */ public boolean lineCoincide(Line l2) { if(Math.abs(this.A*l2.B-this.B*l2.A)<0.000001 &&Math.abs(this.A*l2.C-this.C*l2.A)<0.000001 &&Math.abs(this.B*l2.C-this.C*l2.B)<0.000001) return true; return false; } /* 判断线的两点是否重合 * 输入: * 输出:两点重合则输出true,否则输出false * */ public boolean Point_Cioncide() { if(this.p1.Equel(this.p2)) return true; return false; } /* 求两线交点 * 输入:线l2 * 输出:交点 * */ public Point getCrossPoint(Line l2) { double Y=(this.C*l2.A-l2.C*this.A)/(this.A*l2.B-l2.A*this.B); double X=(l2.C*this.B-this.C*l2.B)/(this.A*l2.B-l2.A*this.B); Point p=new Point(X,Y); return p; } /* 求点是否在线内(即在线段内) * 输入:点a * 输出:点在线段内则输出true,否则输出false * */ public boolean pointOnLine(Point a) { if(!this.Point_Cioncide()&&a.get_dis(this.p1)+a.get_dis(this.p2)-this.getLength()<0.00000001) return true; return false; } } class Triangle{ Line l1,l2,l3; /* 构造方法 * 输入:线l1,l2,l3 * 输出: * */ public Triangle(Line l1,Line l2,Line l3) { this.l1=l1; this.l2=l2; this.l3=l3; } /* 构造方法 * 输入:点p1,p2,p3 * 输出: * */ public Triangle(Point p1,Point p2,Point p3) { this.l1=new Line(p1,p2); this.l2=new Line(p1,p3); this.l3=new Line(p2,p3); } /* 构造方法 * 输入:三个点的坐标 * 输出: * */ public Triangle(double x1,double y1,double x2,double y2,double x3,double y3) { this.l1=new Line(new Point(x1,y1),new Point(x2,y2)); this.l2=new Line(new Point(x1,y1),new Point(x3,y3)); this.l3=new Line(new Point(x2,y2),new Point(x3,y3)); } /* 求三角形的面积 * 输入: * 输出:三角形的面积 * */ public double getArea() { return this.l3.P_to_L_dis(this.l1.p1)*this.l3.getLength()/2; } /* 求线l与三角形交点数量 * 输入:线l * 输出:线与三角形的交点列表(重复点已去除) * */ public ArrayList<Point> lineCrossPoint(Line l) { ArrayList<Point> p = new ArrayList<Point>(); Point crossp1=this.l1.getCrossPoint(l); Point crossp2=this.l2.getCrossPoint(l); Point crossp3=this.l3.getCrossPoint(l); if(this.l1.pointOnLine(crossp1)&&!crossp1.Equel(p)) p.add(crossp1); if(this.l2.pointOnLine(crossp2)&&!crossp2.Equel(p)) p.add(crossp2); if(this.l3.pointOnLine(crossp3)&&!crossp3.Equel(p)) p.add(crossp3); return p; } public double lineCrossArea(Point p1, Point p2) { Point p3=null; if(this.l1.pointOnLine(p1)&&this.l2.pointOnLine(p2)) p3=this.l1.p1; else if(this.l1.pointOnLine(p1)&&this.l3.pointOnLine(p2)) p3=this.l1.p2; else if(this.l2.pointOnLine(p1)&&this.l3.pointOnLine(p2)) p3=this.l2.p2; Triangle t=new Triangle(p3,p1,p2); return t.getArea(); } /* 判断三角形的三点是否为正确的三角形 * 输入: * 输出:能构成三角形则输出true,否则输出false; * */ public boolean isTriangle() { if(this.l1.getLength()+this.l2.getLength()-this.l3.getLength()>0.000001) return true; return false; } } class Quadrilateral { Point[] p=new Point[4]; Line[] l=new Line[4]; Quadrilateral(String s0,String s1,String s2,String s3) { Point p0=new Point(s0); Point p1=new Point(s1); Point p2=new Point(s2); Point p3=new Point(s3); this.initQuad(p0, p1, p2, p3); } Quadrilateral(Point p0,Point p1,Point p2,Point p3) { this.initQuad(p0, p1, p2, p3); } public void initQuad(Point p0,Point p1,Point p2,Point p3) { p[0]=p0;p[1]=p1;p[2]=p2;p[3]=p3; l[0]=new Line(p[0],p[1]); l[1]=new Line(p[1],p[2]); l[2]=new Line(p[2],p[3]); l[3]=new Line(p[3],p[0]); } public boolean pointCoincide() { int i,j; for(i=0;i<p.length;i++) { j=(i+1)%p.length; if(p[i].Equel(p[j])) return true; } return false; } public boolean hasEuqalPoint() { int i,j; for(i=0;i<p.length-1;i++) { for(j=i+1;j<p.length;j++) if(p[i].Equel(p[j])) return true; } return false; } public boolean isQuadrilateral() { int i; if(this.pointCoincide()) return false; for(i=0;i<l.length;i++) { if(l[i].lineCoincide(l[(i+1)%l.length])) return false; } Point cross1=l[2].getCrossPoint(l[0]); Point cross2=l[3].getCrossPoint(l[1]); if((l[2].pointOnLine(cross1)&&l[0].pointOnLine(cross1))|| (l[3].pointOnLine(cross2)&&l[1].pointOnLine(cross2))) return false; return true; } public boolean isTriangle() { ArrayList<Point> p=new ArrayList<Point>(); if(this.hasEuqalPoint()) p=Format.deleteCoinPoint(this.p); else for(int i=0;i<this.p.length;i++) p.add(this.p[i]); //ArrayList<Point> p=Format.deleteCoinPoint(this.p); switch (p.size()) { case 3:{ Triangle t=new Triangle(p.get(0),p.get(1),p.get(2)); if(t.isTriangle()) return true; return false; } case 4:{ int i,j; for(i=0;i<this.l.length;i++) { j=(i+1)%this.l.length; if(l[i].lineCoincide(l[j])) { Line line=new Line(this.p[i],this.p[(j+1)%this.l.length]);//Line line=new Line(this.p[i],this.p[j+1]); if(Math.abs(line.getLength()-(l[i].getLength()+l[j].getLength()))<0.000001) return true; } } return false; } default: return false; } } public boolean isParallelogram() { if(this.isQuadrilateral()) { if(this.l[0].lineParallel(this.l[2])&&this.l[1].lineParallel(this.l[3])) return true; } return false; } public boolean isDiamond() { if(this.isParallelogram()&&this.l[0].lengthEquel(this.l[1])) return true; return false; } public boolean isRectangle() { if(this.isParallelogram()) { double a=this.p[0].get_dis(this.p[1]); double b=this.p[1].get_dis(this.p[2]); double c=this.p[2].get_dis(this.p[0]); if(Math.abs(a*a+b*b-c*c)<0.000001) return true; } return false; } public boolean isSquare() { if(this.isDiamond()&&this.isRectangle()) return true; return false; } public boolean isConvex() { double area1=new Triangle(p[0],p[1],p[2]).getArea(); double area2=new Triangle(p[2],p[3],p[1]).getArea(); double area3=new Triangle(p[1],p[2],p[3]).getArea(); double area4=new Triangle(p[3],p[0],p[1]).getArea(); if(Math.abs(area1+area2-area3-area4)<0.000001) return true; return false; } public double getPerimeter() { double sum=0; for(int i=0;i<this.l.length;i++) { sum+=l[i].getLength(); } return sum; } public double getArea() { int tar; Line line=new Line(this.p[0],this.p[2]); if(line.getNumber(this.p[1])*line.getNumber(this.p[3])<0) tar=1; else tar=-1; double h1=line.P_to_L_dis(p[1]); double h3=line.P_to_L_dis(p[3]); double len=line.getLength(); return Math.abs(len*h1/2+tar*len*h3/2); } public Triangle getTriangle() { ArrayList<Point> p=Format.deleteCoinPoint(this.p); return new Triangle(p.get(0),p.get(1),p.get(2)); } public ArrayList<Point> lineCrossPoint(Line l) { ArrayList<Point> p = new ArrayList<Point>(); Point crossp1=this.l[0].getCrossPoint(l); Point crossp2=this.l[1].getCrossPoint(l); Point crossp3=this.l[2].getCrossPoint(l); Point crossp4=this.l[3].getCrossPoint(l); if(this.l[0].pointOnLine(crossp1)&&!crossp1.Equel(p)) p.add(crossp1); if(this.l[1].pointOnLine(crossp2)&&!crossp2.Equel(p)) p.add(crossp2); if(this.l[2].pointOnLine(crossp3)&&!crossp3.Equel(p)) p.add(crossp3); if(this.l[3].pointOnLine(crossp4)&&!crossp4.Equel(p)) p.add(crossp4); return p; } public double lineCrossArea(Point p1,Point p2) { double area=0; if(this.l[0].pointOnLine(p1)&&this.l[1].pointOnLine(p2)) area=new Triangle(p[1],p1,p2).getArea(); else if(this.l[0].pointOnLine(p1)&&this.l[2].pointOnLine(p2)) { Quadrilateral q=new Quadrilateral(p1,this.p[1],this.p[2],p2); area=q.getArea(); } else if(this.l[0].pointOnLine(p1)&&this.l[3].pointOnLine(p2)) area=new Triangle(p[0],p1,p2).getArea(); else if(this.l[1].pointOnLine(p1)&&this.l[2].pointOnLine(p2)) area=new Triangle(p[2],p1,p2).getArea(); else if(this.l[1].pointOnLine(p1)&&this.l[3].pointOnLine(p2)){ Quadrilateral q=new Quadrilateral(p1,p2,this.p[3],this.p[2]); area=q.getArea(); } else if(this.l[2].pointOnLine(p1)&&this.l[3].pointOnLine(p2)) area=new Triangle(p[3],p1,p2).getArea(); return area; } public boolean pointOnQuad(Point p) { for(int i=0;i<this.l.length;i++) { if(this.l[i].pointOnLine(p)) return true; } return false; } public boolean pointInside(Point p) { double area; double len0=this.l[0].getLength(),len1=this.l[1].getLength(), len2=this.l[2].getLength(),len3=this.l[3].getLength(); double h0=this.l[0].P_to_L_dis(p),h1=this.l[1].P_to_L_dis(p), h2=this.l[2].P_to_L_dis(p),h3=this.l[3].P_to_L_dis(p); double sumarea=(len0*h0+len1*h1+len2*h2+len3*h3)/2; area=this.getArea();//case48:5:3,1 0,0 3,0 5,3 0,0 if(Math.abs(sumarea-area)<0.000001) return true; return false; } } -
SourceMonitor分析
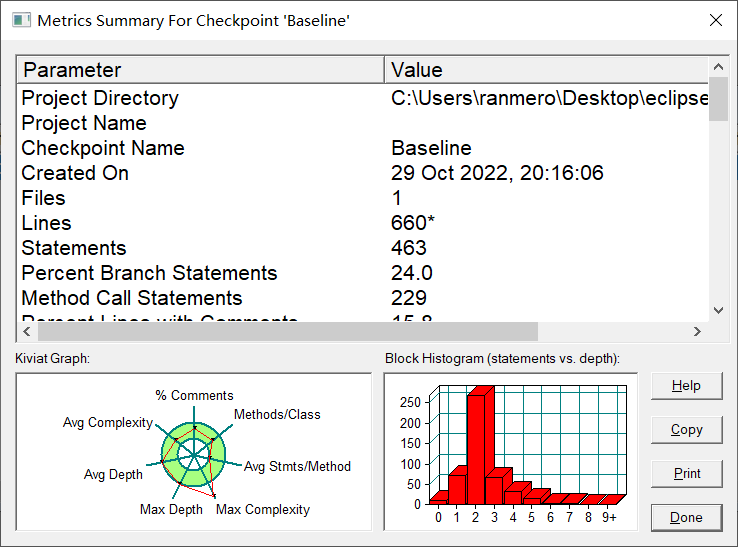
Kiviat Graph分析
①注释分析:注释数量还算适中
②每个类中方法数分析:每个类中的方法也比较合适,在绿圈中间位置
③每个方法中有效代码行数分析:每个方法中有效行数虽然在绿圈中,但行数较少,可能是方法细分的太详细了
④最大圈复杂度分析:最大圈复杂度比较高,可能原因还是连续的if else
⑤最大深度分析:最大深度已经到临界点了,还需要再优化
⑥平均深度分析:平均深度也比较高,因此可以略微减少嵌套调用
⑦平均圈复杂度分析:平均圈复杂度还是比较好的,保持在适中水平Block Histogram分析
显然可以看出,深度的主要集中在2,即便最大深度比较高,但也只是个例
总得来说还是处于较低位置
PTA题目集5——两题写一起(本来就是一道题,太长分成了两道给我们写而已)
-
题目内容
用户输入一组选项和数据,进行与五边形有关的计算。
以下五边形顶点的坐标要求按顺序依次输入,连续输入的两个顶点是相邻顶点,第一个和最后一个输入的顶点相邻。
选项包括:1:输入五个点坐标,判断是否是五边形,判断结果输出true/false。
2:输入五个点坐标,判断是凹五边形(false)还是凸五边形(true),如果是凸五边形,则再输出五边形周长、面积,结果之间以一个英文空格符分隔。 若五个点坐标无法构成五边形,输出"not a pentagon"
3:输入七个点坐标,前两个点构成一条直线,后五个点构成一个凸五边形、凸四边形或凸三角形,输出直线与五边形、四边形或三角形相交的交点数量。如果交点有两个,再按面积从小到大输出被直线分割成两部分的面积(不换行)。若直线与多边形形的一条边线重合,输出"The line is coincide with one of the lines"。若后五个点不符合五边形输入,若前两点重合,输出"points coincide"。
4:输入十个点坐标,前、后五个点分别构成一个凸多边形(三角形、四边形、五边形),判断它们两个之间是否存在包含关系(一个多边形有一条或多条边与另一个多边形重合,其他部分都包含在另一个多边形内部,也算包含)。
两者存在六种关系:1、分离(完全无重合点) 2、连接(只有一个点或一条边重合) 3、完全重合 4、被包含(前一个多边形在后一个多边形的内部)5、交错 6、包含(后一个多边形在前一个多边形的内部)。
各种关系的输出格式如下:
1、no overlapping area between the previous triangle/quadrilateral/ pentagon and the following triangle/quadrilateral/ pentagon
2、the previous triangle/quadrilateral/ pentagon is connected to the following triangle/quadrilateral/ pentagon
3、the previous triangle/quadrilateral/ pentagon coincides with the following triangle/quadrilateral/ pentagon
4、the previous triangle/quadrilateral/ pentagon is inside the following triangle/quadrilateral/ pentagon
5、the previous triangle/quadrilateral/ pentagon is interlaced with the following triangle/quadrilateral/ pentagon
6、the previous triangle/quadrilateral/ pentagon contains the following triangle/quadrilateral/ pentagon5:输入十个点坐标,前、后五个点分别构成一个凸多边形(三角形、四边形、五边形),输出两个多边形公共区域的面积。注:只考虑每个多边形被另一个多边形分割成最多两个部分的情况,不考虑一个多边形将另一个分割成超过两个区域的情况。
6:输入六个点坐标,输出第一个是否在后五个点所构成的多边形(限定为凸多边形,不考虑凹多边形),的内部(若是五边形输出in the pentagon/outof the pentagon,若是四边形输出in the quadrilateral/outof the quadrilateral,若是三角形输出in the triangle/outof the triangle)。输入入错存在冗余点要排除,冗余点的判定方法见选项5。如果点在多边形的某条边上,输出"on the triangle/on the quadrilateral/on the pentagon"。
-
题目设计
这一题可以向PTA4一样,构建一个五边形类,然后浏览题目设计五边形中的每一个方法,思考实现
但是,我认为这样还是过于麻烦,原因是如果到时候加入六边形,七边形等等
免不了又添加一堆诸如求面积,求周长等方法,实在难看
因此,我重构了代码,构建一个多边形类,将三角形,四边形,五边形,甚至之后六边形等,都可以继承多边形类
在多边形类中实现求面积,求周长,判断凹凸,判断能否构成多边形等
再构建多边形类后,依照题目思考哪些方法该放在多边形中,哪些方法该放在具体的多边形中(即三角形,四边形等具体多边形)对于题目1:
①多边形类中只需要添加一个判断是否为多边形的方法即可
②要判断是否是五边形,首先得判断其是一个多边形,同时,如果它还有5个点(或者5条边)则是五边形对于题目2:
①可以在多边形类中添加一个判断是否为凹多边形的方法即可
②也可以在多边形中添加一个凹凸的布尔类型的值用于区分凹凸四边形
③取巧方法:判断凹凸性和判断是否能构成多边形的条件几乎一样,只需要将决定条件中的&&改为||即可(具体见代码)对于题目3:
①在多边形类中添加直线穿过多边形求交点的方法(可以参考之前的直线穿过四边形求交点的方法,略微修改即可)
②在多边形类中添加求直线穿过多边形求切割面积的方法(同理可以参考,略微修改即可)
③显然,因为设置了多边形,因此创建时后五个点无需判断其是几边形,直接调用方法即可,大大节省了代码对于题目4:
①小tip:通过分析发现写这题之前先写题目5和题目6,再写这题可以轻松很多,下面的分析也是依照写了题5和题6进行的
②多边形中添加判断两多边形是否分离的方法:
对于一个多边形,如果其点全在另一个多边形外(可以复用题目6中方法),同时两多边形相交面积为0(复用题目5中的方法),则两多边形分离③多边形中添加判断两多边形是否连接的方法:
对于一个多边形,如果其只有一个点或一条边在另一个多边形上(也可以复用题目6中方法),同时两多边形相交面积为0(复用题目5中的方法),则两多边形连接④多边形中添加判断两多边形是否完全重合的方法:
对于一个多边形,如果其边全与另一个多边形重合,则两多边形重合⑤多边形中添加判断前一个多边形是否被后一个多边形包含的方法:
如果两多边形相交面积(复用题5)与前一个多边形面积相等且前一个多边形点全在后一个多边形内⑥多边形中添加判断两多边形是否交错的方法:
如果两多边形相交面积(复用题5)面积与两个多边形中任何一个都不相等且不为0则交错⑦不需要添加后一个是否被前一个包含,调用时反正来就行
对于题目5:
①多边形中添加一个两多边形求交点的方法:
即对一个多边形的每一条边都当作一条直线去切割另一个多边形,交点添加到列表
(若该切割直线的起点在多边形内,先添加仅列表中)(记得去重)②多边形中添加一个求两多边形求相交面积的方法:
其得到两多边形的交点,并构造成新的多边形,然后求面积即可③小Tip:求交点先用面积小的多边形去切面积大的,然后再用面积大的切面积小的,合起来去重才能过
对于题目6:
①类中添加一个点是否在多边形上的方法:
显然可以参照之前的四边形,用面积法或者射线法都行 -
完整源码(其中多余的部分是在之后的题目中添加的,本题中用不到)
import java.util.Scanner; import java.util.ArrayList; public class Main { public static void main(String[] args) { Scanner input=new Scanner(System.in); String s=input.nextLine(); Format.trueFormat(s);//判断输入的s是否正确 String op=Input.getOp(s),xy[]=Input.getXY(s);//使用Input中的方法从s中提取Op和XY Format.truePointNumber(op,xy); ArrayList<Point> plist=Input.xyTurnList(xy);//将xy字符串数组转化为点列表 switch (op){ case "1": Question.question1(plist); break; case "2": Question.question2(plist); break; case "3": Question.question3(plist); break; case "4": Question.question4(plist); break; case "5": Question.question5(plist); break; case "6": Question.question6(plist); break; } } } class Question{ public static void question1(ArrayList<Point> plist){ Pentagon p=new Pentagon(plist); if(p.truePolygon()) System.out.println("true"); else System.out.println("false"); } public static void question2(ArrayList<Point> plist){ Pentagon p=new Pentagon(plist); if(!p.truePolygon()){ System.out.println("not a pentagon"); } else if(p.convexPentagon()){ double perimeter=Format.Format_Str(p.getPerimeter(),3); double area=Format.Format_Str(p.getArea(),3); System.out.println("true "+perimeter+" "+area); } else System.out.println("false"); } public static void question3(ArrayList<Point> plist){ Line line=new Line(plist.get(0),plist.get(1)); plist.remove(0); plist.remove(0); Polygon polygon=new Polygon(plist); if(line.pointCoincide()) System.out.println("points coincide"); else if(!polygon.truePolygon()) System.out.println("not a polygon"); else if(line.lineCoincide(polygon.llist)) System.out.println("The line is coincide with one of the lines"); else{ ArrayList<Point> crosslist=polygon.lineCrossPoint(line); System.out.print(crosslist.size()+" "); if(crosslist.size()==2){ double area= polygon.lineCrossArea(crosslist); double sumarea=polygon.getArea(); area=Math.min(area,sumarea-area); System.out.println(Format.Format_Str(area,3)+" "+Format.Format_Str(sumarea-area,3)); } } } public static void question4(ArrayList<Point> plist){ Polygon polygon1=new Polygon(Format.subArrayList(plist,0,5)); Polygon polygon2=new Polygon(Format.subArrayList(plist,5,10)); String[] shape=new String[]{"null","point","line","triangle","quadrilateral","pentagon"}; if(polygon1.noOverlapping(polygon2)) System.out.println("no overlapping area between the previous "+shape[polygon1.plist.size()]+" and the following "+shape[polygon2.plist.size()]); else if(polygon1.isConnect(polygon2)) System.out.println("the previous "+shape[polygon1.plist.size()]+" is connected to the following "+shape[polygon2.plist.size()]); else if(polygon1.coincideWith(polygon2)) System.out.println("the previous "+shape[polygon1.plist.size()]+" coincides with the following "+shape[polygon2.plist.size()]); else if(polygon2.isInside(polygon1)) System.out.println("the previous "+shape[polygon1.plist.size()]+" is inside the following "+shape[polygon2.plist.size()]); else if(polygon1.isInterlaced(polygon2)) System.out.println("the previous "+shape[polygon1.plist.size()]+" is interlaced with the following "+shape[polygon2.plist.size()]); else if(polygon1.isInside(polygon2)) System.out.println("the previous "+shape[polygon1.plist.size()]+" contains the following "+shape[polygon2.plist.size()]); } public static void question5(ArrayList<Point> plist){ Polygon polygon1=new Polygon(Format.subArrayList(plist,0,5)); Polygon polygon2=new Polygon(Format.subArrayList(plist,5,10)); double area=polygon1.polygonCrossArea(polygon2); System.out.println(Format.Format_Str(area,3)); } public static void question6(ArrayList<Point> plist){ Point p1=plist.get(0); Polygon polygon=new Polygon(Format.subArrayList(plist,1,6)); String[] shape=new String[]{"null","point","line","triangle","quadrilateral","pentagon"}; if(polygon.pointOnPolygon(p1)) System.out.println("on the "+shape[polygon.plist.size()]); else if(polygon.pointInPolygon(p1)) System.out.println("in the "+shape[polygon.plist.size()]); else System.out.println("outof the "+shape[polygon.plist.size()]); } } class Input{ public static String[] getXY(String s) { // String[] str=s.split(":"); return str[1].split(" "); } public static String getOp(String s) {// String[] str=s.split(":"); return str[0]; } public static ArrayList<Point> xyTurnList(String[] str){ ArrayList<Point> plist=new ArrayList<Point>(); for(int i=0;i<str.length;i++) plist.add(new Point(str[i])); return plist; } } class Format { public static void trueFormat(String s) { if(!s.matches("^[1-6]:((([+-]?((0|[1-9][0-9]*)(\\.[0-9]+)?)),([+-]?(0|[1-9][0-9]*)(\\.[0-9]+)?))\\s?)+")) { System.out.println("Wrong Format"); System.exit(0); } } public static void truePointNumber(String s,String[] str){ int num=0; switch (s){ case "1": case "2":num=5;break; case "3":num=7;break; case "4": case "5":num=10;break; case "6":num=6;break; } if(num!=str.length){ System.out.println("wrong number of points"); System.exit(0); } } public static double Format_Str(double s,int num) { String s1=String.format("%."+num+"f",s); s=Double.parseDouble(s1); return s; } public static ArrayList<Point> subArrayList(ArrayList<Point> plist,int min,int max){ ArrayList<Point> newplist=new ArrayList<Point>(); for(Point point:plist.subList(min,max)) newplist.add(point); return newplist; } } class Polygon{ ArrayList<Point> plist=new ArrayList<Point>(); ArrayList<Line> llist=new ArrayList<Line>(); boolean convex; //多边形构造函数 Polygon(ArrayList<Point> plist){ this.deleteExtraPoint(plist); this.initPolygon(plist); } public void initPolygon(ArrayList<Point> plist) { int i,j; this.convex=true; for(i=0;i<this.plist.size();i++) { j=(i+1)%this.plist.size(); this.llist.add(new Line(this.plist.get(i),this.plist.get(j))); } } //求凸多边形的面积 public double getArea() { int i; double sum=0,len,h; for(Line line:llist) { len=line.getLength(); h=line.pointToLineDis(this.plist.get(0)); sum+=len*h/2; } return sum; } //求多边形周长 public double getPerimeter() { double sum=0; for(Line line :llist) sum+=line.getLength(); return sum; } public void deleteExtraPoint(ArrayList<Point> plist) { int i,j,k; for(i=0;i<plist.size();i++){ Point p=plist.get(i); if(!p.Equal(this.plist)) this.plist.add(p); } for(i=0;i<this.plist.size();){ j=(i+1)%this.plist.size(); k=(i+2)%this.plist.size(); Line l1=new Line(this.plist.get(i),this.plist.get(j)); if(l1.onExtendLine(this.plist.get(k))) this.plist.remove(j); else i++; } } public boolean truePolygon() { int i,j; for(i=0;i<this.llist.size();i++){ if(this.llist.get(i).lineCoincide(this.llist.get((i+1)%this.llist.size()))) return false; } for(i=0;i<this.llist.size();i++){ Line l1=this.llist.get(i); for(j=0;j<this.llist.size()-3;j++){ Line l2=this.llist.get((i+2+j)%this.llist.size()); Point cross=l1.getCrossPoint(l2); if(l1.pointOnLine(cross)&&l2.pointOnLine(cross)) return false; else if(l1.pointOnLine(cross)||l2.pointOnLine(cross)) this.convex=false; } } return true; } public ArrayList<Point> lineCrossPoint(Line crossline) { ArrayList<Point> crosslist=new ArrayList<Point>(); for(Line line:this.llist){ if(line.lineCoincide(crossline)){ crosslist.add(line.p1); crosslist.add(line.p2); } else{ Point cross=line.getCrossPoint(crossline); if(line.pointOnLine(cross)&&!cross.Equal(crosslist)){ crosslist.add(cross); } } } return crosslist; } public ArrayList<Point> segmentCrossPoint(Line crossline){ ArrayList<Point> crosslist=this.lineCrossPoint(crossline); for(int i=0;i<crosslist.size();){ if(!crossline.pointOnLine(crosslist.get(i))) crosslist.remove(crosslist.get(i)); else i++; } return crosslist; } public double lineCrossArea(ArrayList<Point> crosslist) { int i,min=-1,max=-1; Point cross1=crosslist.get(0),cross2=crosslist.get(1); Line line; for(i=0;i<this.llist.size();i++){ line=this.llist.get(i); if(line.pointOnLine(cross1)&&min==-1) min=i; if(line.pointOnLine(cross2)&&max==-1) max=i; } for(i=max;i>min;i--){ crosslist.add(this.plist.get(i)); } Polygon polygon=new Polygon(crosslist); return polygon.getArea(); } public int pointOutOfPolygonNum(Polygon polygon2) { int num=0; for(Point point:polygon2.plist){ if(this.pointOutOfPolygon(point)) num++; } return num; } public int pointOnPolygonNum(Polygon polygon2) { int num=0; for(Point point:polygon2.plist){ if(this.pointOnPolygon(point)) num++; } return num; } public int pointInPolygonNum(Polygon polygon2) { int num=0; for(Point point:polygon2.plist){ if(this.pointInPolygon(point)) num++; } return num; } public boolean noOverlapping(Polygon polygon2) { int num=this.pointOutOfPolygonNum(polygon2); double crossarea=this.polygonCrossArea(polygon2); if(Math.abs(crossarea)<0.000001&&num==polygon2.plist.size()) return true; return false; } public boolean isConnect(Polygon polygon2) { int num=this.pointOnPolygonNum(polygon2); double crossarea=this.polygonCrossArea(polygon2); if(Math.abs(crossarea)<0.000001&&(num==1||num==2)) return true; return false; } public boolean coincideWith(Polygon polygon2) { int num=this.pointOnPolygonNum(polygon2); double crossarea=this.polygonCrossArea(polygon2); if(Math.abs(crossarea-this.getArea())<0.000001&&num==polygon2.plist.size()) return true; return false; } public boolean isInside(Polygon polygon2) { int num=this.pointInPolygonNum(polygon2)+this.pointOnPolygonNum(polygon2); double crossarea=this.polygonCrossArea(polygon2); if(Math.abs(crossarea-polygon2.getArea())<0.000001&&num==polygon2.plist.size()) return true; return false; } public boolean isInterlaced(Polygon polygon2) { double crossarea=this.polygonCrossArea(polygon2); if(this.getArea()-crossarea>0.000001&&polygon2.getArea()-crossarea>0.000001) return true; return false; } public boolean pointOnPolygon(Point point) { for(Line line:this.llist){ if(line.pointOnLine(point)) return true; } return false; } public boolean pointOutOfPolygon(Point point) { double area=this.getArea(); double h,len,sum=0; for(Line line:this.llist){ len=line.getLength(); h=line.pointToLineDis(point); sum+=h*len/2; } if(sum-area>0.000001) return true; return false; } public boolean pointInPolygon(Point point1) { if(!this.pointOutOfPolygon(point1)&&!this.pointOnPolygon(point1)) return true; return false; } public ArrayList<Point> polygonCrossPoint(Polygon polygon1) { ArrayList<Point> crosslist=new ArrayList<Point>(); for(int i=0;i<polygon1.llist.size();i++){ Line line=polygon1.llist.get(i); if(this.pointInPolygon(line.p1)) crosslist.add(line.p1); crosslist.addAll(this.segmentCrossPoint(line)); } return crosslist; } public double polygonCrossArea(Polygon polygon2) { ArrayList<Point> crosslist1=this.polygonCrossPoint(polygon2); ArrayList<Point> crosslist2=polygon2.polygonCrossPoint(this); if(this.getArea()<polygon2.getArea()){ crosslist2.addAll(crosslist1); crosslist1=crosslist2; } else crosslist1.addAll(crosslist2); Polygon polygon3=new Polygon(crosslist1); return polygon3.getArea(); } } class Point{ double x,y; public Point(String a) {// String[] s=a.split(","); this.x=Double.parseDouble(s[0]); this.y=Double.parseDouble(s[1]); } public Point(double x,double y) { this.x=x; this.y=y; } public double get_dis(Point a){ return Math.sqrt(Math.pow((this.x-a.x),2)+Math.pow((this.y-a.y),2)); } public boolean Equal(ArrayList<Point> a) { for (Point point : a) { if (this.Equal(point)) return true; } return false; } public boolean Equal(Point a) { if(Math.abs(this.x-a.x)<0.000001&&Math.abs(this.y-a.y)<0.000001) return true; return false; } } class Line{ Point p1,p2; Double A,B,C; public Line(Point a,Point b) { this.p1=a; this.p2=b; this.getABC(); } public void getABC() { this.A=p2.y-p1.y; this.B=p1.x-p2.x; this.C=p2.x*p1.y-p1.x*p2.y; } public double pointToLineDis(Point a) { if(this.pointCoincide()) return 0; double dis=Math.abs(this.A*a.x+this.B*a.y+this.C)/Math.sqrt(Math.pow(this.A,2)+Math.pow(this.B,2)); return dis; } public double getNumber(Point p) { if(Math.abs(this.A*p.x+this.B*p.y+this.C)<0.000001) return 0; return this.A*p.x+this.B*p.y+this.C; } public double getLength() { return this.p1.get_dis(this.p2); } public boolean lineParallel(Line l2) { if((Math.abs(this.A*l2.B-this.B*l2.A)<0.000001&&Math.abs(this.A*l2.C-this.C*l2.A)>0.000001) ||(Math.abs(l2.A)<0.000001&&Math.abs(this.A)<0.000001)) return true; return false; } public boolean lineCoincide(ArrayList<Line> llist) { for(Line line:llist) { if(this.lineCoincide(line)) return true; } return false; } public boolean lineCoincide(Line l2) { if(Math.abs(this.A*l2.B-this.B*l2.A)<0.000001 &&Math.abs(this.A*l2.C-this.C*l2.A)<0.000001 &&Math.abs(this.B*l2.C-this.C*l2.B)<0.000001) return true; return false; } public boolean pointCoincide() { if(this.p1.Equal(this.p2)) return true; return false; } public Point getCrossPoint(Line l2) { double Y=(this.C*l2.A-l2.C*this.A)/(this.A*l2.B-l2.A*this.B); double X=(l2.C*this.B-this.C*l2.B)/(this.A*l2.B-l2.A*this.B); Point p=new Point(X,Y); return p; } public boolean pointOnLine(Point a) { if(!this.pointCoincide()&&a.get_dis(this.p1)+a.get_dis(this.p2)-this.getLength()<0.000001) return true; return false; } public boolean onExtendLine(Point p3){ Line l2=new Line(this.p2,p3); Line l3=new Line(this.p1,p3); if(this.lineCoincide(l2)&&Math.abs(l3.getLength()-this.getLength()-l2.getLength())<0.000001) return true; return false; } } class Triangle extends Polygon{ Triangle(ArrayList<Point> plist){ super(plist); } } class Quadrilateral extends Polygon{ Quadrilateral(ArrayList<Point> plist){ super(plist); } } class Pentagon extends Polygon{ Pentagon(ArrayList<Point> plist){ super(plist); } public boolean truePolygon(){ if(super.truePolygon()&&this.llist.size()==5) return true; return false; } public boolean convexPentagon() { return this.convex; } } -
SourceMonitor分析
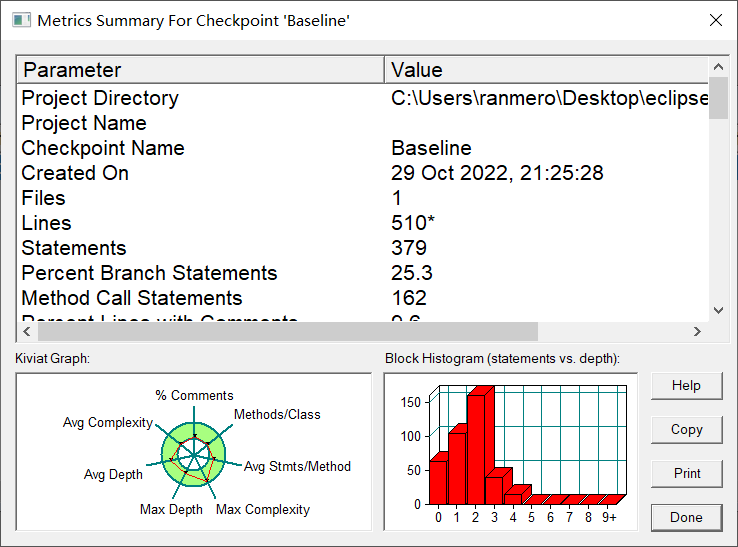
Kiviat Graph分析(全在绿圈目标达成!!!继承YYDS)
①注释分析:注释数量比较的少,后面好懒,不想写了
②每个类中方法数分析:每个类中的方法数也偏少,主要是三角形和四边形中都没有方法了,重构后几乎没东西了
③每个方法中有效代码行数分析:每个方法中的有效行数还是比较合适的
④最大圈复杂度分析:最大圈复杂度也恰到好处,可以接收,如果能在低一点就更好
⑤最大深度分析:最大深度比较合适,优秀~~~
⑥平均深度分析:平均深度也比较合适,优秀~~~
⑦平均圈复杂度分析:平均圈复杂度比较低(PS:低就低吧,就怕高了),说明代码比较简单Block Histogram分析
显然可以看出,深度的主要集中在0,1,2,这个分布就很nice,还得看我继承和多态
期中考试
-
题目内容
设计一个类表示平面直角坐标系上的点Point
设计一个类表示平面直角坐标系上的线Line
对题目中的点Point类和线Line类进行进一步抽象,定义一个两个类的共同父类Element(抽象类),将display()方法在该方法中进行声明(抽象方法),将Point类和Line类作为该类的子类。
再定义一个Element类的子类面Plane
在原有类设计的基础上,增加一个GeometryObject容器类
其余看图~~~
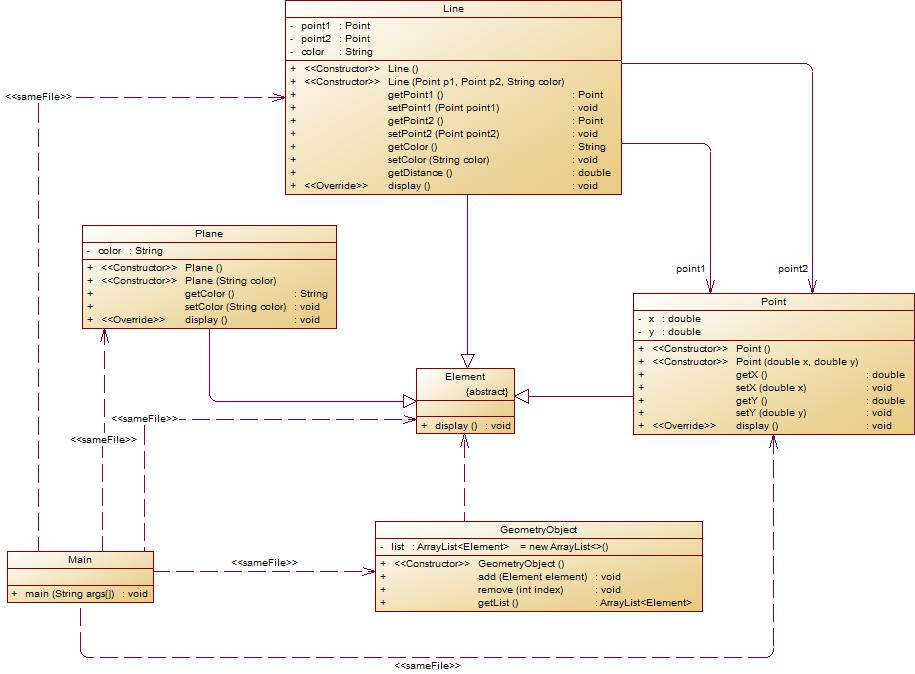
在主方法中,用户循环输入要进行的操作(choice∈[0,4]),其含义如下:
1:向容器中增加Point对象
2:向容器中增加Line对象
3:向容器中增加Plane对象
4:删除容器中第index - 1个数据,若index数据非法,则无视此操作
0:输入结束 -
题目设计
对于期中考试,老师已经给了类图,因此,类及其属性方法不需要我们设计
只要能读懂类图即可,即掌握好继承和多态的相关概念,因此,对于该题
并没有做过多的分析,跟着敲即可 -
完整源码(新增的,可以复用7-1中的Point类、Input类和Format类)
import java.util.ArrayList; import java.util.Scanner; public class Main { public static void main(String[] args){ Scanner input=new Scanner(System.in); GeometryObject elementList=new GeometryObject(); int choice; choice= input.nextInt(); while (choice!=0){ switch(choice) { case 1://insert Point object into list Point point=new Point(input.nextDouble(),input.nextDouble()); elementList.add(point); break; case 2://insert Line object into list Point point1=new Point(input.nextDouble(),input.nextDouble()); Point point2=new Point(input.nextDouble(),input.nextDouble()); Line line=new Line(point1,point2,input.next()); elementList.add(line); break; case 3://insert Plane object into list Plane plane=new Plane(input.next()); elementList.add(plane); break; case 4://delete index - 1 object from list elementList.remove(input.nextInt()-1); } choice= input.nextInt(); } for(Element element:elementList.getList()){ element.display(); } } } class GeometryObject { ArrayList<Element> list=new ArrayList<Element>(); GeometryObject(){ } public void add(Element element){ this.list.add(element); } public void remove(int index){ if(index<this.list.size()&&index>=0){ this.list.remove(index); } } public ArrayList<Element> getList(){ return this.list; } } abstract class Element{ public abstract void display(); } class Point extends Element{ private double x; private double y; Point(){ } Point(double x,double y){ if(x<=0||x>200||y<=0||y>200){ System.out.println("Wrong Format"); System.exit(0); } this.x=x; this.y=y; } public double getX() { return x; } public double getY() { return y; } public void setX(double x) { this.x = x; } public void setY(double y) { this.y = y; } public void display(){ System.out.println("("+String.format("%.2f",this.x)+","+String.format("%.2f",this.y)+")"); } public double getDis(Point a){ return Math.sqrt(Math.pow((this.x-a.x),2)+Math.pow((this.y-a.y),2)); } } class Line extends Element{ private Point point1; private Point point2; private String color; Line(){ } Line(Point point1,Point point2,String color){ this.point1=point1; this.point2=point2; this.color=color; } public Point getPoint1() { return point1; } public Point getPoint2() { return point2; } public String getColor() { return color; } public void setPoint1(Point point1) { this.point1 = point1; } public void setPoint2(Point point2) { this.point2 = point2; } public void setColor(String color) { this.color = color; } public double getDistance(){ return this.point1.getDis(this.point2); } public void display(){ System.out.println("The line's color is:"+this.color); System.out.println("The line's begin point's Coordinate is:"); this.point1.display(); System.out.println("The line's end point's Coordinate is:"); this.point2.display(); System.out.println("The line's length is:"+String.format("%.2f",this.getDistance())); } } class Plane extends Element{ String color; Plane(){ } Plane(String color){ this.color=color; } public String getColor() { return color; } public void setColor(String color) { this.color = color; } @Override public void display() { System.out.println("The Plane's color is:"+this.color); } } -
SourceMonitor分析
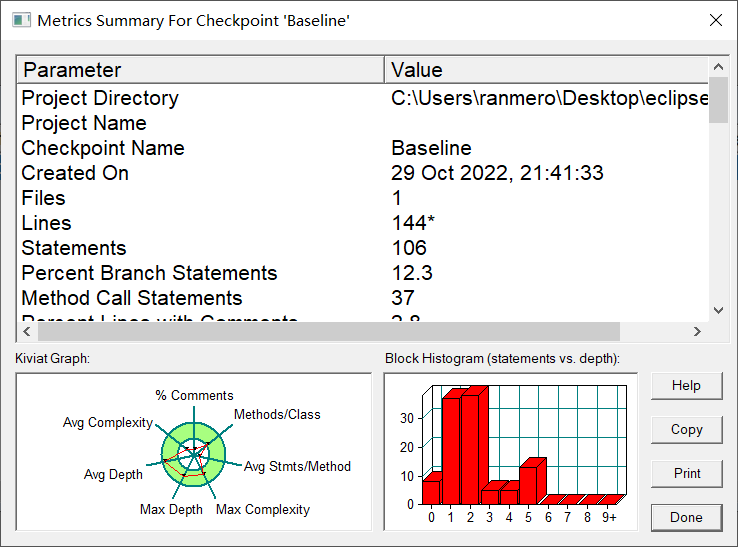
Kiviat Graph分析
①注释分析:没写注释.jpg,考试写完直接走!
②每个类中方法数分析:每个类中的方法数也偏少
③每个方法中有效代码行数分析:每个方法中行数很少,过于简单(题目也不允许方法复杂到那去)
④最大圈复杂度分析:最大圈复杂度还好,因为switch语句写在main里,虽然大部分时候不能这样,会导致圈复杂度过高
⑤最大深度分析:最大深度比较合适,多半也是因为switch语句在main里
⑥平均深度分析:平均深度还可以接收
⑦平均圈复杂度分析:平均复杂度很低,因为整个流程是线性的,除开switch语句几乎没分支Block Histogram分析
显然可以看出,深度的主要集中在1,2,也有一小截在5(很可能是switch导致的,从这里就可以看出switch语句在main函数的不好了)
三、踩坑心得
-
正则表达式
正则表达式书写不规范,提交了好多次都没过,后面还是查阅时才知道正则表达式中匹配.要用//.而之前
一直直接用.但是能过,以为没问题,然后就被卡住了下面时PTA4卡我的这个点

-
四个点构成三角形求面积
这两个点卡了我很久,卡到最后我甚至都测出35是什么了。原因是我没偷懒(我有罪),将四边形组成三角形求面积
的方法和四边形求面积的方法一起用,然后就yue了。最后构成一个三角形就过了下面时PTA4卡我的这个点

-
其余倒是没什么,PTA5总共就交了几次,还好没怎么卡住,不然真的遭罪
不过提交的时候这个没过,后面发现是去重的问题,解决的还蛮快的
四、改进意见
-
可以将之前PTA3,PTA4中三角形,四边形用到的所用方法进行提取,封装到现有
的架构里去,这样,多边形题目算是非常完善的over了 -
还是老问题,代码没有私有化(真的懒)
五、总结
通过这几次的实验,我只能说一定要用继承和多态!!
虽然我已经这样改了,但是还是希望大伙能重构一遍代码,代码复用真的很舒服
当然不仅仅是代码少,还有后面添加真的很方便,还是那个例子:
如果加入六边形,我判断是否为六边形的方法只需要调用父类中是否为多边形的方法,加上判断其是否有6个点即可
七边形,八边形同理!从这里也可以看出java类的强大之处了。
这几次作业算是很明显的培养了我对继承和多态的理解PTA4还在叠代码,PTA5直接利用继承和多态重构,期中测试
又复习一遍,个人认为收获很大


 浙公网安备 33010602011771号
浙公网安备 33010602011771号