695. [DFS]岛屿的最大面积

463. 岛屿的周长

岛屿问题是一类经典的网格搜索类问题。类似的岛屿题目还有：

• 200. 岛屿数量
• 463. 岛屿的周长
• 695. 岛屿最大面积

方法一：\(O(n^2)遍历搜索\)

只有一个岛屿，并且没有岛内湖，所以确定了所有的1都是相连的。

并且不会存在同一条边对应两个以上的位置，只要找到岛屿边界的1并计数周围的边即可。

遍历的是数组，边界也是有边的，所以只要周围是0，或者到达了数组边界，就会找到边。

// 执行耗时:8 ms,击败了75.57% 的Java用户
// 内存消耗:40.1 MB,击败了13.50% 的Java用户

class Solution {
    public int islandPerimeter(int[][] grid) {
        int res = 0;
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[0].length; j++) {
                if (grid[i][j] == 1) {
                    if (i == 0 || grid[i - 1][j] == 0) res++;
                    if (i == grid.length - 1 || grid[i + 1][j] == 0) res++;
                    if (j == 0 || grid[i][j - 1] == 0) res++;
                    if (j == grid[0].length - 1 || grid[i][j + 1] == 0) res++;
                }
            }
        }
        return res;
    }
}

方法二：DFS深度优先搜索

求岛屿的周长其实有很多种方法，如果用 DFS 遍历来求的话，有一种很简单的思路：岛屿的周长就是岛屿方格和非岛屿方格相邻的边的数量。

注意，这里的非岛屿方格，既包括水域方格，也包括网格的边界。我们可以画一张图，看得更清晰：

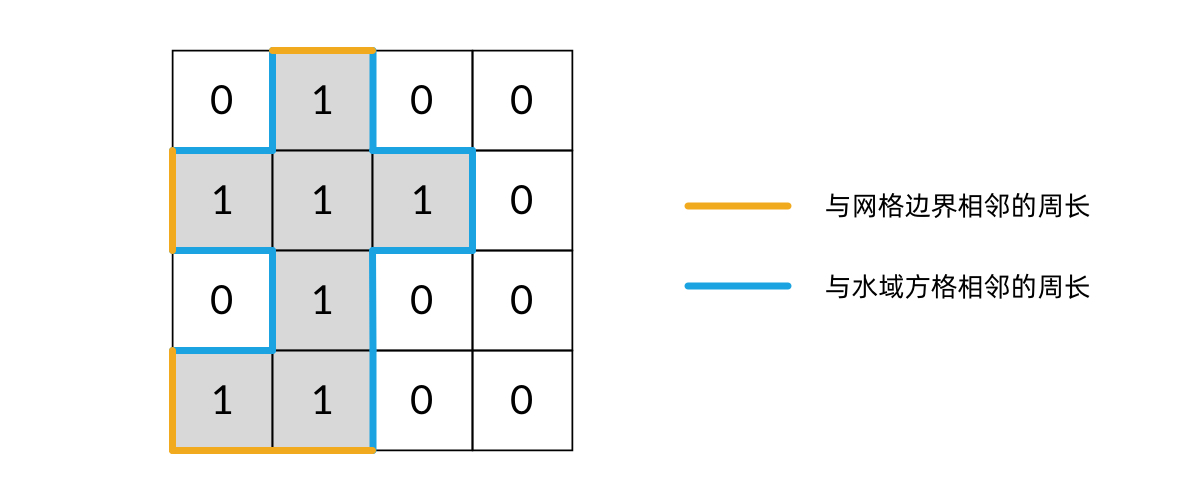
将这个“相邻关系”对应到 DFS 遍历中，就是：每当在 DFS 遍历中，从一个岛屿方格走向一个非岛屿方格，就将周长加 1。

// 执行耗时:10 ms,击败了48.91% 的Java用户
// 内存消耗:40.3 MB,击败了6.27% 的Java用户

class Solution {
    public int islandPerimeter(int[][] grid) {
        for (int r = 0; r < grid.length; r++){
            for (int c = 0; c < grid[0].length; c++){
                if(grid[r][c] == 1){
                    return dfs(grid, r, c);
                }
            }
        }
        return 0;
    }

    public int dfs(int[][] grid, int r, int c){
        if (!(0 <= r && r < grid.length && 0 <= c && c < grid[0].length)) {
            return 1;
        }  // 二维数组边界
        if (grid[r][c] == 0) {
            return 1;
        }  // 水域
        if (grid[r][c] != 1) {
            return 0;
        }  // 已遍历过的水域
        grid[r][c] = 2;  // 遍历过的岛屿就将其修改为2，防止进入死循环重复计算
        return dfs(grid, r - 1, c)
                + dfs(grid, r + 1, c)
                + dfs(grid, r, c - 1)
                + dfs(grid, r, c + 1);
    }
}