最最最详细的归并排序

归并排序详解

基本思想

利用归并的思想实现的排序算法，该算法采用经典的分治策略。分治法分为两个阶段，首先是分阶段，分阶段将问题分成一系列小的问题然后进行递归求解，然后是治阶段，治阶段将分阶段得到的各个答案“修补”在一起，这就是分而治之。

算法实现

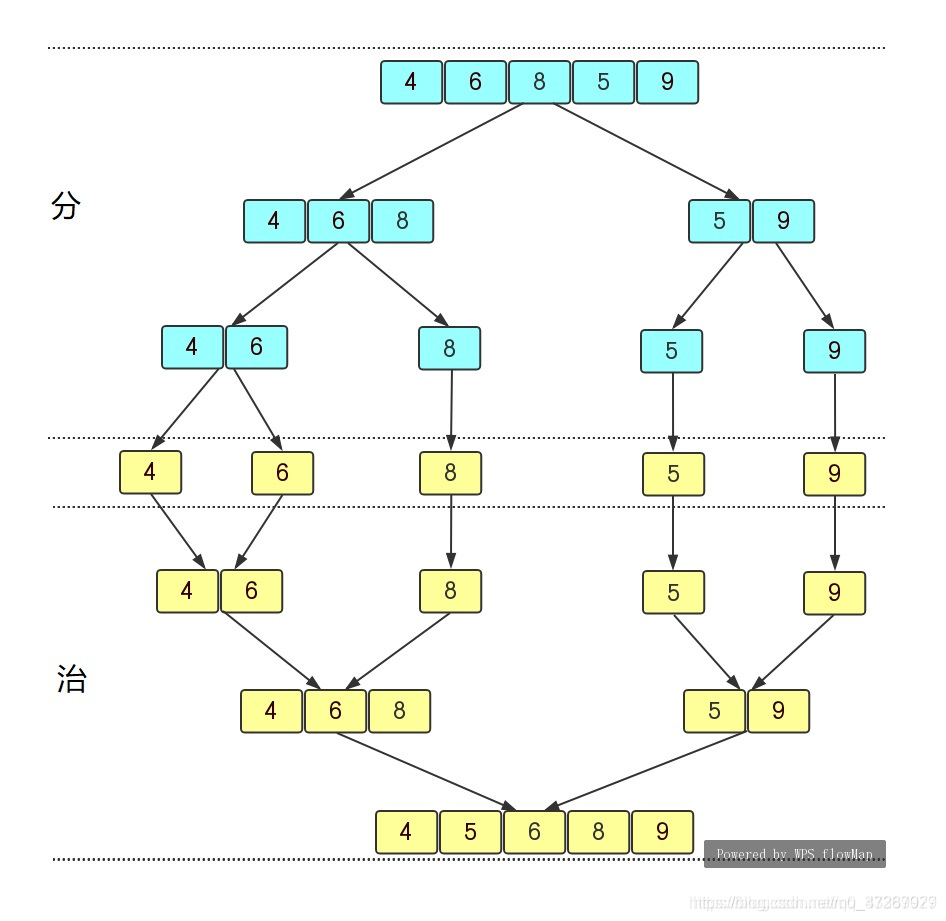
对于一个无序序列{4，6，8，5，9}我们使用分治策略可以画出如下图所示，可以看出这种结构很像一颗树，所以我们可以使用递归的方式去实现，分阶段是递归拆分子序列的过程，而治阶段则是将两个已经有序的子序列合并成一个有序的序列。

代码实现

#include <stdio.h>
#include <stdlib.h>

// 辅助函数：打印数组
void print_arr(int arr[], int n)
{
    for (int i = 0; i < n; i++)
    {
        printf("%d ", arr[i]);
    }
    putchar('\n');
}

// 合并
void merge(int arr[], int tempArr[], int left, int mid, int right)
{
    // 标记左半区第一个未排序的元素
    int l_pos = left;
    // 标记右半区第一个未排序的元素
    int r_pos = mid + 1;
    // 临时数组元素的下标
    int pos = left;

    // 合并
    while (l_pos <= mid && r_pos <= right)
    {
        if (arr[l_pos] < arr[r_pos]) // 左半区第一个剩余元素更小
            tempArr[pos++] = arr[l_pos++];
        else // 右半区第一个剩余元素更小
            tempArr[pos++] = arr[r_pos++];
    }

    // 合并左半区剩余的元素
    while (l_pos <= mid)
        tempArr[pos++] = arr[l_pos++];

    // 合并右半区剩余的元素
    while (r_pos <= right)
        tempArr[pos++] = arr[r_pos++];

    // 把临时数组中合并后的元素复制回原来的数组
    while (left <= right)
    {
        arr[left] = tempArr[left];
        left++;
    }
}

// 归并排序
void msort(int arr[], int tempArr[], int left, int right)
{
    // 如果只有一个元素，那么久不需要继续划分
    // 只有一个元素的区域，本生就是有序的，只需要被归并即可
    if (left < right)
    {
        // 找中间点
        int mid = (left + right) / 2;
        // 递归划分左半区
        msort(arr, tempArr, left, mid);
        // 递归划分右半区
        msort(arr, tempArr, mid + 1, right);
        // 合并已经排序的部分
        merge(arr, tempArr, left, mid, right);
    }
}

// 归并排序入口
void merge_sort(int arr[], int n)
{
    // 分配一个辅助数组
    int *tempArr = (int *)malloc(n * sizeof(int));
    if (tempArr) // 辅助数组分配成功
    {
        msort(arr, tempArr, 0, n - 1);
        free(tempArr);
    }
    else
    {
        printf("error: failed to allocate memory");
    }
}

int main(int argc, char const *argv[])
{
    int arr[] = {9, 5, 2, 7, 12, 4, 3, 1, 11};
    int n = 9;
    print_arr(arr, n);
    merge_sort(arr, n);
    print_arr(arr, n);

    return 0;
}