决策树原理

refer：第一章 决策树原理：1-决策树算法概述_哔哩哔哩_bilibili

决策树算法概述

决策树是一种解决分类问题的算法，采用树状结构，使用层层推理，实现最终分类。

例子：周末是否去公园野餐？
我们可能会按以下逻辑决策：

1. 今天天气晴朗吗？
   • 是 → 2. 温度高于 30℃吗？
     • 是 → 太晒了，不去
     • 否 → 适合野餐，去
   • 否 → 下雨 / 阴天，不去

这就是一个简单的决策树，每个 “问题” 是一个节点，每个 “答案” 是一条分支，最终结论是叶子节点。

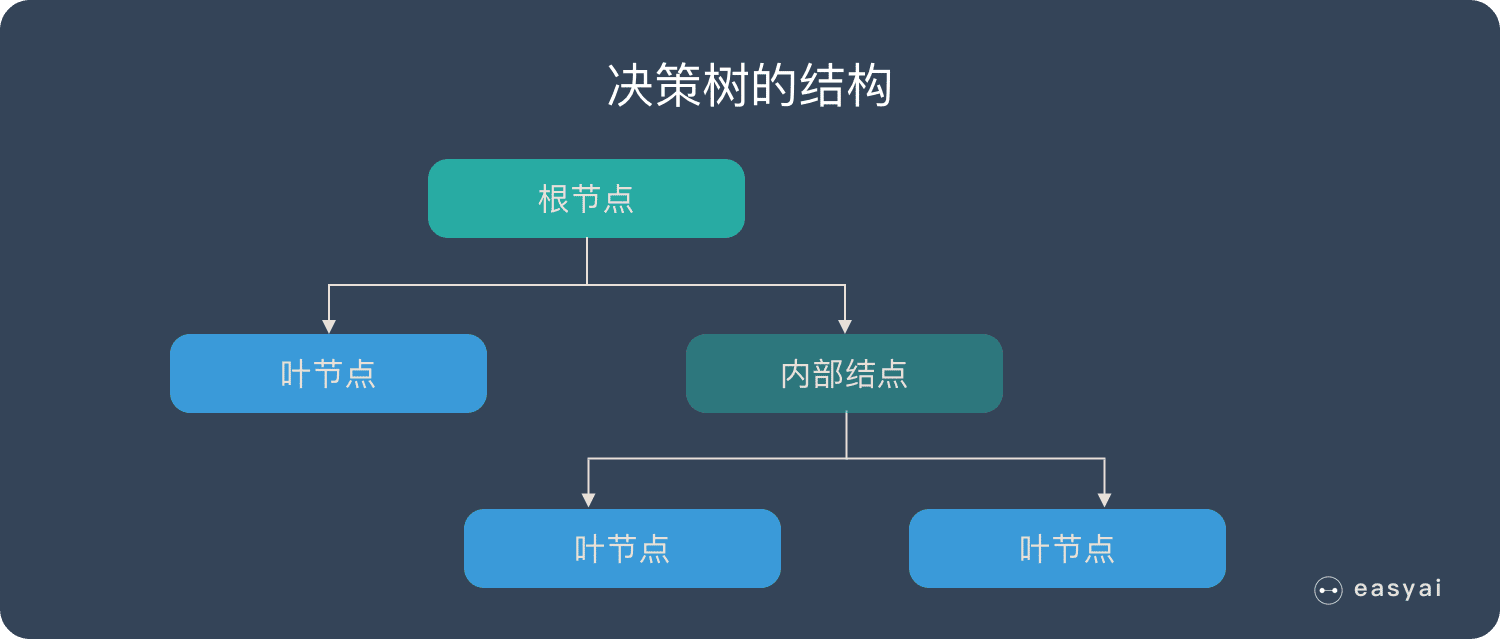
• 根节点：决策的起点（如 “天气晴朗吗？”）。
• 内部节点：中间的判断条件（如 “温度高于 30℃吗？”）。
• 叶子节点：最终的决策结果（如 “去” 或 “不去”）。
• 分支：每个判断的可能结果（如 “是” 或 “否”）。

熵的作用

问题：根节点该选择哪个特征？接下来呢？

目标：找到一种分类效果最好的特征作为判断条件。

衡量标准：熵

• 衡量数据的混乱程度（不确定性）。
• $ H(D) = - \sum_{i = 1}^{n} p_i \log_2 p_i $

决策树构造实例

数据：14天打球情况

特征：4种环境变化

目标：构造决策树

outlook	temperature	humidity	windy	play
sunny	hot	high	FALSE	no
sunny	hot	high	TRUE	no
overcast	hot	high	FALSE	yes
rainy	mild	high	FALSE	yes
rainy	cool	normal	FALSE	yes
rainy	cool	normal	TRUE	no
overcast	cool	normal	TRUE	yes
sunny	mild	high	FALSE	no
sunny	cool	normal	FALSE	yes
rainy	mild	normal	FALSE	yes
sunny	mild	normal	TRUE	yes
overcast	mild	high	TRUE	yes
overcast	hot	normal	FALSE	yes
rainy	mild	high	TRUE	no

划分方式：4种

问题：谁当根节点呢？

依据：信息增益

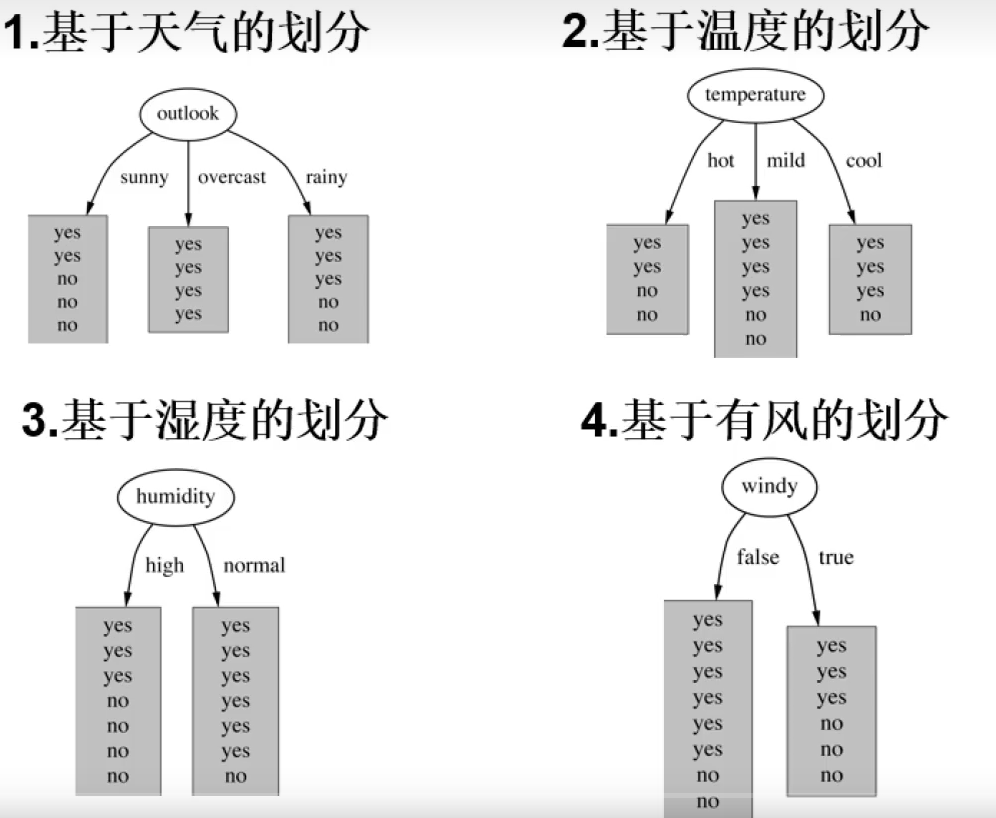
历史数据中，14天里有9天打球，5天不打球。

计算熵值：$ - \frac{9}{14} \log_2 \frac{9}{14} - \frac{5}{14} \log_2 \frac{5}{14} = 0.940 $

outlook特征：

outlook=sunny时，熵值为$ - \frac{2}{5} \log_2 \frac{2}{5} - \frac{3}{5} \log_2 \frac{3}{5} = 0.971 $

outlook=overcast时，熵值为 0

outlook=rainy时，熵值为$ - \frac{2}{5} \log_2 \frac{2}{5} - \frac{3}{5} \log_2 \frac{3}{5} = 0.971 $

加权计算熵值：$ \frac{5}{14} \times 0.971 \ + \frac{4}{14} \times 0 \ + \frac{5}{14}\times 0.971=0.693 $

信息增益：$ Gain(\text{outlook}) = 0.971-0.693=0.247 $

同样方法计算其他特征的信息增益，然后再比较，选择信息增益最大的那个当做判断条件

信息增益率与gini系数

• ID3：信息增益（有什么问题？它没法解决非常稀疏的特征（里边的种类非常多的时候））
• C4.5：信息增益率（解决ID3问题，考虑自身熵）$ \text{信息增益率} = \frac{\text{信息增益}}{\text{熵值}} $
• CART：使用GINI系数当作衡量标准，$ \text{Gini}(D) = 1 - \sum_{i = 1}^{n} p_i^2 $，值越小，效果越好

ID3 缺点：

• ID3 算法倾向于选择那些能把数据划分得最“细”的属性，即使这种划分对分类任务本身没有太大帮助，甚至会导致过拟合。
• 不能处理连续值属性，例如温度的具体数值（如 25.5℃, 30.1℃）或湿度的具体百分比（如 65%, 78%）。

剪枝方法

决策树过拟合风险很大，也就是分支会越来越多，使得每一个数据都是一个单独的叶节点。剪枝，顾名思义，就是减去多余的树枝。

预剪枝（更实用）

边构建决策树，边剪枝。在构建决策树的过程中，设置一些参数去控制树模型的增长，比如限制深度、限制叶节点个数、限制信息增益量等。

后剪枝

构造完决策树后，再剪枝。

构建一个复杂度惩罚项：$ \mathrm{Cost}_{\alpha}(T) = \text{误差}(T) + \alpha \times |T| $

• $ |T| $：树的叶子节点个数
• $ \alpha $越大，越倾向于剪枝

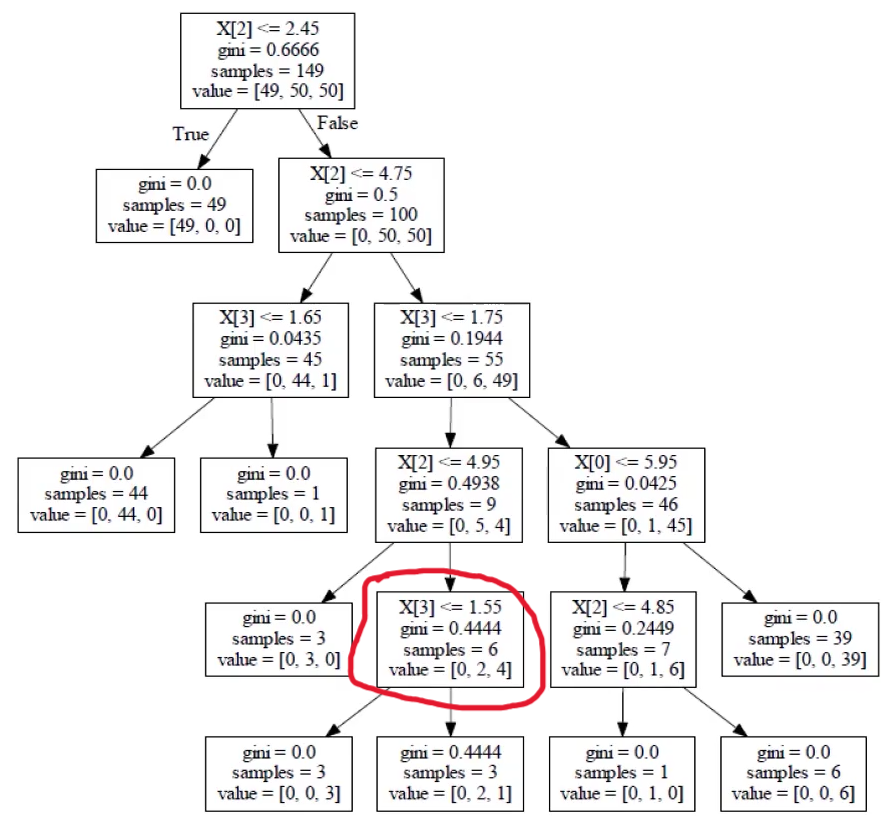
看圈起来的内部节点是否需要剪枝：

剪枝前：$ \mathrm{Cost}_{\alpha}(T) = 0 \times 3 \ + 0.444 \times 3 \ + 2 \times \alpha $

剪枝后：$ \mathrm{Cost}_{\alpha}(T) = 0.44 \times 6 \ + 1 \times \alpha $

比较损失大小（越大越不好），由$ \alpha $决定，这是我们自己给定的值。