吴恩达机器学习笔记-第一部分
前置知识
什么是机器学习
一句话解释:机器学习就是让计算机“像人一样”通过经验学习,不是我们手把手地教它每一步,而是让它自己从数据中总结规律。
监督学习(Supervised Learning)
定义
监督学习是指,我们在训练模型的时候,会告诉它“答案”是什么,模型通过这些已有的“题目+答案”来学习,以便将来遇到新题目时也能给出正确答案。
举例
想象你是一位老师,要教学生区分苹果🍎和橘子🍊。
你给学生看一堆水果,每个水果下面都写着标签:“这是苹果”或者“这是橘子”。
学生通过观察颜色、形状、大小等特征来学习,因为每个水果都有标签(答案),这就是“监督学习”。
在机器学习中:
| 输入(特征) | 输出(标签) |
|---|---|
| 颜色红、圆、较大 | 苹果 🍎 |
| 颜色橙、圆、较小 | 橘子 🍊 |
常见模型
回归(Regression)
回归模型的任务是“预测一个数值”,结果是连续的,不是分类的。
| 输入 | 回归模型预测的结果 |
|---|---|
| 房子的面积、位置、装修情况 | 预测房价是:152.3 万元 |
| 一辆车的品牌、年份、里程数 | 预测二手车价格:7.5 万元 |
| 一个城市的气温、湿度、风速 | 预测明天温度:28.4°C |
分类(Classification)
分类模型的任务是“选分类”:告诉你某个东西属于哪一类。
| 输入 | 分类模型预测的结果 |
|---|---|
| 一封电子邮件的内容 | “是垃圾邮件” or “不是垃圾邮件” |
| 一张动物照片 | “是猫” or “是狗” |
| 一位学生的学习数据 | “能及格” or “不及格” |
应用实例
- 垃圾邮件识别(输入:邮件内容,输出:垃圾/非垃圾)
- 图像识别(输入:照片,输出:狗🐶/猫🐱/人)
- 疾病预测(输入:检查数据,输出:是否患病)
无监督学习(Unsupervised Learning)
定义
无监督学习是指,我们在训练模型的时候,不给出答案,模型自己去观察、归类、找规律。
举例
你是一位老师,给学生一堆没写标签的水果,他们不知道哪些是苹果,哪些是橘子。
但学生发现:有些水果颜色偏红,有些偏橙;有些大有些小……于是学生把水果自己分成几类。
这就像是无监督学习:自己找规律分组。
在机器学习中:
| 输入(特征) | 没有输出标签,模型自己分组 |
|---|---|
| 颜色红、圆、较大 | 第1类 |
| 颜色橙、圆、较小 | 第2类 |
应用实例
- 客户分群(银行/电商将用户分成不同群体)
- 数据降维(去除冗余信息)
- 异常检测(比如检测工厂里的异常机器)
总结
| 对比点 | 监督学习 | 无监督学习 |
|---|---|---|
| 是否有“正确答案” | ✅ 有(带标签) | ❌ 没有(无标签) |
| 目的 | 预测结果 | 找结构、找规律 |
| 示例 | 判断水果种类(苹果/橘子) | 自己分水果群组 |
| 常见算法 | 线性回归、逻辑回归、决策树、SVM | 聚类(K-means)、主成分分析(PCA) |
监督学习-线性回归
什么是线性回归?
线性回归(Linear Regression) 是机器学习中最基础也是最重要的一种监督学习模型,用来预测一个连续的数值。
比如:
- 用房子的面积来预测房价。
- 用广告费用来预测销售额。
举个例子:
假设你是一个房产中介,你发现房子的价格(单位:万元)和面积(单位:平方米)之间有规律:
| 面积(x) | 价格(y) |
|---|---|
| 50 | 150 |
| 60 | 180 |
| 70 | 210 |
你希望找到一个公式,像这样的:
$ y = wx + b $
让你输入一个面积,就能预测价格。这个公式就是线性回归要学的目标。
线性回归的基本公式
线性回归的目标是学到一个函数(即模型):
$ \hat{y} = wx + b $
解释一下:
- x 是输入(如房子的面积)
- ŷ(y-hat) 是模型预测的结果
- w 是斜率(权重,表示每增加一单位x,y增加多少)
- b 是截距(当x=0时,y的值)
最终目标:让预测值 ŷ 尽可能接近真实值 y
代价函数
公式
\(J(w, b) = \frac{1}{2m} \sum_{i = 1}^{m} (\hat{y}^{(i)} - y^{(i)})^2 = \frac{1}{2m} \sum_{i = 1}^{m} (f_{w,b}(x^{(i)}) - y^{(i)})^2\)
直观理解

参数\(w\)(只有一个)不同时,代价函数\(J\)的变化:
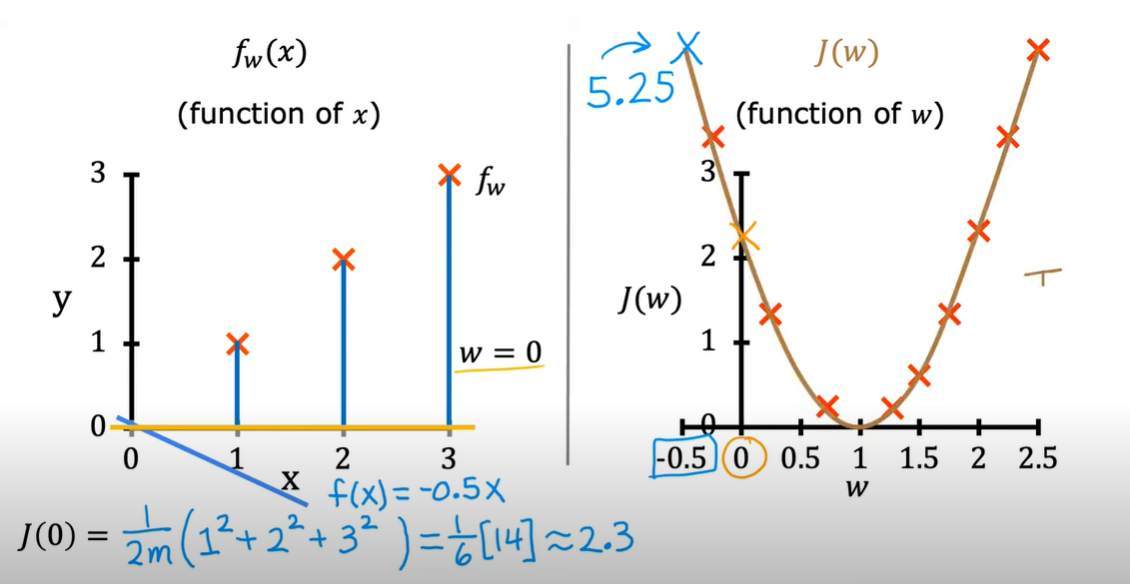
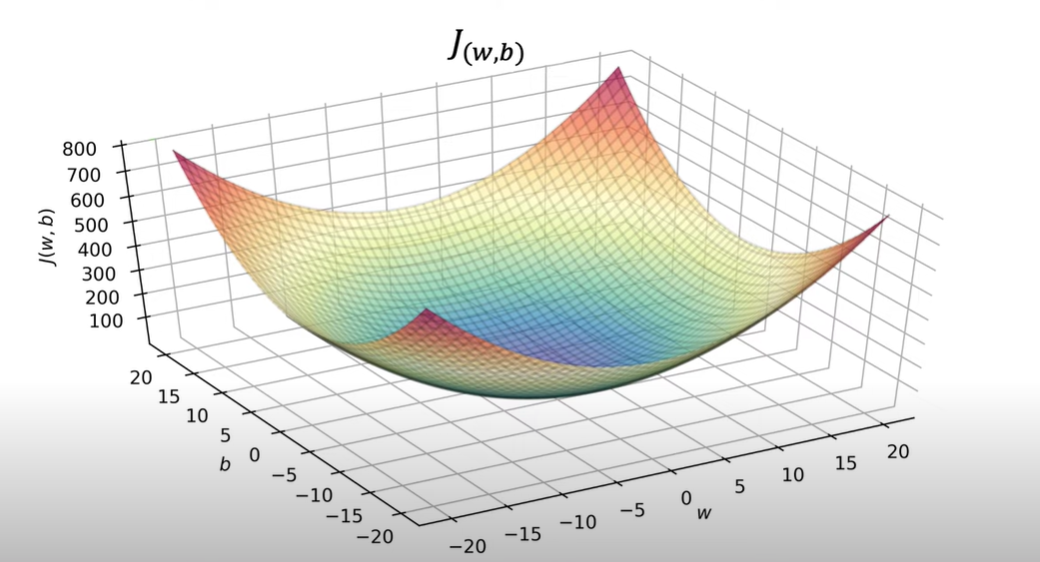
参数为\(w\)(只有一个)和\(b\)(只有一个):
代码示例(使用 Python 和 scikit-learn)
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
# 生成随机数据
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
# 创建线性回归模型
model = LinearRegression()
# 拟合模型
model.fit(X, y)
# 打印系数和截距
print("斜率 (m):", model.coef_[0][0])
print("截距 (b):", model.intercept_[0])
# 预测新数据
X_new = np.array([[1.5]])
y_pred = model.predict(X_new)
print("预测结果:", y_pred[0][0])
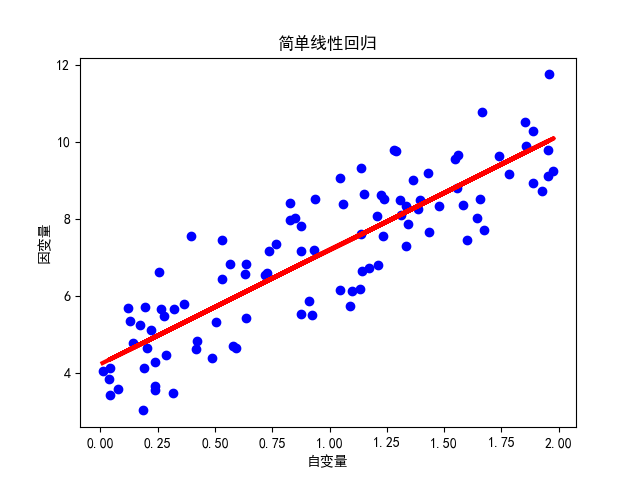
# 绘制散点图和拟合的直线
plt.scatter(X, y, color='blue')
plt.plot(X, model.predict(X), color='red', linewidth=3)
plt.xlabel("自变量")
plt.ylabel("因变量")
plt.title("简单线性回归")
plt.show()
运行结果:
斜率 (m): 2.968467510701019
截距 (b): 4.222151077447231
预测结果: 8.67485234349876
梯度下降算法
含义
梯度下降就是一个找最优解的过程。它一步一步地调整参数,直到代价函数的值最小为止。
直观理解
想象你站在一座山上, 任务是走到山谷底部(最低点) :
- 你的位置(坐标)是$ (w,b) $。
- 你脚下的坡度(梯度)告诉你:往哪个方向走,能最快下山(最陡的方向)。
- 梯度的值会随着你位置的变化而变化,所以每走一步都需要重新计算梯度,决定下一步往哪走。
这个“走下去”的过程就是梯度下降(Gradient Descent)
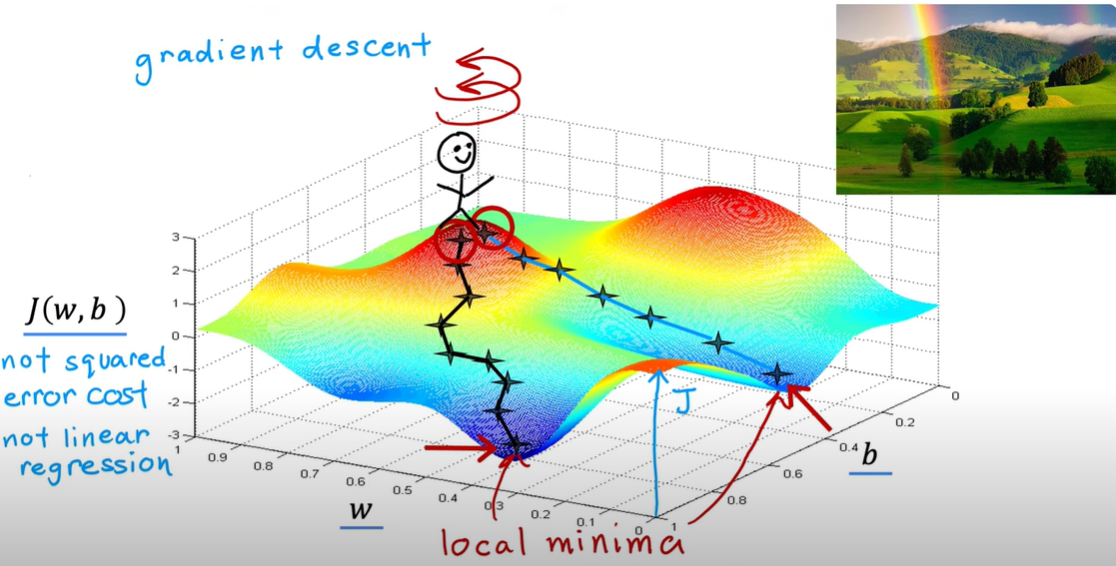
公式
- \({tmp_w} = w - \alpha \frac{\partial}{\partial w} J(w, b)=w - \alpha \frac{1}{m}\sum_{i = 1}^{m}(f_{w,b}(x^{(i)}) - y^{(i)})x^{(i)}\)
- \({tmp_b} = b - \alpha \frac{\partial}{\partial b} J(w, b)=b - \alpha \frac{1}{m}\sum_{i = 1}^{m}(f_{w,b}(x^{(i)}) - y^{(i)})\)
- \(w= tmp_w\)
- \(b=tmp_b\)
\(\frac{\partial}{\partial w} J(w, b)\)看成代价函数\(J\)的斜率。
例如,只有\(w\)一个参数:
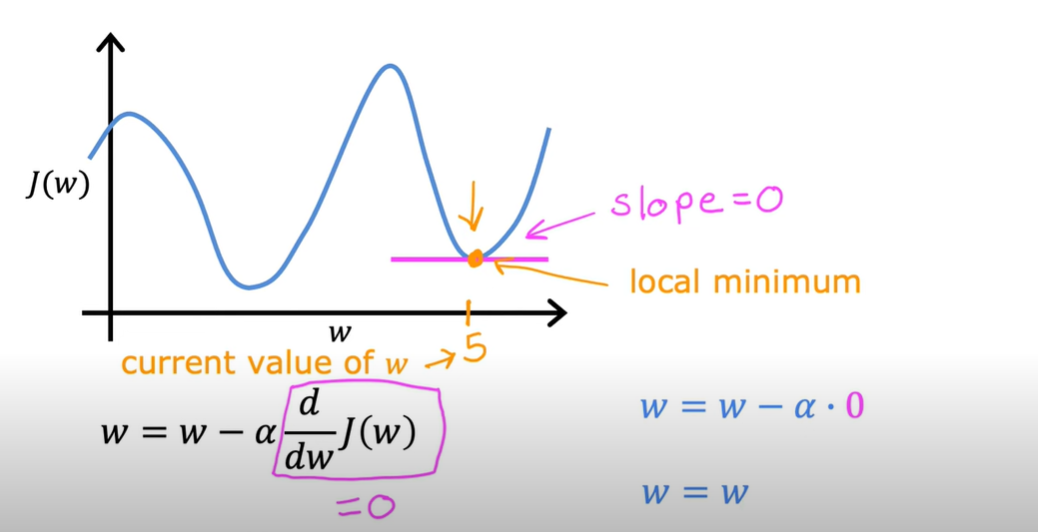
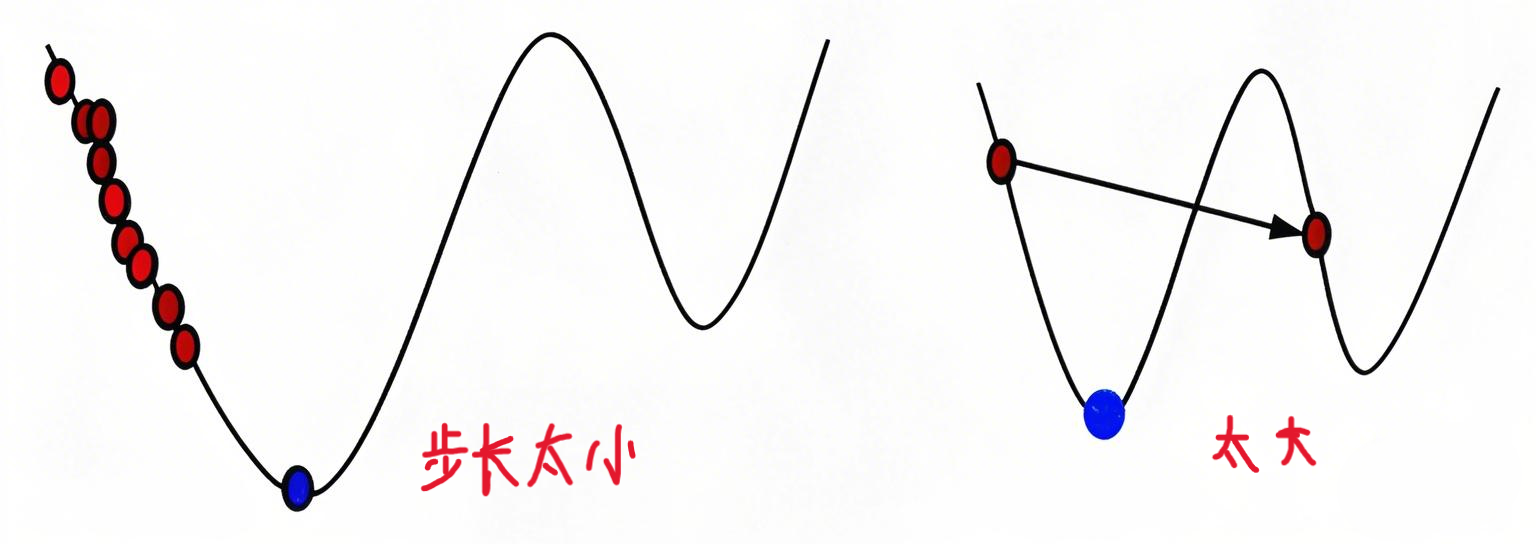
\(\alpha\)是学习率(learning rate),用来控制每次梯度下降时“走多远”。太小走得太慢,太大会错过最低点,需要找到合适的值。
示例代码(Python + NumPy 实现)
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
# 模拟训练数据(例如房子的面积和价格)
X = np.array([1, 2, 3, 4, 5]) # 特征(面积)
y = np.array([2, 4, 6, 8, 10]) # 标签(价格)
# 初始化参数
w = 0.0 # 斜率
b = 0.0 # 截距
# 学习率和迭代次数
alpha = 0.01
epochs = 100
# 存储损失记录(用于画图)
losses = []
# 梯度下降
for i in range(epochs):
# 预测值
y_pred = w * X + b
# 误差
error = y_pred - y
# 损失(均方误差)
loss = np.mean(error ** 2)
losses.append(loss)
# 计算梯度
dw = 2 * np.mean(error * X)
db = 2 * np.mean(error)
# 更新参数(就是你图中的公式)
w = w - alpha * dw
b = b - alpha * db
# 每10轮打印一次信息
if i % 10 == 0:
print(f"第{i}轮:w = {w:.4f}, b = {b:.4f}, loss = {loss:.4f}")
# 最终结果
print("\n训练完成:")
print(f"最终参数:w = {w:.4f}, b = {b:.4f}")
# 可视化结果
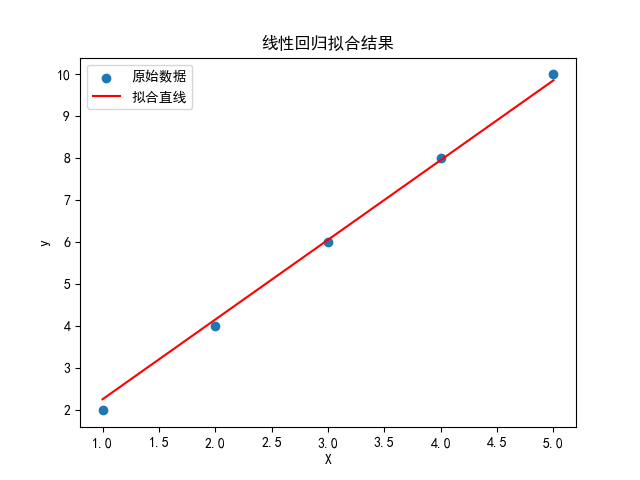
plt.scatter(X, y, label='原始数据')
plt.plot(X, w * X + b, color='red', label='拟合直线')
plt.legend()
plt.xlabel('X')
plt.ylabel('y')
plt.title('线性回归拟合结果')
plt.show()
输出结果:
第0轮:w = 0.4400, b = 0.1200, loss = 44.0000
第10轮:w = 1.7674, b = 0.4693, loss = 0.2435
第20轮:w = 1.8609, b = 0.4774, loss = 0.0430
第30轮:w = 1.8713, b = 0.4631, loss = 0.0393
第40轮:w = 1.8759, b = 0.4478, loss = 0.0367
第50轮:w = 1.8801, b = 0.4329, loss = 0.0343
第60轮:w = 1.8841, b = 0.4185, loss = 0.0321
第70轮:w = 1.8880, b = 0.4045, loss = 0.0300
第80轮:w = 1.8917, b = 0.3911, loss = 0.0280
第90轮:w = 1.8953, b = 0.3780, loss = 0.0262
训练完成:
最终参数:w = 1.8984, b = 0.3667
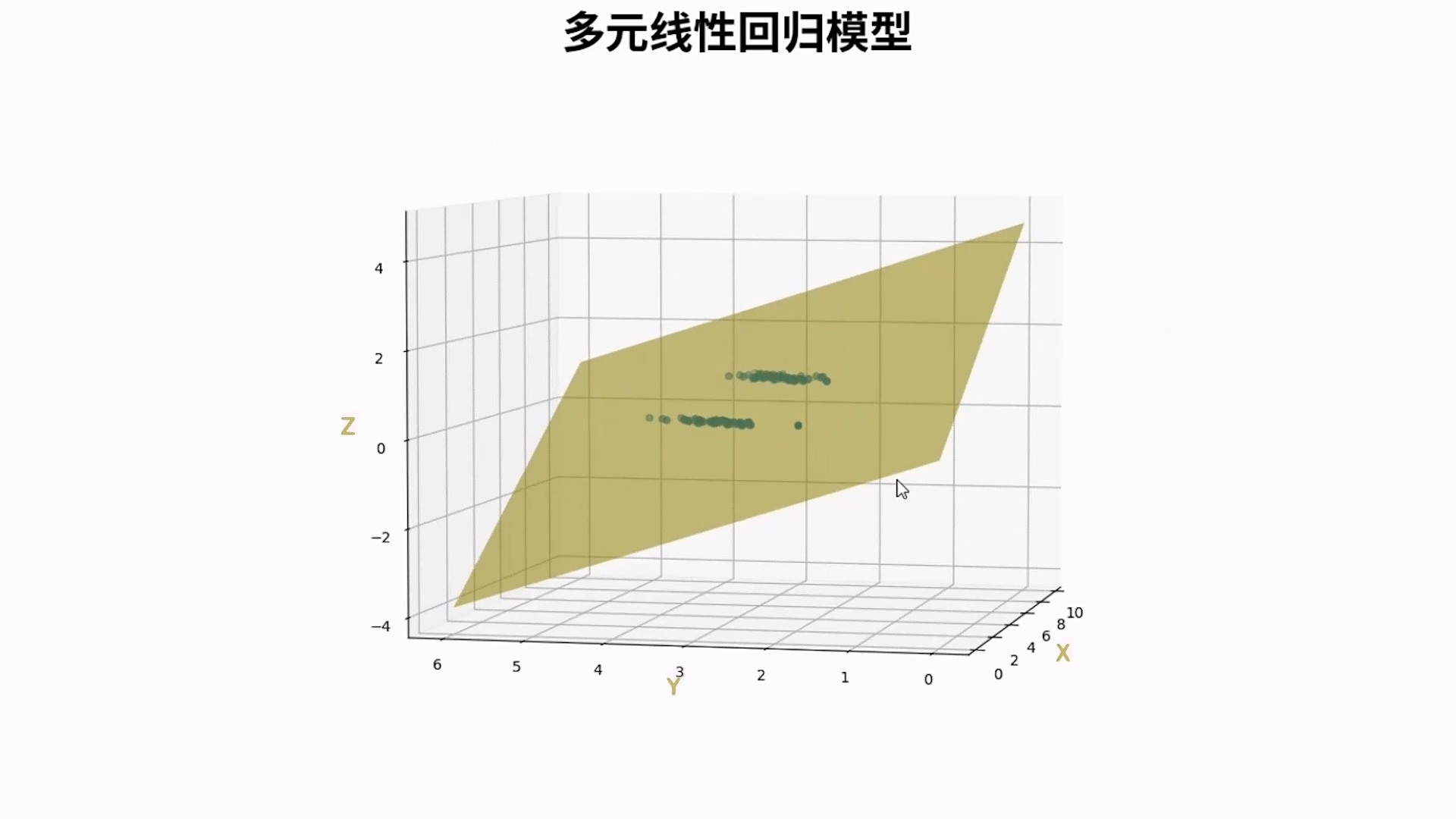
多元线性回归(Multiple Linear Regression)
多元线性回归是线性回归的扩展,它可以处理多个输入特征(变量),而不是只有一个特征。
基本形式
\(f_{\vec{w},b}(\vec{x}) = w_1x_1 + w_2x_2 + \cdots + w_nx_n + b = \vec{w} \cdot\ \vec{x} + b\)
- \(\vec{w} = (w_1,w_2, \dots ,w_n)\):输入的特征向量,比如房子的信息:面积、卧室数、楼层数、地段评分等。
- \(\vec{x} = (x_1,x_2, \dots ,x_n)\):模型的参数(权重),每个特征对应一个权重。
python代码实现点乘
f = np.dot(w, x) + b
举例
假设我们要预测房价:
| 特征 | 值 |
|---|---|
| 房子面积(㎡) | $ x_1 = 100 $ |
| 卧室数 | $ x_2 = 3 $ |
| 距离市中心(km) | $ x_3 = 8 $ |
模型参数是:
\(\vec{w} = [3000, 10000, -2000]\),\(\ b = 50000\)
那么预测房价为:
\(f(\vec{x}) = 3000 \cdot 100 + 10000 \cdot 3 + (-2000) \cdot 8 + 50000 = 300000 + 30000 - 16000 + 50000 = 364000\)
示例代码
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
plt.rcParams['font.sans-serif'] = ['SimHei'] # 正常显示中文
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
# 原始数据:面积(m²)、卧室数、距离市中心(km)
X = np.array([
[100, 3, 8],
[120, 2, 5],
[80, 4, 10],
[150, 3, 7],
[200, 5, 2]
])
y = np.array([300, 320, 260, 390, 500]) # 房价,单位万元
# ✅ 标准化特征(Z-score 标准化)
X_mean = np.mean(X, axis=0)
X_std = np.std(X, axis=0)
X_scaled = (X - X_mean) / X_std
# 初始化参数
m, n = X_scaled.shape
w = np.zeros(n)
b = 0.0
# 超参数
alpha = 0.01
epochs = 1000
loss_list = []
# ✅ 梯度下降训练
for epoch in range(epochs):
y_pred = np.dot(X_scaled, w) + b
error = y_pred - y
loss = np.mean(error ** 2)
loss_list.append(loss)
# 计算梯度
dw = (2/m) * np.dot(X_scaled.T, error)
db = (2/m) * np.sum(error)
# 更新参数
w -= alpha * dw
b -= alpha * db
# 每 100 轮打印一次
if epoch % 100 == 0:
print(f"第 {epoch:>4} 轮: loss = {loss:.4f}, w = {w}, b = {b:.4f}")
print("\n✅ 模型训练完成!")
print(f"最终参数:w = {w}, b = {b:.4f}")
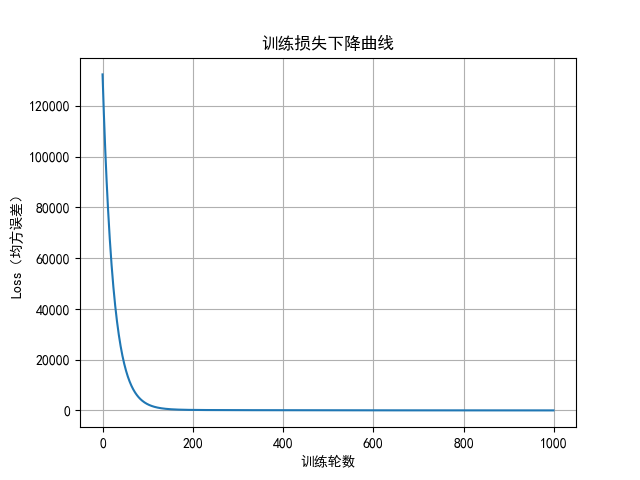
# ✅ 可视化 Loss 曲线
plt.plot(range(epochs), loss_list)
plt.xlabel("训练轮数")
plt.ylabel("Loss(均方误差)")
plt.title("训练损失下降曲线")
plt.grid(True)
plt.show()
# ✅ 预测函数
def predict(new_X):
new_X_scaled = (new_X - X_mean) / X_std
return np.dot(new_X_scaled, w) + b
# 示例预测
new_house = np.array([130, 3, 6])
predicted_price = predict(new_house)
print(f"🏠 对面积130平米、3个卧室、距离6公里的房子预测价格为:{predicted_price:.2f} 万元")
# ✅ 与 sklearn 对比
reg = LinearRegression()
reg.fit(X_scaled, y)
print("\n📘 sklearn 线性回归模型:")
print(f"权重 w = {reg.coef_}")
print(f"偏置 b = {reg.intercept_:.4f}")
运行结果:
第 0 轮: loss = 132420.0000, w = [ 1.67809416 0.90997887 -1.46353821], b = 7.0800
第 100 轮: loss = 2440.6073, w = [ 44.4786325 17.43832645 -30.28374442], b = 307.9916
第 200 轮: loss = 209.7314, w = [ 50.89536614 15.44639964 -25.89241122], b = 347.8984
第 300 轮: loss = 126.3587, w = [ 55.84166938 14.08348652 -21.56379231], b = 353.1908
第 400 轮: loss = 93.3602, w = [ 59.9963053 13.04402769 -17.84495093], b = 353.8927
第 500 轮: loss = 70.2485, w = [ 63.50374323 12.18926644 -14.68980171], b = 353.9858
第 600 轮: loss = 53.7416, w = [ 66.46773844 11.47167583 -12.02029357], b = 353.9981
第 700 轮: loss = 41.9463, w = [68.97309129 10.8661047 -9.76319295], b = 353.9997
第 800 轮: loss = 33.5177, w = [71.09089519 10.35441161 -7.85510148], b = 354.0000
第 900 轮: loss = 27.4947, w = [72.88112516 9.92190737 -6.24211781], b = 354.0000
✅ 模型训练完成!
最终参数:w = [74.38054529 9.55966893 -4.89114575], b = 354.0000
🏠 对面积130平米、3个卧室、距离6公里的房子预测价格为:350.97 万元
📘 sklearn 线性回归模型:
权重 w = [82.66522249 7.55822433 2.57332822]
偏置 b = 354.0000
特征缩放(feature scaling)
特征缩放
公式
\(x' = \frac{x}{\text{max} }\)
其中:
- \(x\)是原始特征值
- \(max\)是该特征的最大值
直观理解
如果你想预测房价,现在有两个变量 x1 和 x2 来控制房子的价格。 x1 为房子的大小,范围在 0 到 2000,x2 为房子中卧室的数目,范围在 0 到 5,那么画出这个代价函数的轮廓图就是这个样子,一个扁扁的椭圆形。
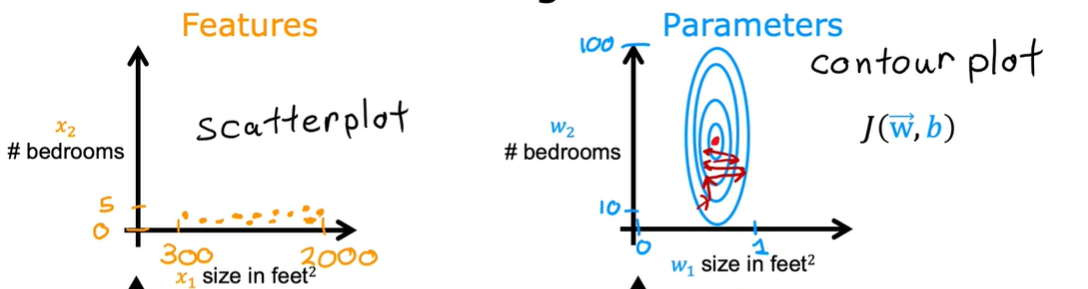
对这个函数进行梯度下降,就是红线的过程,你会发现,这个路程很长很曲折,这样我们进行梯度下降所花费的时间就会很长。
这里就要用到特征缩放(Feature Scaling)。将变量 x1 和 x2 都缩放到一个范围中,我们将他们都缩放到 -1 到 1 这个范围内。最简单的方法就是将 x1 除以 2000(因为他的范围就是 0-2000), x2 除以 5。
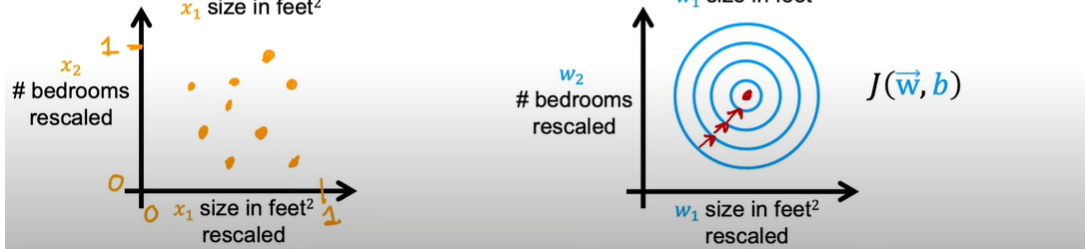
均值归一化(Mean normalization)
\(x' = \frac{x - \mu}{\text{max} - \text{min}}\)
其中:
● \(x\)是原始特征值
● \(μ\)是该特征的平均值(mean)
● \(max\)、\(min\)是该特征的最大值与最小值
Z-score归一化
\(x' = \frac{x - \mu}{\sigma}\)
其中:
● \(x\)是原始特征值
● \(μ\)是该特征的平均值(mean)
● \(\sigma\)是特征的标准差(standard deviation)
特征工程
含义
特征工程就是把原始数据变成机器学习模型能更好理解和利用的“特征”的过程
举例
原始数据表格(房价预测):
| 面积(m²) | 建成年份 | 楼层信息 | 距离市中心(km) |
|---|---|---|---|
| 120 | 2005 | 高楼层 | 8 |
经过特征工程后,你可能会变成:
| 面积(m²) | 房龄(年) | 是否高楼层(0/1) | 距离市中心(km) |
|---|---|---|---|
| 120 | 19 | 1 | 8 |
你看到了什么?
- 把“建成年份”变成了“房龄” = 2024 - 2005
- 把文字“高楼层”变成了数值 1(方便模型识别)
- 去掉了冗余不必要的信息
- 👉 这些就是特征工程的基本思想!
逻辑回归(Logistic Regression)
逻辑回归
含义
逻辑回归是用来做分类的模型,能判断样本属于某个类别的概率。
公式
\(z=\vec{w} \cdot \vec{x} + b\)
\(g(z) \ = \frac{1}{1 + e^{-z}}\)
\(f_{\vec{w},b}(\vec{x}) = g(\vec{w} \cdot \vec{x} + b) \ = \frac{1}{1 + e^{-(\vec{w} \cdot \vec{x} + b)}}\)
直观理解

目标:输出在 0 到 1 之间
- 分类问题中,我们希望模型的输出表示“属于某一类的概率”。
- 概率自然应该在区间 (0, 1) 之间,所以需要一种“压缩函数”。
Sigmoid 函数(Logistic 函数)
图中公式:
\(g(z) = \frac{1}{1 + e^{-z}}\)
- 当\(z→+∞\),\(g(z)→1\)
- 当\(z→-∞\),\(g(z)→0\)
- 当\(z→0\),\(g(z)→0.5\)
决策边界(decision boundary)
含义
决策边界 是逻辑回归用来 把不同类别分开 的“分界线”
条件
\(z = \vec{w} \cdot \vec{x} + b = 0\)
举例
(1)
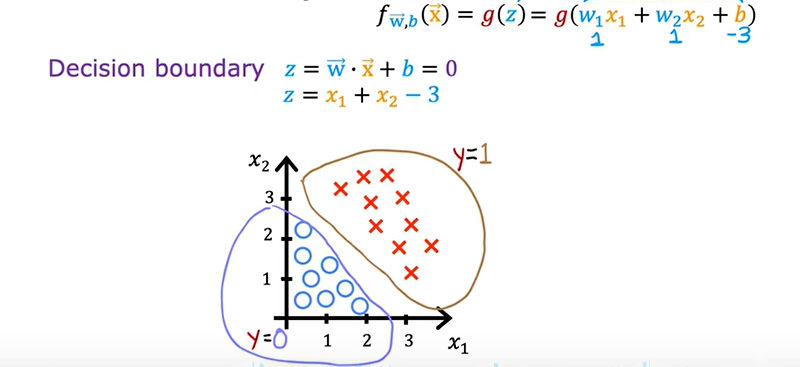
(2)

(3)
还有很多,如椭圆、不规则的。。。
逻辑回归的代价函数
公式
\(J(\vec{w}, b) = \frac{1}{m} \sum_{i = 1}^{m} L(f_{\vec{w}, b}(\vec{x}^{(i)}), y^{(i)})\)
损失函数
\(L(f_{\vec{w}, b}(\vec{x}^{(i)}), y^{(i)}) = \begin{cases} -\log(f_{\vec{w}, b}(\vec{x}^{(i)})) & \text{if } y^{(i)} = 1 \\ -\log(1 - f_{\vec{w}, b}(\vec{x}^{(i)})) & \text{if } y^{(i)} = 0 \end{cases}\)
其中:
- \(f \in (0, 1)\):模型预测值(即 sigmoid 输出)
- \(y \in \{0, 1\}\):真实标签
- 我们希望\(f\)接近\(y\)的值
如果\(f\)和\(y\)的值相差越大,损失就越大。
直观理解
\(-\log(f)\):
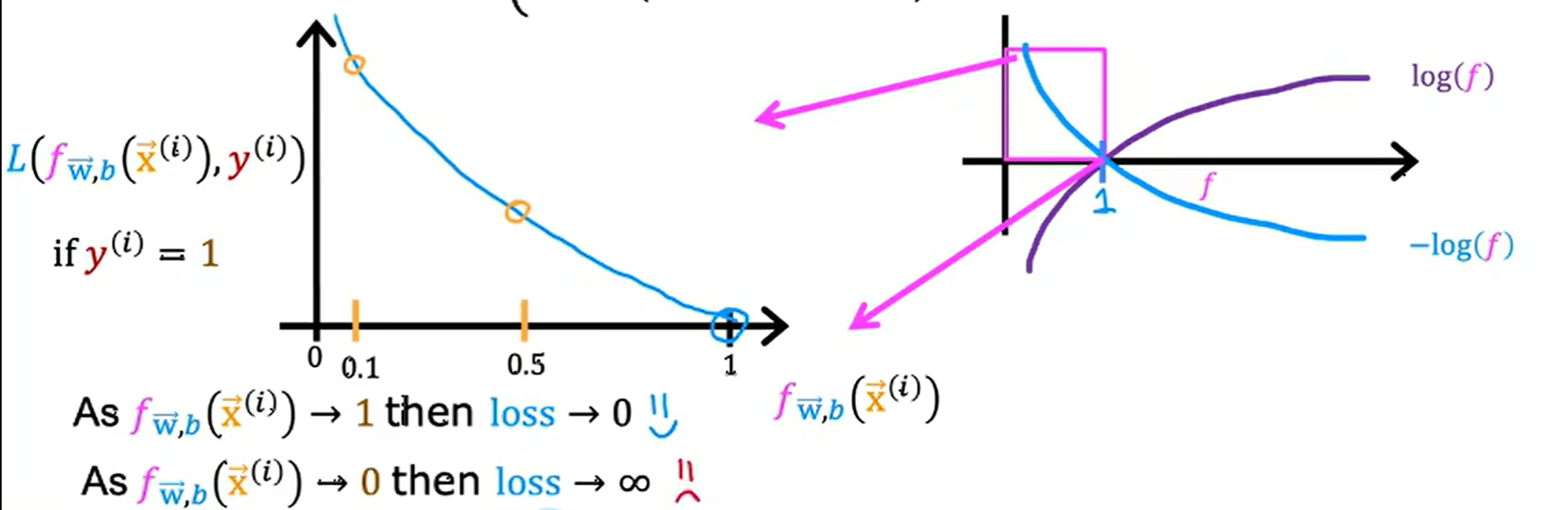
\(-\log(1-f)\):
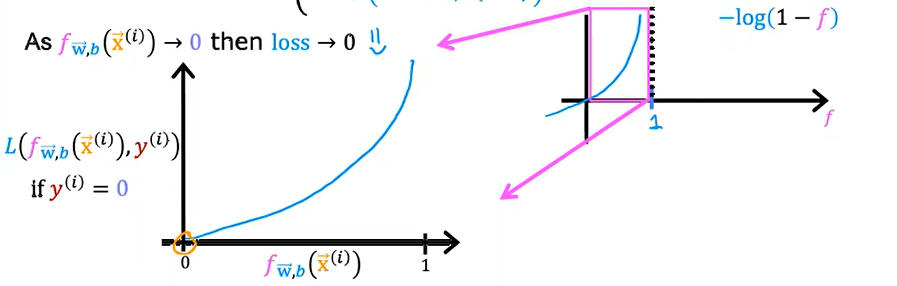
简化公式
\(J(\vec{w}, b) = - \frac{1}{m} \sum_{i = 1}^{m} \left[ y^{(i)} \log(f_{\vec{w}, b}(\vec{x}^{(i)})) + (1 - y^{(i)}) \log(1 - f_{\vec{w}, b}(\vec{x}^{(i)})) \right]\)
\(L(f_{\vec{w}, b}(\vec{x}^{(i)}), y^{(i)}) = -y^{(i)} \log(f_{\vec{w}, b}(\vec{x}^{(i)})) - (1 - y^{(i)}) \log(1 - f_{\vec{w}, b}(\vec{x}^{(i)}))\)
梯度下降实现
重复{
\(w_j = w_j - \alpha \left[ \frac{1}{m} \sum_{i = 1}^{m} \frac{1}{2} (f_{\vec{w}, b}(\vec{x}^{(i)}) - y^{(i)}) x_j^{(i)} \right]\)
\(b = b - \alpha \left[ \frac{1}{m} \sum_{i = 1}^{m} \frac{1}{2} (f_{\vec{w}, b}(\vec{x}^{(i)}) - y^{(i)}) \right]\)
}
过拟合问题(Overfitting Problem)
直观理解
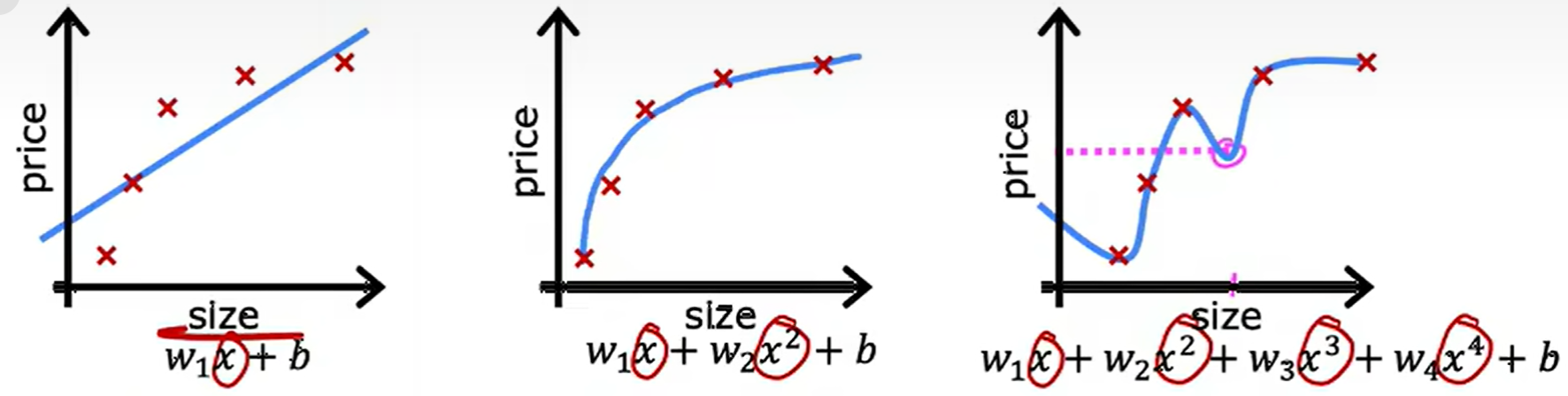
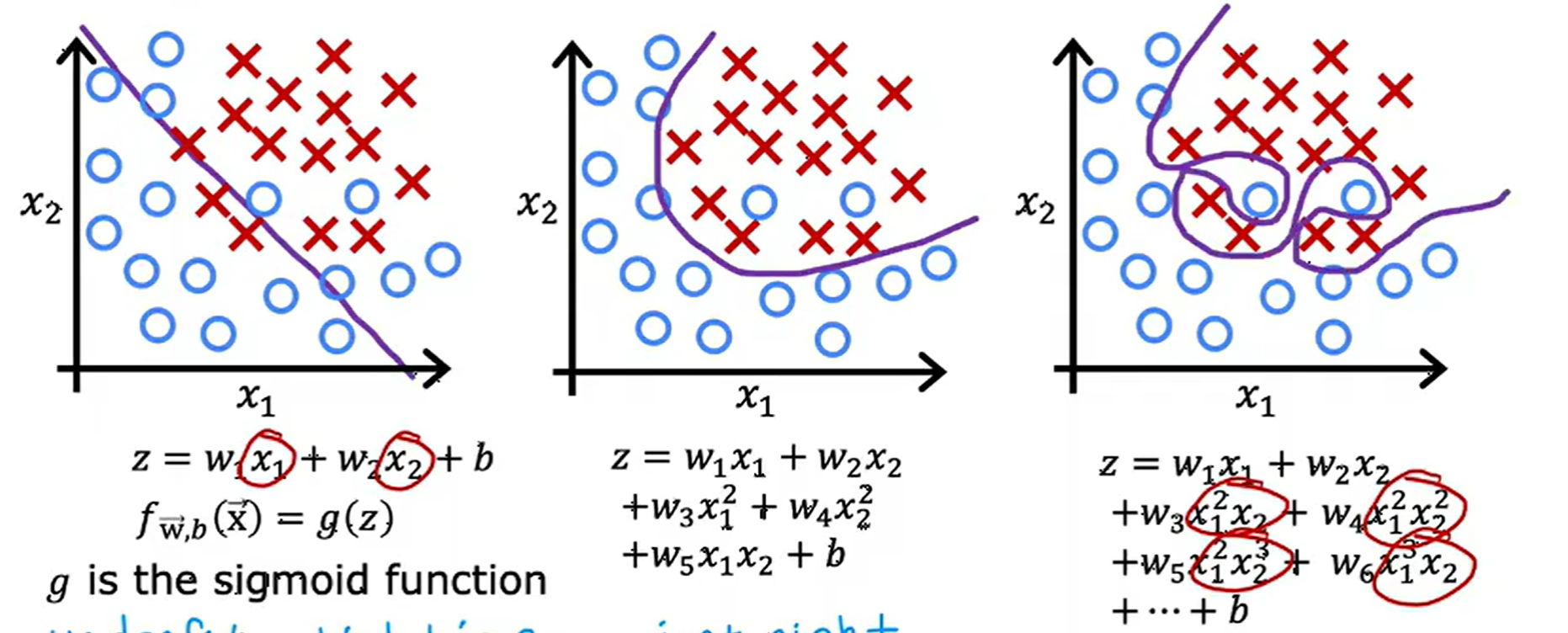
左边“欠拟合”,中间“恰到好处”,右边“过拟合”
解决过拟合方法
- 收集更多的数据
- 减少特征数量, 使用更简单的模型
- 使用正则化(Regularization)减小参数大小
正则化(Regularization)
正则化代价函数
\(\lambda\)称为正则化参数(Regularization Parameter)
线性回归
\(J(\vec{w}, b) = \frac{1}{2m} \sum_{i = 1}^{m} (f_{\vec{w}, b}(\vec{x}^{(i)}) - y^{(i)})^2 + \frac{\lambda}{2m} \sum_{j = 1}^{n} w_j^2\)
逻辑回归
\(J(\vec{w}, b) = - \frac{1}{m} \sum_{i = 1}^{m} \left[ y^{(i)} \log(f_{\vec{w}, b}(\vec{x}^{(i)})) + (1 - y^{(i)}) \log(1 - f_{\vec{w}, b}(\vec{x}^{(i)})) \right] + \frac{\lambda}{2m} \sum_{j = 1}^{n} w_j^2\)
正则化线性回归
重复{
\(w_j = w_j - \alpha \left[ \frac{1}{m} \sum_{i = 1}^{m} \left[ (f_{\vec{w}, b}(\vec{x}^{(i)}) - y^{(i)}) x_j^{(i)} \right] + \frac{\lambda}{m} w_j \right]\)
\(b = b - \alpha \frac{1}{m} \sum_{i = 1}^{m} (f_{\vec{w}, b}(\vec{x}^{(i)}) - y^{(i)})\)
}
正则化逻辑回归
重复{
\(w_j = w_j - \alpha \left[ \frac{1}{m} \sum_{i = 1}^{m} \left[ (f_{\vec{w}, b}(\vec{x}^{(i)}) - y^{(i)}) x_j^{(i)} \right] + \frac{\lambda}{m} w_j \right]\)
\(b = b - \alpha \frac{1}{m} \sum_{i = 1}^{m} (f_{\vec{w}, b}(\vec{x}^{(i)}) - y^{(i)})\)
}
虽然看上去和“正则化线性回归”相同,但是函数\(f\)不一样,这是应用于\(z\)的逻辑回归函数



 浙公网安备 33010602011771号
浙公网安备 33010602011771号