第一单元总结

第一单元总结

目录

目录

• 第一单元总结
  • 目录
  • 作业分析
  • 整体架构
    • 架构思路
    • 整体架构
      • 这种架构是如何拆括号的？
      • 这种架构的优缺点是什么？
    • 其他架构的讨论
  • 架构的迭代
  • 程序结构分析
    • 第一次作业
      • 代码规模
      • 复杂度分析
    • 第二次作业
      • 代码规模
      • 复杂度分析
    • 第三次作业
      • 代码规模
      • 复杂度分析
      • 静态分析
  • 测试与bug
    • 范式不唯一
    • 变量名冲突
    • 可变对象
  • 心得体会

作业分析

本单元三次作业的任务是，输入一个满足形式化定义的字符串\(Expre\)，按数学意义将其解读，并拆去所有括号。可能含有自定义函数、求和函数、三角函数、幂函数。

第三次作业的形式化定义如下：

\[\begin{aligned} Expre &\rightarrow [+|-]Term \lbrace (+|-)Term \rbrace \\ Term &\rightarrow [+|-]Factor \lbrace * Factor \rbrace \\ Factor &\rightarrow ConstFactor\;|\;ExprFactor\;|\;VarFactor\\ ConstFactor &\rightarrow SignedInt \\ ExprFactor &\rightarrow (Expre)[Index]\\ VarFactor &\rightarrow PowerFunct \;|\; TriFunct \;|\; SumFunct \;|\; CustomFunctCall \\ PowerFunct &\rightarrow Var \;|\; i \;\; [Index] \\ TriFunct &\rightarrow sin(Factor) \;|\; cos(Factor) \;\; [Index] \\ SumFunct &\rightarrow sum(i, ConstFactor, ConstFactor, Factor) \\ CustomFunctCall &\rightarrow FunctName(Factor\lbrace , Factor \rbrace ) \\ CustomFunctDef &\rightarrow FunctName(Var \lbrace ,Var\rbrace ) = Expre \\ Index &\rightarrow **[+]Int\\ Int &\rightarrow (0|1|2|3|4|5|6|7|8|9)\lbrace 0|1|2|3|4|5|6|7|8|9 \rbrace \\ SignedInt &\rightarrow [+|-]Int\\ Var &\rightarrow x\;|\;y\;|\;z\\ FunctName &\rightarrow f\;|\;g\;|\;h\\ \\ \end{aligned} \]

整体架构

架构思路

该单元的作业中，我的架构思路来自第一次作业。第一次作业中，由于没有三角函数、求和函数和自定义函数，因此拆括号的结果一定是一个多项式。因此，这个单元的整体架构都基于最终计算结果的范式。

具体来说，虽输入的是一个可能包含括号和函数嵌套的表达式，但拆括号的最终结果一定是一个形如

\[\sum_j k_j \prod_i f_{j,i}^{p_{j,i}},\;\;f_{j,i}=x\text{或}sin(Expre)\text{或}cos(Expre) \]

的式子。若称\(\prod_i f_{j,i}^{p_{j,i}}\)为NormalTerm（项范式），则最终的结果一定是若干个NormalTerm的线性组合。因此，我将这种结构单独抽象出来，作为与输入表达式层次化结构基本独立的模块进行操作。

我的设计的特点在于，将输入的表达式与数学意义上的表达式作为两种不同的、独立的结构进行设计。由于输入的表达式可能含有很多复杂的嵌套关系（也可能含有一些括号），不过最终化得的表达式形式的确定的，因此，只需按照结果的确定形式对其进行建模，实现加法、乘法等方法，之后再在输入表达式中递归地实现转换方法，不断调用已经实现的加法乘法等方法，即可完成表达式拆除括号，和基本的合并化简。

整体架构

UML类图如下：

将程序分为三个包：

1. parser: 按文法解析输入
2. sentence: 输入表达式，按给定的结构层次存储
3. mathexpression: 数学表达式，实现了加法、乘法运算

在parser包中，使用递归下降法，解析输入的字符串。其中的lexer类用于识别字符串中的不同组件，parser类中有一系列解析方法，用于递归
下降地解析，最终返回sentence.Expre类的表达式。

sentence包中的各个类均是直接按照输入字符串的文法定义进行构造的，逻辑上只是按结构储存输入的字符串，而非其对应的数学意义上的表达式，这也是该包命名为"sentence"而非"expression"的原因。

从类图中可以看出，sentence包内部类的设计与形式化定义所完全吻合。最上方是Expre类，表示输入的“表达式”，它由若干个Term（输入的“项”）构成，每个Term又由一些Factor组成，ConstFactor、ExprFactor、Function是Factor的三种具体类型，Function又分为TriFunct和PowerFunct。这里没有出现自定义函数调用和求和函数类，这两种情况统一留给了parser在解析时直接将自定义函数和求和函数展开成一般的表达式因子ExprFactor。

值得注意的是，TriFunct内部和ExprFactor内部仍然有可能含有Expre类型的数据，即会有结构层次上的嵌套关系，从类图种也可看到这一点。由于我们想要描述的对象是一个“表达式”，而表达式中会存在这种嵌套关系，因此我们的程序中无法摆脱这一个结构层次上的嵌套。

mathexpression包主要描述了数学表达式。顶层为MathExpre，该表达式是若干个NormalTerm的线性组合。每个NormalTerm包含了若干个三角函数或变元的幂，它们统一实现了TermElement接口。再NormalTerm中使用HashMap储存底数与幂的关系，在MathExpre中依然使用HashMap储存NormalTerm及其系数的关系。即使用两层的HashMap来存储一个数学表达式。在MathExpre中，实现了若干加法、乘法的方法。

这种架构是如何拆括号的？

sentence包内部的所有类都实现了一个toMathExpre方法，该方法将当前对象转换为数学表达式，并返回一个mathexpression.MathExpre类的数据。

假设现在调用了Expre中的toMathExpre方法，该方法内部会调用该Expre中包含的的每一个Term的toMathExpre方法，获得该表达式含有的所有的项的数学表达式。由于一个表达式由若干个项相加得到，因此我们调用每一个项的数学表达式中的加法方法，将所有的MathExpre相加，得到该Expre的最终MathExpre结果。

若现在调用了Term中的toMathExpre方法，该方法又会调用该项中包含的每一个因子的ToMathExpre方法，并调用数学表达式类中的乘法方法，将每个因子对应的数学表达式相乘，得到该Term的最终MathExpre结果。

这种架构的优缺点是什么？

无论多么复杂的结构，尽管括号嵌套可能十分复杂，但是这种架构只是遍历了一遍输入的表达式的结构层次，并频繁使用数学表达式中的加法、乘法方法，来最终计算出不含括号的数学表达式。因此，这种架构并没有显示地表示出拆括号的步骤，只是对“输入的表达式”和“数学表达式”两个类型进行了建模，并提供了两种类型间的转换方法。

这种架构依赖于：

1. 输入表达式可能有多层嵌套，但相邻的层次间的逻辑关系简单（每个表达式都是若干个项的和，每个项都是若干因子的积）
2. 计算的最终结果可以有一致的结构

这种架构的缺点在于，难以进行三角优化。由于数学表达式使用了两层HashMap嵌套进行储存，系数与指数分布在两个不同的类间，这给三角优化带来了很大的困难。这也说明了，MathExpre和NormalTerm间的耦合程度过高，亟待解耦或合并。

其他架构的讨论

在阅读其他同学架构时，我看到有些同学将表达式、项、各种因子均统一实现一个名为Factor的接口，基本形式如下：

|- Factor(Interface)
  |- ExpreFactor
  |- Term
  |- ConstFactor
  |- TriFunct
  |- PowerFunct

这种架构的好处是，将所有的层次都视为“因子”的一个子层次。这是合理的，因为表达式本来就是一个嵌套的概念，逻辑依赖关系形成了一个环，在这种架构中只是将“因子”这一直接依赖关系最多的层次作为了顶层。例如：

• 表达式可以认为是一个系数为1的表达式因子
• 项可以认为是一个表达式，而表达式可以认为是表达式银子

在这种层次中，由于设计了Factor这一公共接口，使大部分方法的返回值都可以upcast到Factor。

我认为，这种架构的缺点在于，与人类的认知相违背。虽然我们思考后认同表达式是因子的一种，但从真实世界的一般认知来看，仍然是表达式“统揽”其他结构比较通顺。由于面向对象程序设计的优势之一便是，可以直接站在真实世界的角度进行编程，而不需要程序员先将真实世界映射到程序后再进行编程，因此我认为，类的架构与真实世界中合理、通顺的结构相符是十分重要的一点。

架构的迭代

在第一次作业中，由于没有三角函数、自定义函数和求和函数，最终表达式一定是一个多项式。在这次作业中，mathexpression包内只实现了多项式的若干类，实现了加法乘法方法。

第二次作业中，由于增加了这些函数，因此对sentence包进行了大规模扩展，但已有的架构仍然保留：sentence包按输入的层次对输入表达式进行分层存储，mathexpression储存数学表达式。由于此时结果不是多项式，因此花了很长的时间思考mathexpression中对最终结果范式的设计，以及重构。

第三次作业主要支持嵌套，由于我的设计中自然满足了嵌套规则，因此没有进行大规模修改，只是解决了一些小问题，例如输出的sin(-x)不符合形式化定义。

总的来说，由于一开始的架构较为合理，所以三次迭代都较为顺利，没有大规模的推翻重构。

程序结构分析

第一次作业

代码规模

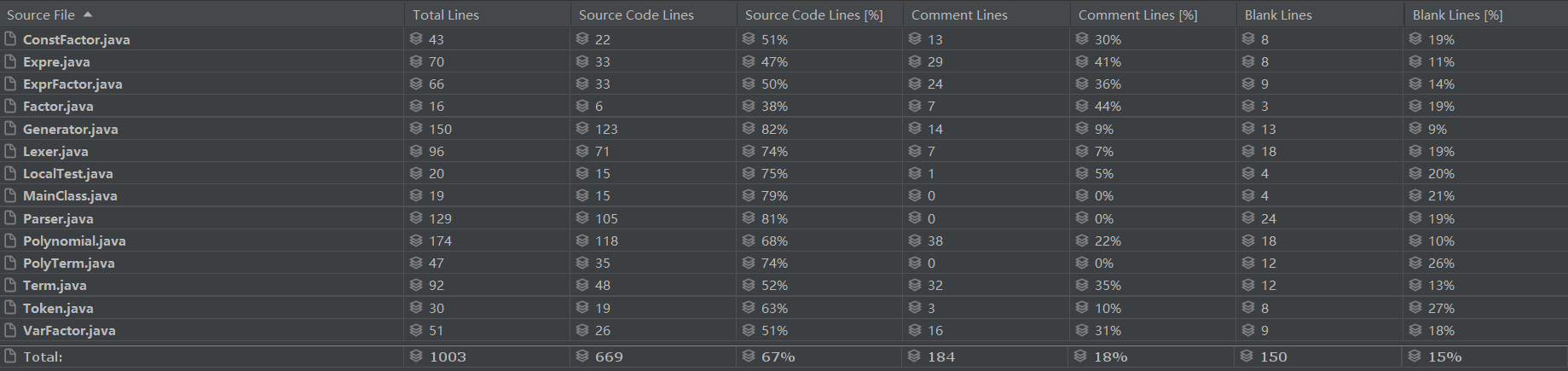
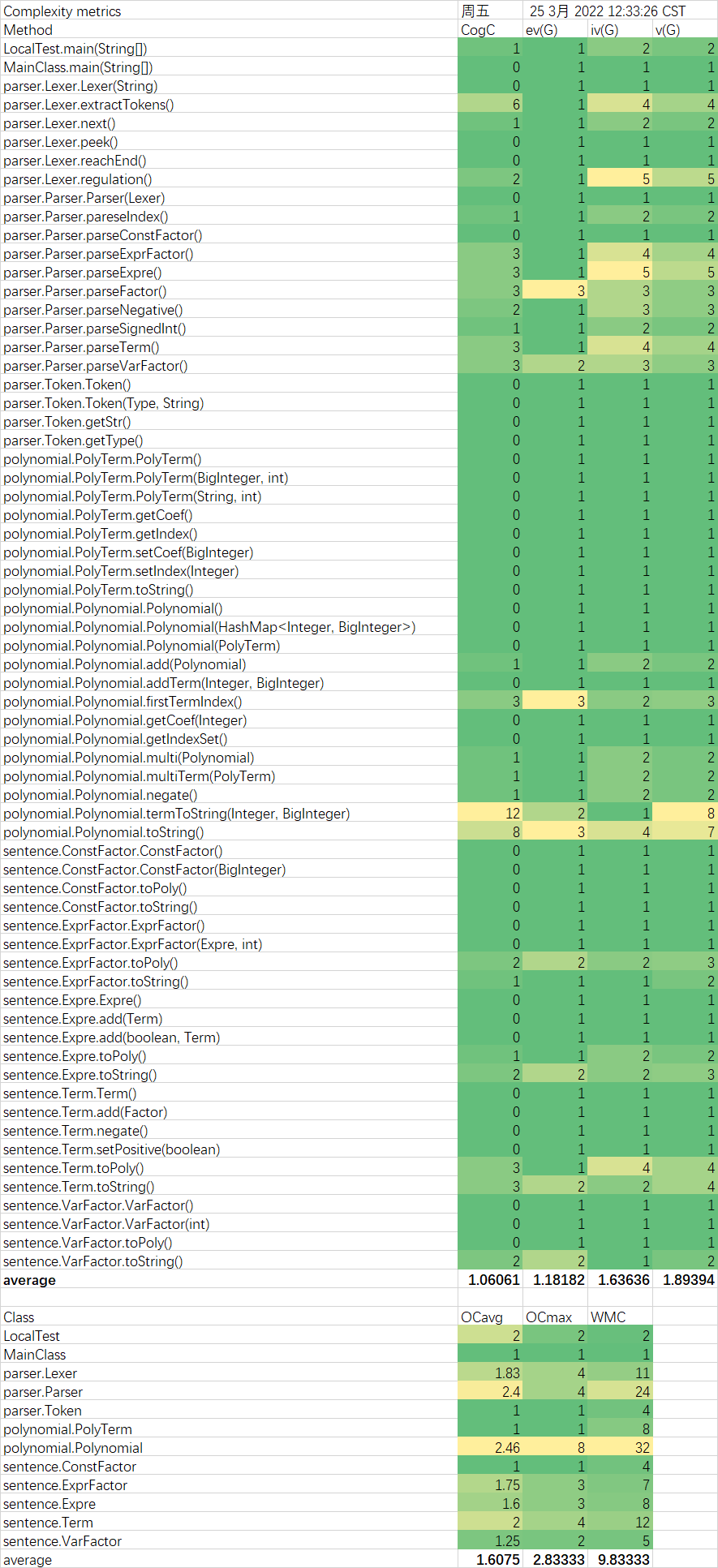
复杂度分析

第二次作业

代码规模

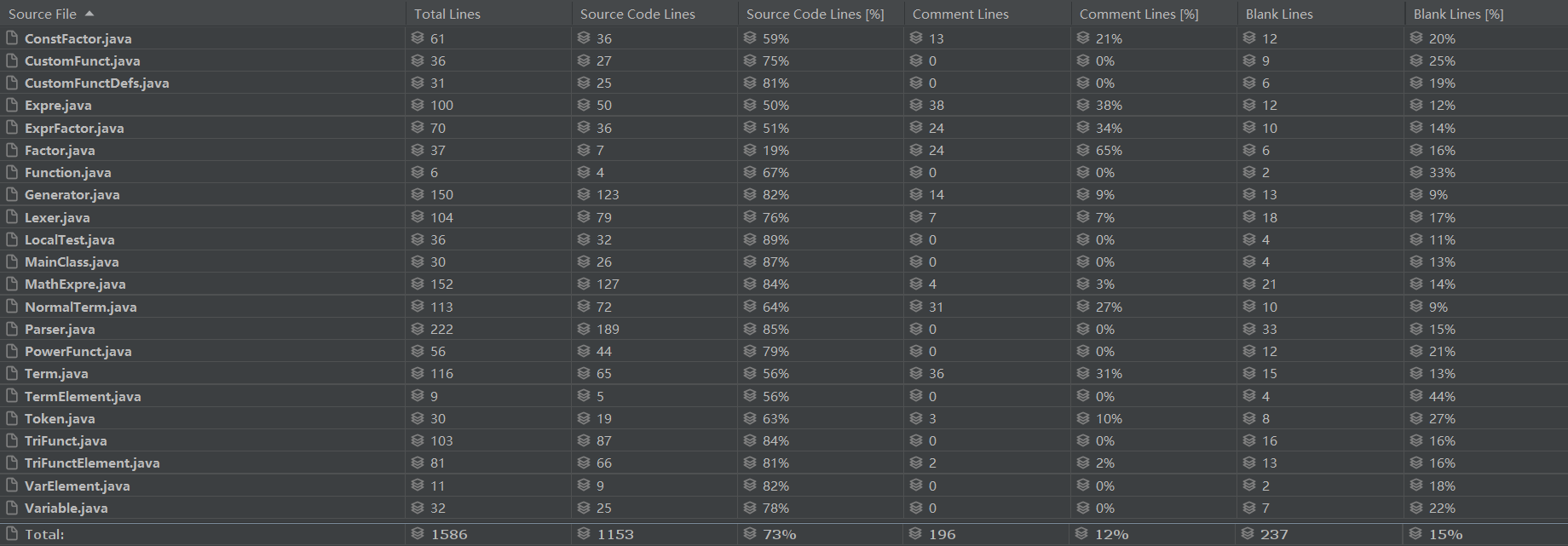
复杂度分析

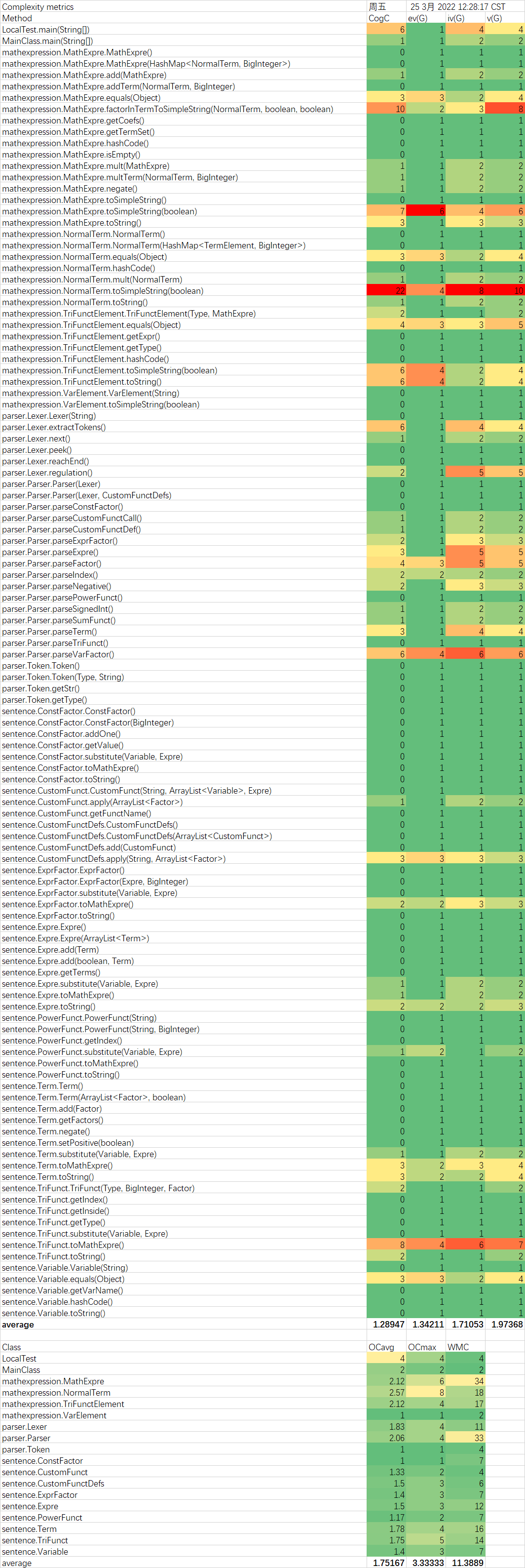
第三次作业

代码规模

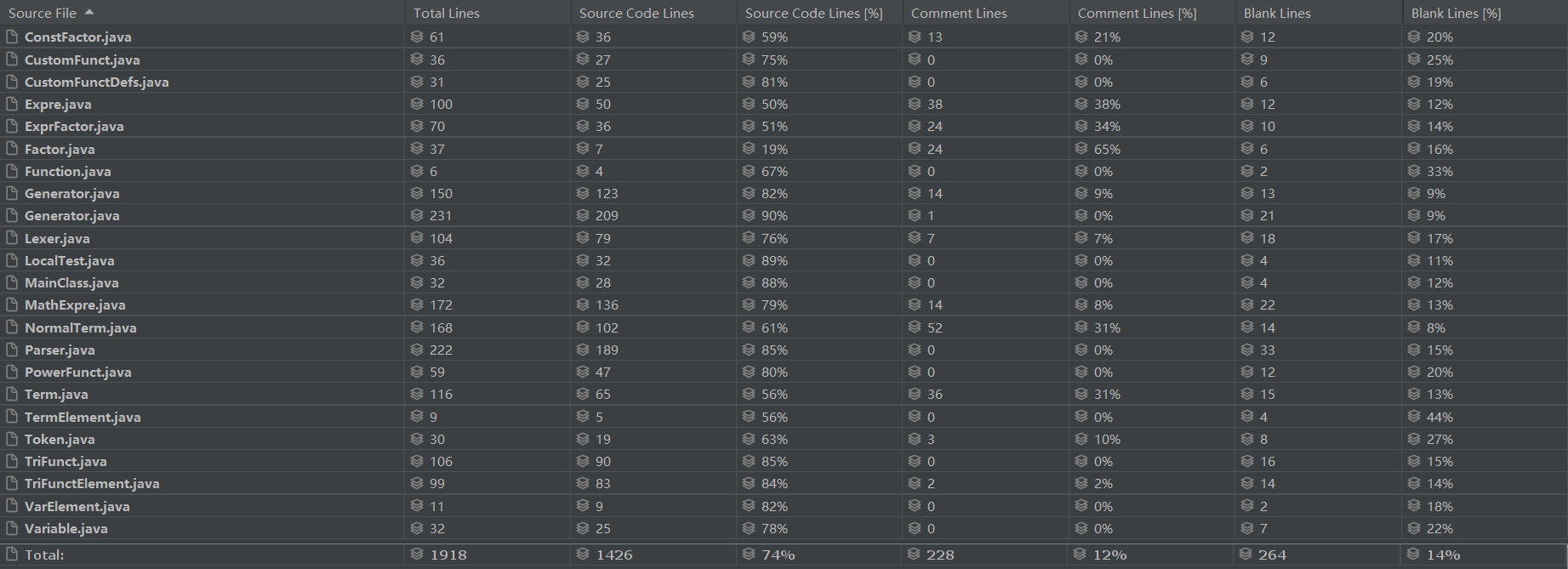
复杂度分析

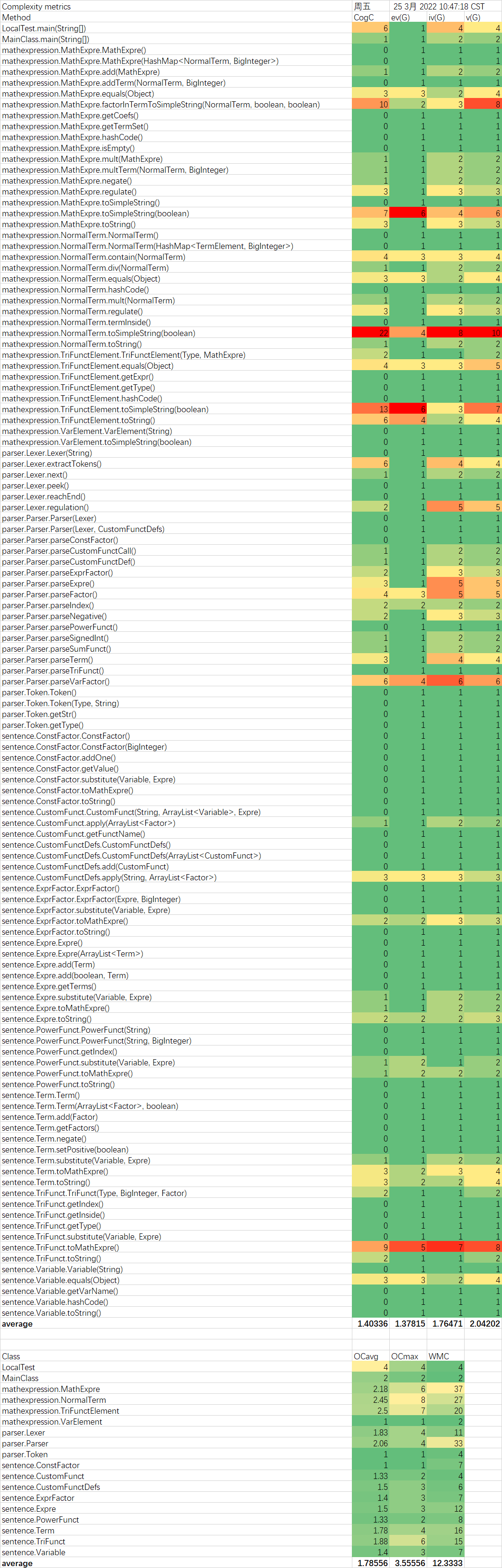
在三次作业中，复杂度较高的大部分是转换为字符串的函数。这说明在转换为字符串的过程中，代码比较冗长，判断较多，没有很好的模块化设计。在调试过程中，出现问题最多的也是这些复杂度较高转换字符串的函数。这说明，出现bug的概率和复杂度呈正相关，因此我们需要尽量降低bug。

另外，在本次的面向对象程序设计中，我体会到了方法的简短、低复杂度对代码正确性的贡献。看似十分复杂的操作，拆分成各个类的不同小方法，每个方法都很短，而最后的测试往往不会发现太多的问题。像是转换字符串这种看似简单的操作，没有拆分成不同方法，放在同一个方法中实现，导致该方法复杂度较高，反而出现了更多的bug。

静态分析

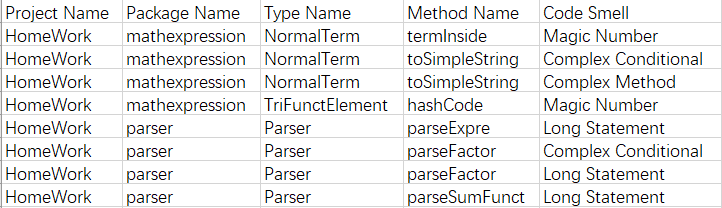
测试与bug

测试的样例主要包括随即生成和手工构造两种。对于随机生成，可直接根据形式化描述进行生成，这是parse的逆过程。需要注意的是，在随机生成的过程中，需要注意边界的控制，否则将无法对生成的表达式的复杂度进行控制。

在强测和互侧中没有被发现bug。

互侧中，我大部分使用了黑盒测试的方法，用自己构造和生成的数据测试他人的程序，发现问题后，再去读他人的代码，分析错误之处。

下面列出在测试中发现的几个有趣的问题。

范式不唯一

对于一些特殊的数学表达式，它们可能拥有不同的范式。

例如，\(x\)的表达方法有：

\[1 * x^1 \\ 1 * x^1 * sin^0(x^333333)\\ 1 * x^1 * cos^0(x^0) \\ 1 * x^1 * sin^0(x) * cos^0(x) * sin^0(x^2) * cos^0(x^2) * sin^0(x^3) * cos^0(x^3) \]

虽然这不会导致错误，但会给合并同类项带来很大的困难。由于我们是直接将因子放入HashMap，因此冗余项的出现会导致数学意义上相等，但HashMap不合并的现象出现。我们将输入表达式中的所有因素都化为统一的范式的原因之一，便是为了方便合并。因此，我们必须要额外实现一些内容，从而使所有的数学表达式都有着唯一的表示法。

因此，在mathexpression包中，大部分类都实现了regulate方法。该方法将所有0次方的项删除。

变量名冲突

在处理自定义函数和求和函数时，我对sentence包中的所有类实现了substitute方法，用于将一个变量替换为给定的Factor。对于求和函数，则将自变量i替换成特定的ConstFactor，之后将替换得到的表达式相加。对于自定义函数，我的处理方法如下：

public Expre apply(ArrayList<Factor> tars) {
    Expre ans = definition;
    for (int i = 0; i < vars.size(); ++i) {
        ArrayList<Term> terms = new ArrayList<>();
        ArrayList<Factor> factors = new ArrayList<>();
        factors.add(tars.get(i));
        terms.add(new Term(factors, true));
        Expre target = new Expre(terms);
        ans = ans.substitute(vars.get(i), target);
    }
    return ans;
}

这是在函数中依次循环每个变量，将变量替换成相应Factor。由于没有特殊处理自定义函数的变量名，因此会导致新替换的变量内部的自变量被再次替换的问题。考虑一下数据：

1
f(y, x) = y + x
f(x**2, x**5)

若先替换自定义函数中的变量\(y\)，替换后式子变为x**2 + x。下一步使将x替换为x**5，表达式会被替换为x**10 + x**5。

因此，对于输入的数据，需要先对代替换的变量进行标记（或者先改名），之后再进行上述的替换。

可变对象

由于所有对象均使用引用来访问，因此若一个对象发生了变化，指向它的引用所对应的对象也都发生改变（其实是一个对象）。这会导致很多问题，因此在作业中使用了不可变对象。

然而，我没有重写clone方法，而是以笨拙的重构HashMap的方法来保证对象的不可变。在以后的作业中可以改进。

心得体会

在这次作业中，我最深刻的体会就是理解了面向对象程序设计的优势，在此谈谈我的理解。

面向对象程序设计的优势之一便是，程序员可以不站在计算机的角度进行编程，而直接站在真实世界的角度进行编程。程序都是为了解决真实世界问题的，而真实世界往往会非常复杂。对于一些面向过程的语言来说，程序员必须先建立真实世界和程序间的映射关系，之后站在计算机的角度进行编程。编程时，程序员需要对真实世界中的问题给出全面、健壮的流程，一步一步按照机械化的判断、跳转等流程执行下去，需要程序员转换思维方式。

举个例子来说，人们如果想要把一些东西放入冰箱，一般来说都不会去思考将物品放入冰箱的流程，而是会直接进行这个动作。但是对于程序员来说，将物品放入冰箱的流程需要被抽象成规定的几个流程：

1. 打开冰箱门
2. 观察冰箱内部第一层
3. 判断该层是否有空余位置
   • 若有，则转到4
   • 否则，观察冰箱的下一层，转到3
4. 将物品放入该层
5. 关闭冰箱门

上述流程是普通的冰箱用户不会思考的。由此可以看出，计算机的视角与真实世界的视角（人类的视角）是有较大的偏差的。

另外，真实世界中的问题远不止将物品放入冰箱这个例子这么简单。大部分真实世界中的问题进行流程化的抽象都是非常困难的。因此，面向对象程序设计中，程序员摆脱了这个计算机视角和真实世界视角间转换的环节，我认为这是至关重要的一点。在使用面向对象思想进行编程时，程序员所做的工作便是有条理地，像是讲故事一样，把真实世界描述出来。

如果不使用面向对象的思想完成本单元作业，那么编程的首要问题便是选取合适的数据结构对表达式进行储存。由于含有嵌套的层次结构，数据结构的选择和使用上可能会有一些困难。在面向对象的程序设计中，具体的数据结构等对程序员保持了一定程度上的透明，虽然也有一些与数据结构紧密相关的容器，但是在很多情况下，特别是这次的层次化建模作业中，我们完全无需考虑使用类似“树”的结构进行存储和操作。

因此，我在本次作业中，也严格地在真实世界上进行层次化建模。我对输入的表达式单独构造了一个包，对计算后的数学表达式又单独构造了一个包，看似重复，但实则是为了使程序与真实世界中的人类视角一致。