母函数入门

BZOJ3027

http://www.lydsy.com/JudgeOnline/problem.php?id=3027

显而易见

母函数是这坨玩意

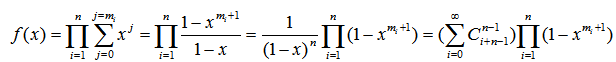
 所以总数不超过b的方案，对于这一坨

 我们暴力枚举一个kx^y

那么它对ans的贡献为

 

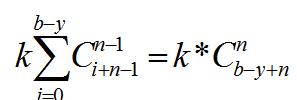
复杂度O（2ⁿ*n） 

#include<cstdio>
#define FOR(i,s,t) for(register int i=s;i<=t;++i)
typedef long long ll;
int mul;
const int mod=2004;
int n,a,b;
int m[12];
inline int getC(int n,int m){
	if(n<m)return 0;
	ll Mod=1ll*mul*mod,ans=1ll;
	for(register int i=n-m+1;i<=n;++i)ans=1ll*ans%Mod*i%Mod;
	return (ans/mul)%mod; 
}
inline int dfs(int dep,int k,int y,int lim){
	return (dep==n+1?(mod+k*getC(n+lim-y,n)%mod):(dfs(dep+1,-k,y+m[dep]+1,lim)+dfs(dep+1,k,y,lim)))%mod;
}
int main(){
	scanf("%d%d%d",&n,&a,&b);
	mul=1;FOR(i,1,n)mul*=i,scanf("%d",m+i);
	printf("%d\n",(dfs(1,1,0,b)-dfs(1,1,0,a-1)+mod)%mod);
	return 0;
} 

　　

BZOJ3028

http://www.lydsy.com/JudgeOnline/problem.php?id=3028

(1).

(2).

(3).

(4).

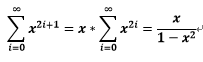
(5).

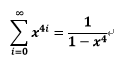
(6).

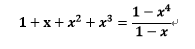
(7).

(8).

 

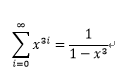
把(1)~(8)乘起来得到 

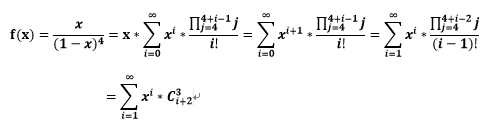
因此，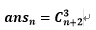

#include<cstdio>
char c;
const int mod=10007;
inline int fp(int a,int b){
	int ret=1;
	while(b){
		if(b&1)ret=ret*a%mod;
		b>>=1;
		a=a*a%mod; 
	}
	return ret;
}
int data;
int main(){
	while(c=getchar(),c<='9'&&c>='0')data=(data<<1)+(data<<3)+c-48,data%=mod;
	printf("%lld",1ll*data*(data+1)%mod*(data+2)%mod*fp(6,mod-2)%mod);
    return 0;  
}