图总结

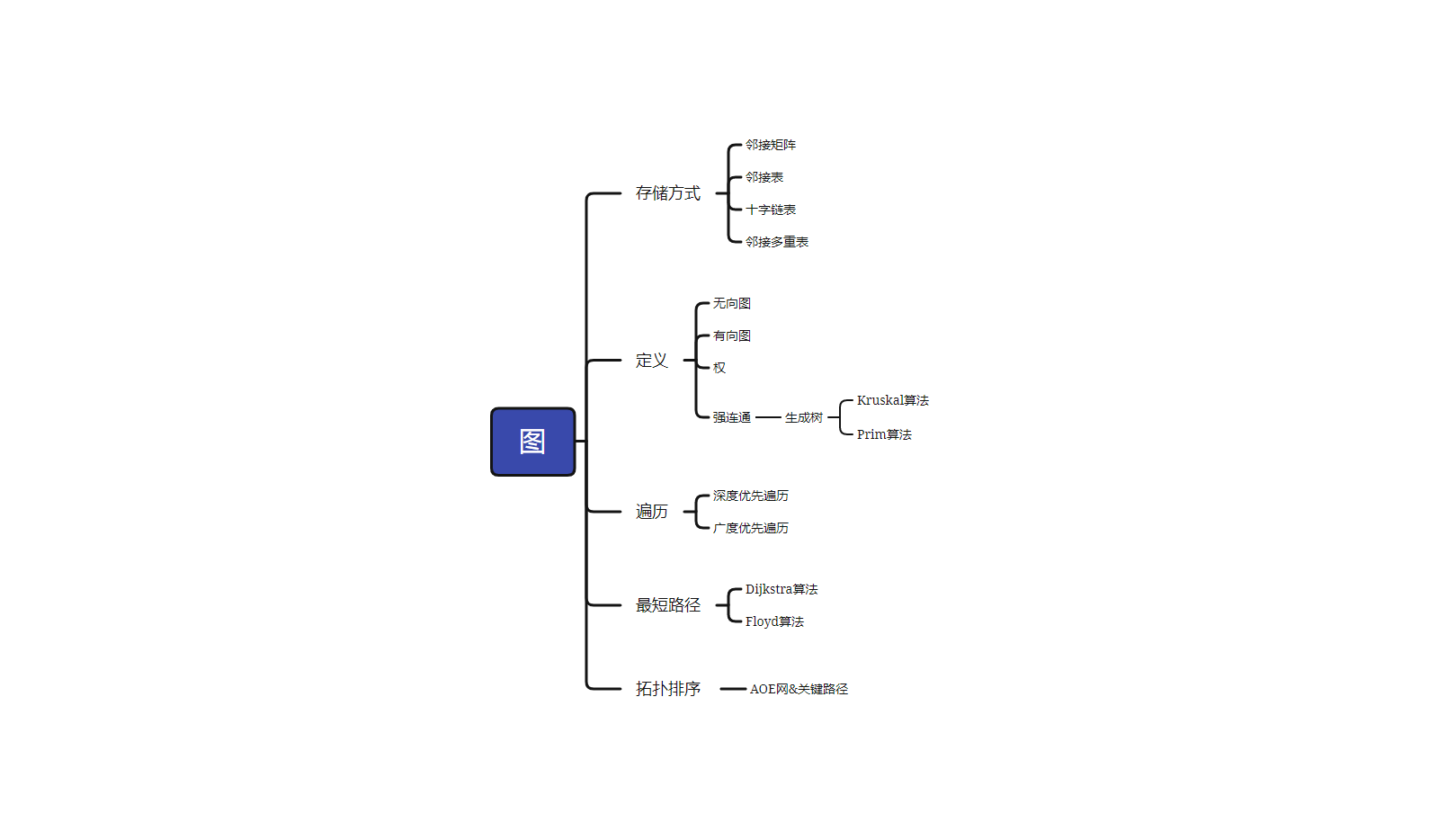
1.思维导图

2.笔记

Dijkstra算法

要求：边权非负

思路：顶点分为两组，一旦确定了某点的最短路径就放入第一组，其余归为第二组；每次取能够到的最短的那条路径。

具体实现：每次加入第一个组时更新第二组的距离值，选取距离值最小的顶点加入第一组

设置length数组和pre数组

复杂度：没有最小堆：O(V2+E)，最小堆不删除旧值：O((|V|+|E|)log|E|)

Floyd算法

要求：允许边权值为负

每次算出从某点到某点中间顶点序号不大于K的最短路径长度，n次以后包括了所有最终的最短路径。

设置path数组（初始-1）和adj数组

复杂度：O(n3)

Prim算法

思路：贪心

从任意一点开始，把这个点包括在MST里，对一个点在MST中而另一个不在的边取出最小的放进MST

复杂度同Dijkstra

Kruskal算法

将所有边分成很多等价类，连通后就成为同一个等价类，按权值大小顺序处理每一条边，该边连接不同等价类就加到MST

复杂度O(|E|log|E|)（堆排序时间）

拓扑排序

不唯一

基本思想，判断环路（bfs和dfs，dfs不能判断环）

复杂度：相邻矩阵O(|V|3)，邻接表：O(2|V|+|E|)

Dfs

邻接表代价有向图O(|V|+|E|) 无向图O(|V|+2|E|) 相邻矩阵O(|V|2)

BFS

复杂度与dfs相同

3.代码

题目：7-2 六度空间

解答代码:

#include <windows.h>
#include<iostream>
#include<queue>
using namespace std;
#define max 1001
int  n, m;
int a[1001][1001] = { 0 };
int vis[1001] = { 0 };
int bfs(int x)
{
	memset(vis, 0, sizeof(vis));
	int t = 0, cnt = 1;
	queue<int>q;
	vis[x] = 1;
	q.push(x);
	int k = 1;
	while (!q.empty())
	{
		int v = 0;
		for (int j = 1; j <= k; j++)
		{
			int temp = q.front();
			q.pop();
			for (int i = 1; i <= n; i++)
			{
				if (!vis[i] && a[temp][i])
				{
					vis[i] = 1;
					q.push(i);
					cnt++;
					v++;
				}
			}
		}
		k = v;
		t++;
		if (t == 6)
			break;
	}
	return cnt;
}
int main()
{
	cin >> n >> m;
	for (int i = 1; i <= m; i++)
	{
		int b, c;
		cin >> b >> c;
		a[b][c] = a[c][b] = 1;
	}
	for (int i = 1; i <= n; i++)
	{
		cout << i << ": ";
		printf("%.2lf", bfs(i) * 100.0 / n);
		cout << "%" << endl;
	}
}

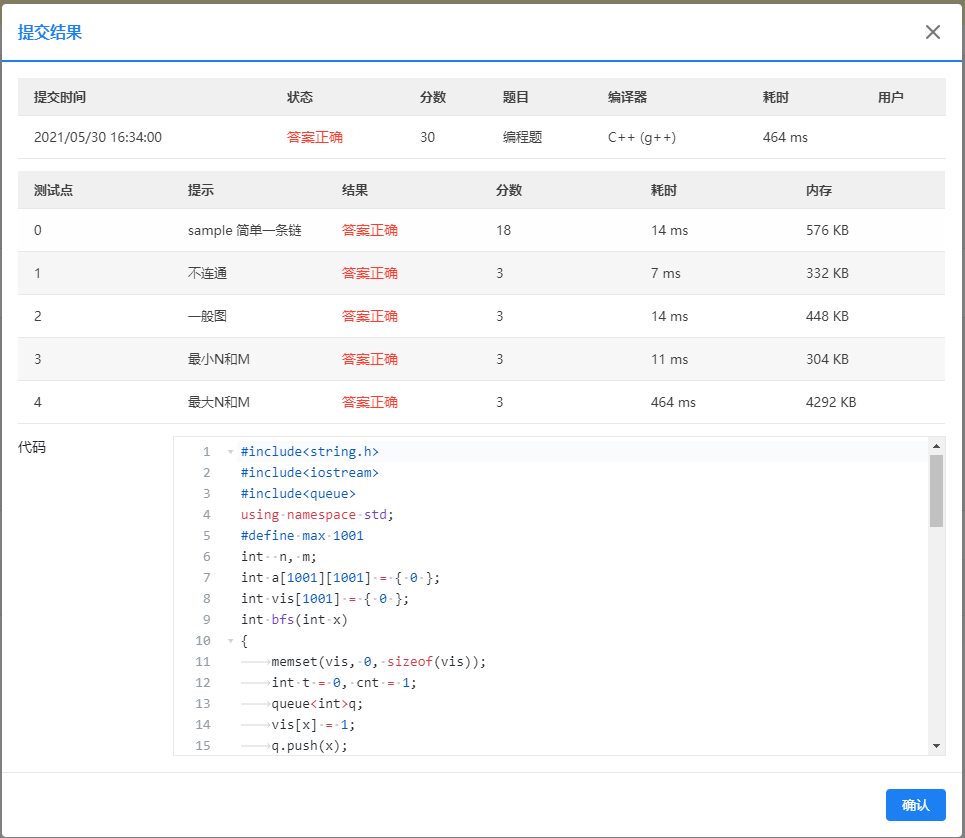
结果: