树，二叉树，查找算法总结

# 1.思维导图

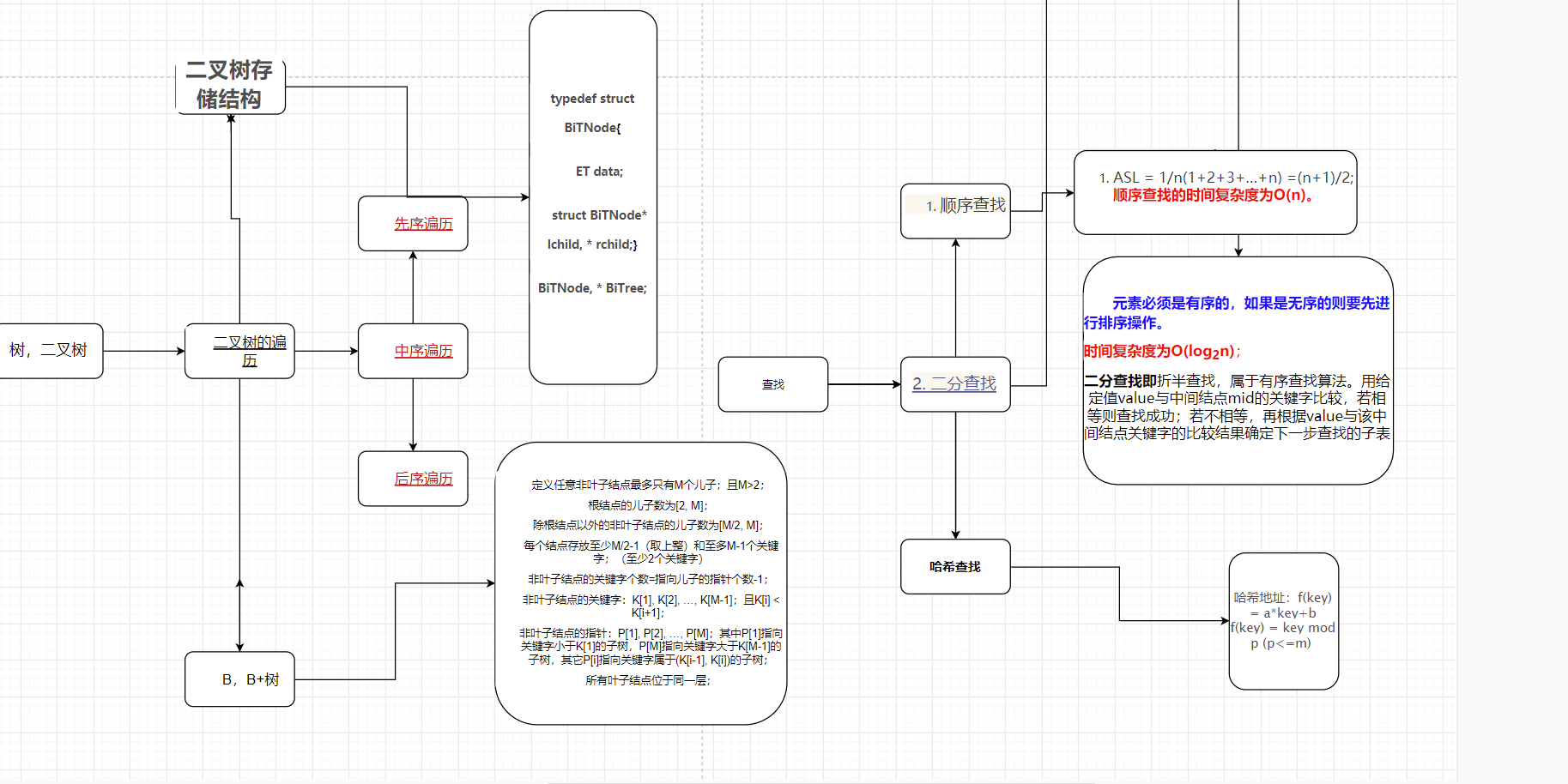
# 2.笔记

1.一般树的存储：

1.双亲表示法：求父节点方便。
2.孩子表示法：求子节点方便。
3.双亲孩子表示法：求父节点和子节点都很方便。
4.二叉树表示法：将一颗普通树转化为二叉树。

2.二叉树的性质：

1.在二叉树的第i层上至多有2^(i-1)个结点（i>0）。
2.深度为k的二叉树至多有2^k-1个结点（k>0）。
3.对于任意一棵二叉树，如果其叶结点为N0，而度数为2的结点总数为N2，则N0=N2+1。
4.具有n个结点的完全二叉树的深度必为 log（2n）+1。
5.对完全二叉树，若从上至下、从左只右编号，则编号为i的节点，其左孩子编号必为2i，其有孩子编号必为2i+1；其双亲的编号必为i/2（i=1时为根 除外）。

3.折半查找的时间复杂度为：O(log2n)。

4.B树：

1、概念：
它或者是一棵空树；或者是具有下列性质的二叉树：
(1)若左子树不空，则左子树上所有结点的值均小于左子树所在树的根结点的值；
(2)若右子树不空，则右子树上所有结点的值均大于右子树所在树的根结点的值；
(3)左、右子树也分别为二叉排序树；
2、B树的查找：
时间复杂度与树的深度的有关。
步骤：若根结点的关键字值等于查找的关键字，成功。
否则：若小于根结点的关键字值，递归查左子树。
若大于根结点的关键字值，递归查右子树。
若子树为空，查找不成功。
3、B树的插入：
首先执行查找算法，找出被插结点的父亲结点。
判断被插结点是其父亲结点的左儿子还是右儿子。将被插结点作为叶子结点插入。
若二叉树为空。则首先单独生成根结点。
注意：新插入的结点总是叶子结点，所以算法复杂度是O(h)。
（1）.如果删除的结点没有孩子，则删除后算法结束；
（2）.如果删除的结点只有一个孩子，则删除后该孩子取代被删除结点的位置；
（3）.如果删除的结点有两个孩子，则选择该结点的后继结点（该结点右孩子为根的树中的左子树中的值最小的点）或者前驱节点（该结点左孩子为根的树中的右子树中值最大的点）作为新的根，同时在该后继结点或者前驱节点开始，执行前两种删除算法，删除算法结束。

5.B+树：

一棵m阶的B+树满足下列条件：
（1）每个结点最多m个孩子。
（2）除根结点和叶子结点外，其它每个结点至少有m/2(取上限)个孩子。
（3）根结点至少有两个孩子。
（4）所有的叶子结点在同一层，且包含了所有关键字信息。
（5）有k个孩子的分支结点包含k个关键字。

3.疑难问题及解决方案

## 题目:
1.编写SearchBST(T,KEY)与InsertBST(T,key)的伪代码,并实现。
2.编写CreateBST（T）的伪代码实现从控制台输入创建BST树。最后使用代码实现。使用"50 30 80 20 40 90 10 25 35 85 23 88”创建BST，并中序输出该BST。
## 思路
1,2题较为简单直接进行代码展示与结果展示（搜索按照二叉排序树的定义直到搜索为空即可，插入树为空则建树，若不为空则用定义找到节点，按定义插入，建树读入数据用插入函数建树）.
## 代码
### 查找
```
BiTree SearchBST(BiTree t, ET k)
{
if(t==NULL)
return NULL;
if(t->data == k)
{
return t;
}
else if (k<t->data)
SearchBST(t->lchild, k);
else if(k>t->data)
SearchBST(t->rchild, k);
}
```
### 插入
```
bool InsertBST(BiTree& T, ET k)
{
if(T == NULL)
{
T = new BiTNode;
T->data = k;
T->lchild = NULL;
T->rchild = NULL;
return true;
}
else if(T->data>k)
InsertBST(T->lchild, k);
else if(k > T->data)
InsertBST(T->rchild,k);
}
```
### 创建
```
void CreateBST(BiTree& T)
{
int n;
cin >> n;
while (n != -1)
{
InsertBST(T, n);
cin >> n;
}
}
```
### 输出结果
[](http://111.230.235.113/wordpress/wp-content/uploads/2021/04/bst1.png)
## 题目
3.编写DeleteBST(k,key)的伪代码实现从T中删除关键字key。如果无法编写出来,请写出在BST中删除关键字所需注意的事项。
4.使用代码实现DeleteBST(T,key)
### 思路
我们将删除节点的节点情况分为三种情况讨论.
1.删除的节点为根节点。
2.删除的节点只有左/右节点。
3.删除的节点拥有两个节点。
对于有两个节点的根节点可视为等同于情况3而只含一个分支的根节点则放在情况二中先判断在讨论二节点。对于二节点直接上图说明。
[](http://111.230.235.113/wordpress/wp-content/uploads/2021/04/bst2.png)
如图只需要删除该节点后将该节点的子节点接到删除节点的父母节点即可
而情况3较为复杂,也上图说明。
[](http://111.230.235.113/wordpress/wp-content/uploads/2021/04/bst3.png)
我们找到要删除节点的右子树的最小节点（即最左节点与删除节点进行替换就行了）
### 代码
```
bool DeleteBST(BiTree& t, ET k)
{
if (t == NULL)
return false;
BiTree n=t , p=NULL ;
while (n)
{
if (k == n->data)
break;
else if (k < n->data)
{
p = n;
n = n->lchild;
}
else
{
p = n;
n = n->rchild;
}
}
if (n == NULL)
return false;
if (n->lchild == NULL)
{
if (n == t)
t = n->rchild;
else
{
if (n == p->lchild)
{
p->lchild = n->rchild;
}
else
{
p->rchild = n->rchild;
}
}
return true;
}

else if (n->rchild == NULL)
{
if (n == t)
t = n->lchild;
else
{
if (n == p->rchild)
{
p->rchild = n->lchild;
}
else
{
p->lchild = n->lchild;
}
}
return true;
}

else
{
if (n->lchild != NULL && n->rchild != NULL)
{
BiTree r = n->rchild;
p = n;
while (r->lchild)
{
p = r;
r = r->lchild;
}
n->data = r->data;
if (r == p->lchild)
p->lchild = r->rchild;
else
p->rchild = r->rchild;
delete r;
r = NULL;
}
return true;
}
return false;
}
```
### 运行结果
[](http://111.230.235.113/wordpress/wp-content/uploads/2021/04/bst4.png)
## 题目
5.随机生成包含100000个节点的BST，节点的值为整数其范围为[-300000,300000]，输出其树的高度。然后随机搜1000个数值，统计平均每次的查找长度。
### 思路
这题的思路其实很简单，我们对题目进行分块解读。任务1:随机生成树，与普通生成树的代码相同，只要通过rand（）函数进行输入数据即可。任务2.输出树的高度:过于基础，不论述，随机搜，同样通过rand()函数生成数据读入，统计平均每次的查找长度，只要略微改动查找数的代码即可:创建一个累加器每向下一层就+1，找到，则返回此时的累加数，未找到则累加数+1.将1000个累加数加起来/1000即可获得平局每次查找长度.
### 代码
```
void CreateRandBST(BiTree& T)
{
int t = 0;
int n;
n= rand() * 10 % 300000 - 150000;
while (t<100000)
{
InsertBST(T, n);
n = rand() * 10 % 300000 - 150000;
t++;
}
}
```
```
int h(BiTree t)
{
if (!t)
return 0;
int n = 0;
int lh = h(t->lchild);
int rh = h(t->rchild);
if (lh > rh)
n = lh;
if (rh > lh)
n = rh;
if (lh == rh)
n = lh;
return n + 1;
}
```
```
BiTree ASL(BiTree t,ET k,int &cnt)
{
if (t == NULL || t->data == k)
{
if (t != NULL)
cnt++;
return t;
}
if (k < t->data)
{
cnt++;
return ASL(t->lchild, k, cnt);
}
else
{
cnt++;
return ASL(t->rchild, k, cnt);
}
}
```
### 运行结果
[](http://111.230.235.113/wordpress/wp-content/uploads/2021/04/bst5.png)
## 总代码
```
#include <stdio.h>
#include <windows.h>
#include<iostream>
using namespace std;
typedef int ET;
typedef struct BiTNode
{
ET data;
struct BiTNode* lchild, * rchild;
}
BiTNode, * BiTree;
BiTree SearchBST(BiTree t, ET k)
{
if (t == NULL)
return NULL;
if (t->data == k)
{
return t;
}
else if (k < t->data)
SearchBST(t->lchild, k);
else if (k > t->data)
SearchBST(t->rchild, k);
}
bool InsertBST(BiTree& T, ET k)
{
if (T == NULL)
{
T = new BiTNode;
T->data = k;
T->lchild = NULL;
T->rchild = NULL;
return true;
}
else if (T->data > k)
InsertBST(T->lchild, k);
else if (k > T->data)
InsertBST(T->rchild, k);
}
void CreateBST(BiTree& T)
{
int n;
cin >> n;
while (n != -1)
{
InsertBST(T, n);
cin >> n;
}
}
void CreateRandBST(BiTree& T)
{
int t = 0;
int n;
n = rand() * 10 % 300000 - 150000;
while (t < 100000)
{
InsertBST(T, n);
n = rand() * 10 % 300000 - 150000;
t++;
}
}
void zx(BiTree t)
{
if (t != NULL)
{
zx(t->lchild);
cout << t->data << " ";
zx(t->rchild);
}
}
bool DeleteBST(BiTree& t, ET k)
{
if (t == NULL)
return false;
BiTree n=t , p=NULL ;
while (n)
{
if (k == n->data)
break;
else if (k < n->data)
{
p = n;
n = n->lchild;
}
else
{
p = n;
n = n->rchild;
}
}
if (n == NULL)
return false;
if (n->lchild == NULL)
{
if (n == t)
t = n->rchild;
else
{
if (n == p->lchild)
{
p->lchild = n->rchild;
}
else
{
p->rchild = n->rchild;
}
}
return true;
}

else if (n->rchild == NULL)
{
if (n == t)
t = n->lchild;
else
{
if (n == p->rchild)
{
p->rchild = n->lchild;
}
else
{
p->lchild = n->lchild;
}
}
return true;
}

else
{
if (n->lchild != NULL && n->rchild != NULL)
{
BiTree r = n->rchild;
p = n;
while (r->lchild)
{
p = r;
r = r->lchild;
}
n->data = r->data;
if (r == p->lchild)
p->lchild = r->rchild;
else
p->rchild = r->rchild;
delete r;
r = NULL;
}
return true;
}
return false;
}
int h(BiTree t)
{
if (!t)
return 0;
int n = 0;
int lh = h(t->lchild);
int rh = h(t->rchild);
if (lh > rh)
n = lh;
if (rh > lh)
n = rh;
if (lh == rh)
n = lh;
return n + 1;
}
BiTree ASL(BiTree t, ET k, int& cnt)
{
if (t == NULL || t->data == k)
{
if (t != NULL)
cnt++;
return t;
}
if (k < t->data)
{
cnt++;
return ASL(t->lchild, k, cnt);
}
else
{
cnt++;
return ASL(t->rchild, k, cnt);
}
}
int main()
{
int n, a;
BiTree t;
t = new BiTNode;
t = NULL;
CreateBST(t);
zx(t);
cout << "\n";
cout << "cin search number\n";
cin >> n;
if (SearchBST(t, n) == NULL)
cout << "no find\n";
else
cout << "FIND\n";
cout << "cin delete number\n";
cin >> a;
if (DeleteBST(t, a) == 1)
cout << "delete success\n";
else
cout << "tree is NULL or the number is not in the tree\n";
zx(t);
system("pause");
int sum = 0, b, cnt;
BiTree T;
T = new BiTNode;
T = NULL;
CreateRandBST(T);
cout << h(T) << endl;
for (int i = 0; i < 1000; i++)
{
b = rand() * 10 % 300000 - 150000;
cnt = 0;
ASL(T, b, cnt);
sum = sum + cnt;
}
cout << "ASL:";
cout << sum / 1000;
return 0;
}
```
### 运行结果
[](http://111.230.235.113/wordpress/wp-content/uploads/2021/04/bst6.png)
## 更新使用Easyx画出二叉树
```
#include <graphics.h>
#include <stdio.h>
#include <windows.h>
#include<iostream>
using namespace std;
typedef int ET;
typedef struct BiTNode
{
ET data;
struct BiTNode* lchild, * rchild;
}
BiTNode, * BiTree;
void Paint(BiTree BT, int x, int y, int g)
{
char c[3];
int right = 0, left = 0;
if (BT)
{
setcolor(WHITE);
circle(x, y, 10);
//将相应数字转化为字符
c[0] = BT->data / 10 + 48;
c[1] = BT->data % 10 + 48;
c[2] = '\0';
outtextxy(x - 7, y - 6, c);
Sleep(1);
if (BT->lchild != NULL)
{
if (x > g) left = (x - g) / 2 + g;
if (x < g) left = (x - g) / 2 + x;
line(x - 3, y, left, y + 50);
}
if (BT->rchild != NULL)
{
if (BT->lchild != NULL)right = 2 * x - left;
else
{
if (x < g) right = (x + g) / 2;
else right = x + 40;
}
line(x + 3, y, right, y + 50);
}
Paint(BT->lchild, left, y + 50, x);
Paint(BT->rchild, right, y + 50, x);
}
}
BiTree SearchBST(BiTree t, ET k)
{
if (t == NULL)
return NULL;
if (t->data == k)
{
return t;
}
else if (k < t->data)
SearchBST(t->lchild, k);
else if (k > t->data)
SearchBST(t->rchild, k);
}
bool InsertBST(BiTree& T, ET k)
{
if (T == NULL)
{
T = new BiTNode;
T->data = k;
T->lchild = NULL;
T->rchild = NULL;
return true;
}
else if (T->data > k)
InsertBST(T->lchild, k);
else if (k > T->data)
InsertBST(T->rchild, k);
}
void CreateBST(BiTree& T)
{
int n;
cin >> n;
while (n != -1)
{
InsertBST(T, n);
cin >> n;
}
}
void CreateRandBST(BiTree& T)
{
int t = 0;
int n;
n = rand() * 10 % 300000 - 150000;
while (t < 100000)
{
InsertBST(T, n);
n = rand() * 10 % 300000 - 150000;
t++;
}
}
void zx(BiTree t)
{
if (t != NULL)
{
zx(t->lchild);
cout << t->data << " ";
zx(t->rchild);
}
}
bool DeleteBST(BiTree& t, ET k)
{
if (t == NULL)
return false;
BiTree n = t, p = NULL;
while (n)
{
if (k == n->data)
break;
else if (k < n->data)
{
p = n;
n = n->lchild;
}
else
{
p = n;
n = n->rchild;
}
}
if (n == NULL)
return false;
if (n->lchild == NULL)
{
if (n == t)
t = n->rchild;
else
{
if (n == p->lchild)
{
p->lchild = n->rchild;
}
else
{
p->rchild = n->rchild;
}
}
return true;
}

else if (n->rchild == NULL)
{
if (n == t)
t = n->lchild;
else
{
if (n == p->rchild)
{
p->rchild = n->lchild;
}
else
{
p->lchild = n->lchild;
}
}
return true;
}

else
{
if (n->lchild != NULL && n->rchild != NULL)
{
BiTree r = n->rchild;
p = n;
while (r->lchild)
{
p = r;
r = r->lchild;
}
n->data = r->data;
if (r == p->lchild)
p->lchild = r->rchild;
else
p->rchild = r->rchild;
delete r;
r = NULL;
}
return true;
}
return false;
}
int h(BiTree t)
{
if (!t)
return 0;
int n = 0;
int lh = h(t->lchild);
int rh = h(t->rchild);
if (lh > rh)
n = lh;
if (rh > lh)
n = rh;
if (lh == rh)
n = lh;
return n + 1;
}
BiTree ASL(BiTree t, ET k, int& cnt)
{
if (t == NULL || t->data == k)
{
if (t != NULL)
cnt++;
return t;
}
if (k < t->data)
{
cnt++;
return ASL(t->lchild, k, cnt);
}
else
{
cnt++;
return ASL(t->rchild, k, cnt);
}
}
int main()
{
int n, a,x,y,g;
BiTree t;
x = 320, y = 30, g = 0;
t = new BiTNode;
t = NULL;
CreateBST(t);
zx(t);
initgraph(800, 550, 0);
setbkcolor(0); //设置背景颜色
cleardevice(); //清屏
Paint(t, x, y, g);
getchar();
getchar();
closegraph();
cout << "\n";
cout << "cin search number\n";
cin >> n;
if (SearchBST(t, n) == NULL)
cout << "no find\n";
else
cout << "FIND\n";
cout << "cin delete number\n";
cin >> a;
if (DeleteBST(t, a) == 1)
cout << "delete success\n";
else
cout << "tree is NULL or the number is not in the tree\n";
zx(t);
system("pause");
int sum = 0, b, cnt;
BiTree T;
T = new BiTNode;
T = NULL;
CreateRandBST(T);
cout << h(T) << endl;
for (int i = 0; i < 1000; i++)
{
b = rand() * 10 % 300000 - 150000;
cnt = 0;
ASL(T, b, cnt);
sum = sum + cnt;
}
cout << "ASL:";
cout << sum / 1000;
return 0;
}
```
## 运行结果
[](http://111.230.235.113/wordpress/wp-content/uploads/2021/04/73d8da01036f0c6f.png)