YBTOJ 6.5博弈论

A.取火柴游戏

Nim 游戏

定理：如果有 \(n\) 堆大小为 \(a_1, a_2, a_3, ..., a_n\) 的火柴
若 \(a_1 \operatorname{xor} a_2 \operatorname{xor} a_3 \operatorname{xor}...\operatorname{xor}a_n \ne 0\) 先手必胜
否则 先手必败

我们尝试证明这个结论

• 如果 \(a_1 = a_2 = a_3 = ... = a_n = 0\) 此时异或和为 0 必败

这很显然

• 如果 \(a_1 \operatorname{xor} a_2 \operatorname{xor} a_3 \operatorname{xor}...\operatorname{xor}a_n \ne 0\) 那么一定可以通过一步操作使对方面对 \(a_1 \operatorname{xor} a_2 \operatorname{xor} a_3 \operatorname{xor}...\operatorname{xor}a_n = 0\) 的局面

设这个结果为 \(k\) 则 \(k\) 的最高位一定为 \(1\)

那么一定存在一个 \(a_i\) 在对应位为 \(1\) （很显然 考虑反证）

此时一定有 \(a_i \operatorname{xor} k < k\) （因为最高位没了）

并且其它剩余 \(a\) 的异或和为 \(a_i \operatorname{xor} k\)

那么我们使 \(a_i \rightarrow a_i \operatorname{xor} k\)

就可以使对方的异或和为 \(0\)

• 如果 \(a_1 \operatorname{xor} a_2 \operatorname{xor} a_3 \operatorname{xor}...\operatorname{xor}a_n = 0\) 无论怎么操作 一定无法使对方 \(a_1 \operatorname{xor} a_2 \operatorname{xor} a_3 \operatorname{xor}...\operatorname{xor}a_n = 0\)

考虑拿出任意一个 \(a_i\) 此时剩余元素的异或和为 \(a_i\)

那么无论把 \(a_i\) 改成多少只要变小异或和一定不会为 \(0\)

以上综合起来 我们就有：

1. 如果你操作时异或和不为 \(0\) 那么一定可以让对方操作时异或和为 \(0\)
2. 如果你操作时异或和为 \(0\) 那么对方操作时一定异或和不为 \(0\) 进而对方可以使你异或和再次为 \(0\)
3. 必输局面就是一种异或和全为 \(0\) 的情况

证毕

点击查看代码

#include <bits/stdc++.h>
using namespace std;

const int N = 5e5 + 0721;
int a[N];
int n;

int main() {
    scanf("%d", &n);
    int tmp = 0;
    for (int i = 1; i <= n; ++i) {
        scanf("%d", &a[i]);
        tmp ^= a[i];
    }

    if (tmp) {
        int loc, val;
        for (int i = 1; i <= n; ++i) {
            if ((a[i] ^ tmp) < a[i]) {
                val = a[i] - (a[i] ^ tmp);
                a[i] = a[i] ^ tmp;
                loc = i;
                break;
            }
        }
        printf("%d %d\n", val, loc);
        for (int i = 1; i <= n; ++i) printf("%d ", a[i]);
    } else
        printf("lose");

    return 0;
}

---

B.数字游戏

首先有这么个事

• 如果我操作时面对的是 \(1\) 那么我必输

显然

然后可以发现这么个事

• 如果我操作时面对的 \(2\) 那我一定可以 win

因为我 \(-1\) 之后对方就会面对 \(1\)

进而我们还可以发现这么个事

• 如果我操作时面对的是奇数那我一定可以 win

很简单 我直接除以自己

讨论面对偶数时的状况

这时我可以除掉任意个奇数质因子的积

摆烂了粘题解吧（

点击查看代码

#include <bits/stdc++.h>
using namespace std;

bool prime(int x) {
    if (x == 1) return 0;
    for (int i = 2; i * i <= x; ++i) {
        if (x % i == 0) return 0;
    }
    return 1;
}

int main() {
    int T;
    scanf("%d", &T);
    while (T--) {
        int n;
        scanf("%d", &n);
        if (n == 1) {
            printf("FastestFinger\n");
            continue;
        }
        if (n == 2) {
            printf("Ashishgup\n");
            continue;
        }
        if (n & 1) {
            printf("Ashishgup\n");
            continue;
        }
        int sum = 0;
        while (!(n & 1)) {
            ++sum;
            n >>= 1;
        }
        // cout << n << endl;
        if (prime(n)) {
            if (sum == 1) {
                printf("FastestFinger\n");
                continue;
            } else {
                printf("Ashishgup\n");
                continue;
            }
        } else if (n == 1) {
            printf("FastestFinger\n");
            continue;
        }
        else {
            printf("Ashishgup\n");
            continue;
        }
    }

    return 0;
}

---

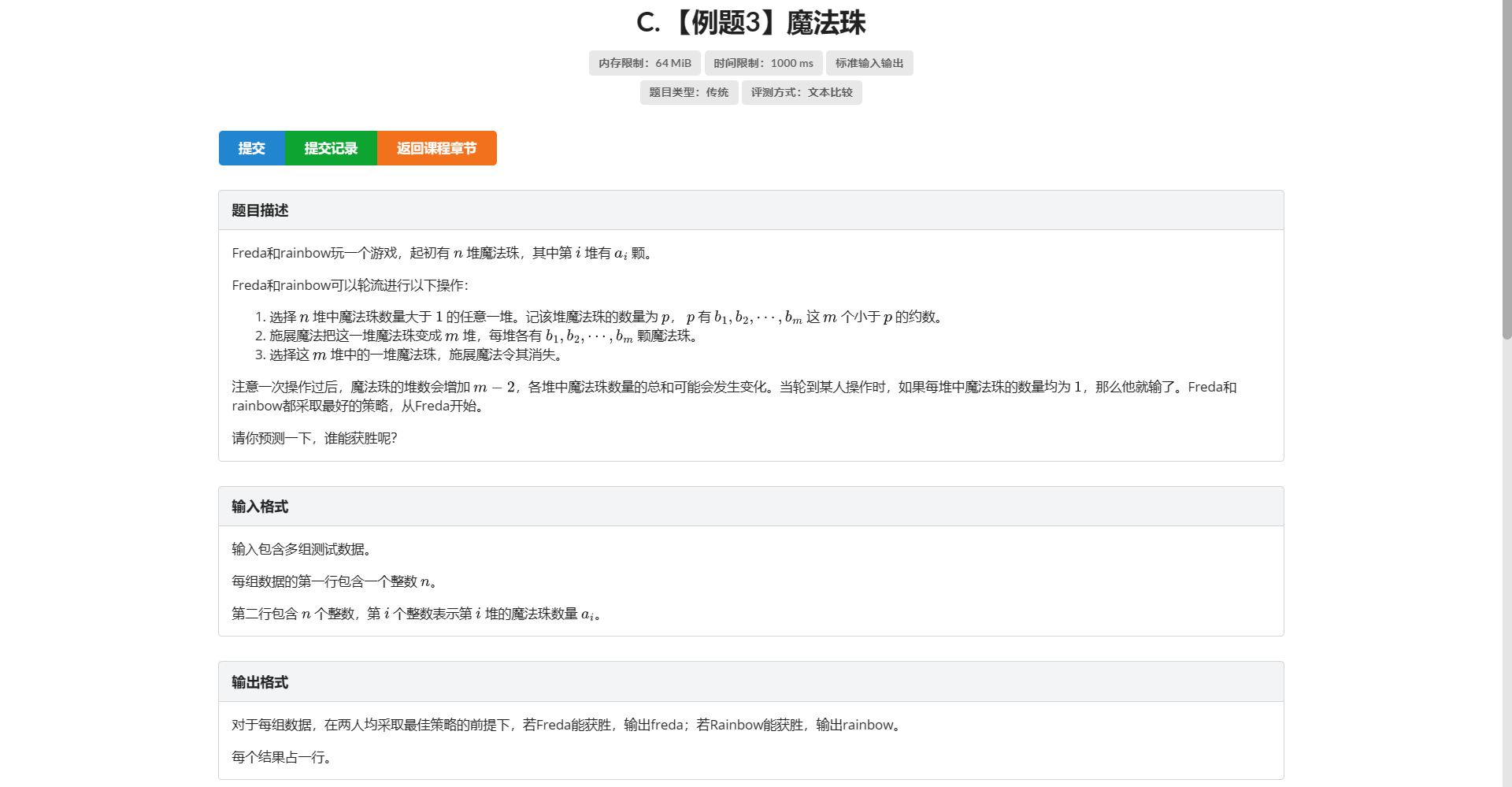
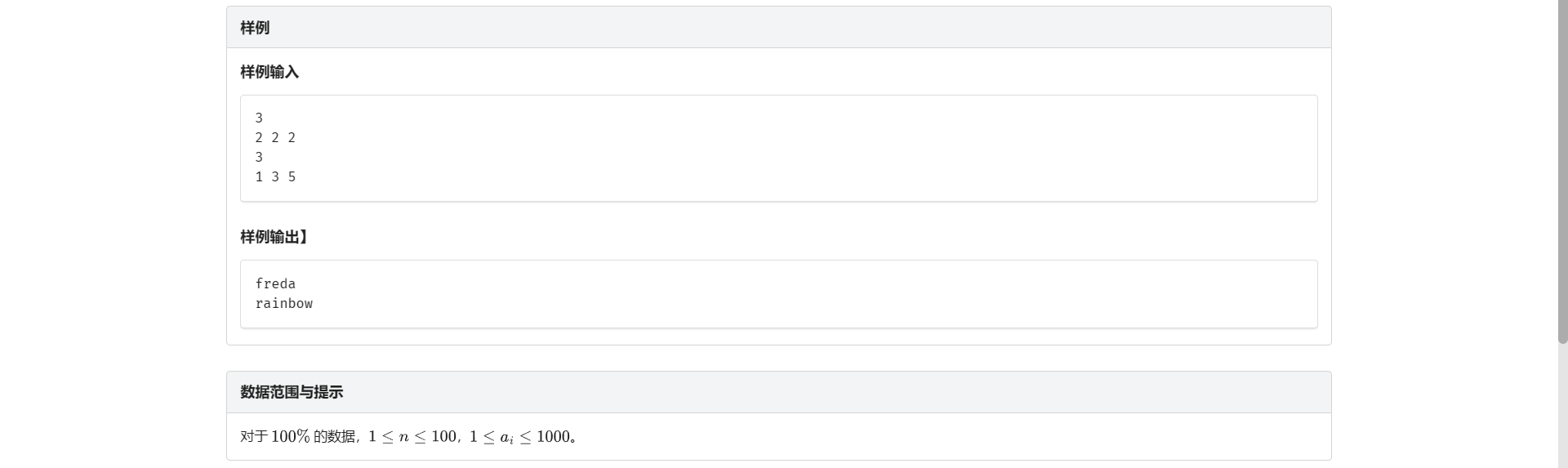
C.魔法珠

怎么感觉除了我都觉得这题的 SG 很显然。。。

SG 函数等基础知识这里就不再赘述

主要讲一下这个转移是什么意思

考虑给 DAG 建一个超级源点 其 \(h\) 值为所有入度为 0 的点的 SG 的异或和

那么考虑对于一个点能转移到的后继状态而言 比如当前这个点能变成 \(x_1, x_2, ..., x_s\) 这些堆石子
那么就可以用这些石子的异或和等于 \(h\) 来表示这个状态
那么 SG 值就是这些后继状态的 \(h\) 取 mex