2023暑假模拟

赛时记录

8:00 开题 遍历题目
T1树形DP T3 DS 怎么T2考期望？？？
感觉部分分都拿不到 决定先把T1和T3的分拿了

40min胡了个T1解法 但是手推样例发现结果不太对 是我题意理解有问题？发现选取顺序不同也会影响答案 那好像是对了
但是对于解法的正确性仍有疑问 决定等会写拍
发现忘了线性逆元咋写了 算了那就快速幂吧 反正复杂度是对的

1h10min 码过小样例 决定先看下T3再回来写拍

2h 发现T3的60pts部分分可以拆成10 + 20 + 30写

2h30min 发现30不太好写 还要记录很多东西 发现20要开vector记录位置 让原本就不富裕的空间雪上加霜 寄

2h45min 想到T2的10分部分分 结果因为要记录方案数结果long long炸了 寄

还剩十分钟 想明白T3那30怎么写了 但是没啥时间了
其实把T3那两个部分分合起来就是能过所有数据的解法 但是空间不够用

预计：100 + 0 + 10
实际：30 + 0 + 0
修锅之后：100 + 0 + 0

---

赛后总结

赛后才发现T1我写那个就是求联通块的 \(DP\) 方法啊。。
但是是挂了

upd：数据锅了 少一条边可还行 写的是正解

看着很下饭 但拿不到的分确实是拿不到 也是服气

---

T1

link

实际就是要求分成若干个联通块的方案数 考虑把一个树分成 \(i\) 个联通块 那么一定要断掉 \(i - 1\) 条边
并且断边方案和分联通块的方案一定是一一对应的
所以把一个树分成 \(i\) 个联通块的方案数 就等于从 \(n - 1\) 条边里选出 \(n - i\) 条边的方案数

然后我们要从 \(k\) 个颜色中选出 \(i\) 个颜色给这些联通块染色 并且颜色顺序是有影响的 所以是 \(A_{k}^{i}\)

答案就是 \(\sum\limits_{i = 1}^k C_{n - 1}^{i - 1} * A_{k}^{i}\)

---

T2

link

挂了的图长这样

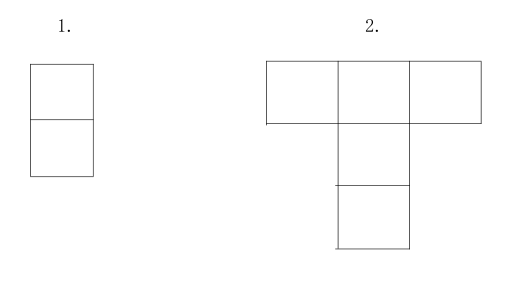
实际上期望是个幌子 我们求出方案数之和和这些方案的覆盖面积之和除一下就行

首先我们考虑没有“某些列必须至少覆盖一格”的条件怎么做

考虑状压 设 \(f_{i, S}\) 表示当前在第 \(i\) 列放置状况为 \(S\) 的方案数

然后发现我们放骨牌可能和下一列 下下一列产生影响
所以我们考虑把下两列都状压进去 所以数组意义更改：表示下两列放置情况为 \(S\) 的方案数

然后注意如果暴力枚举 每次转移就是 \(2^{16} * 2^{16}\) 就炸掉了
我们预处理出每个状态可能到达的状态 建一个自动机
然后转移即可

那么加上限制条件 我们容斥即可

---

T3

link

首先考虑 如果我们把这个问题抽象成涨潮 那么我们记录每个上坡的第一个点

然后我们把每一个区间询问都改成前缀和相减的形式

那么我们考虑说假如我们把 \(a_i\) 这个点拔高 使其超过 \(a_{i - 1}\) 和 \(a_{i + 1}\)
所以对于后面所有高度在 \(\left[a_{i - 1}, a_i\right]\) 的询问 它就会产生 \(1\) 的贡献
所以我们对于每个 \(k\) 我们要查询满足这样的修改的贡献之和：

• 这个修改在这个询问之前
• 这个修改的位置在这个询问的位置之前
• 这个修改的影响值域包含这个询问对应位置的点的大小
  这就是个三维偏序