2023.8.12 莫队

[HNOI2016] 序列

luogu link

考虑莫队 我们考虑加入一个点对于当前区间的贡献 设 \(min_{l, r}\) 表示 \(\left[l, r\right]\) 的最小值的话 \(r\) 右移对区间的贡献就是 \(\sum\limits_{j=l}^{r} min_{j, r}\) 发现这是个后缀最小值的形式

那么我们考虑每个区间最小值 显然就是一个单调不降的序列 那么实际上就可以用单调栈来维护这个东西

但是我们好像还是不太做删除操作 然后就卡死在这了

正解：我们考虑如何 \(O(1)\) 的查询贡献
设 \(f_i = \sum\limits_{i = 1}^r min_{i, r}\)
那么查询 \(a_r\) 对 \(\left[l, r\right]\) 的贡献 我们首先查到 \(\left[l, r\right]\) 的区间最小值所在的位置 我们设其为 \(p\)
贡献就是 \(f_r - f_p + a_p * (p - l + 1)\)

画个图理解下 其中黑线表示 \(f_r\) 红线表示 \(f_p\) 蓝线表示 \(f_l\)

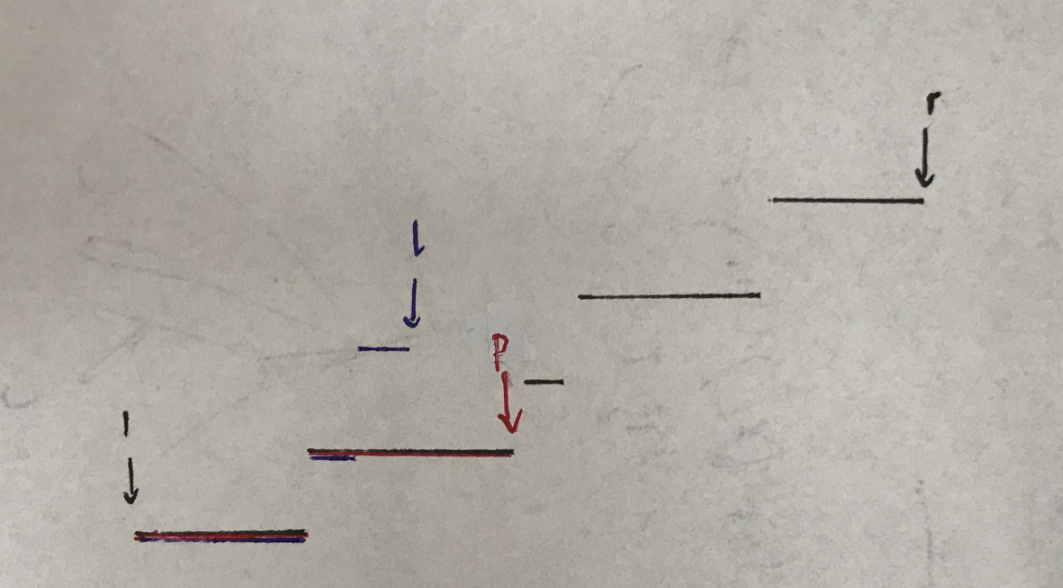
那么这个 \(p\) 就可以用 \(ST\) 表来 \(O(1)\) 查询 这样每次移动就是 \(O(1)\)

当然 我们向左移动端点就要另开一个后缀和数组 其余操作都同理

总复杂度 \(O(n \sqrt n)\)

---

[JOISC2014]歴史の研究

luogu link

回滚莫队 适用于只能添加/删除的莫队
以这道题为例 我们只能添加

那么对于左端点在同一个块内的询问 我们每次都从这个块的最右端开始左移左端点
具体地 首先假设这个块的右边界为 \(r\) 我们使 \(nowl = r + 1, nowr = r\) 对于左右端点都在块内的询问 我们直接暴力做 那么对于剩下的询问 每次先移动右端点 然后记录此时状态 然后左移左端点到该位置 统计答案 然后回到还没移动左端点时的状态