2025.07.01 CW 模拟赛 C. 列序号括

C. 列序号括

原题链接.

题目描述

小 Z 是括号序列的狂热爱好者，对特殊的括号序列更是情有独钟。

由于研究过过多的括号序列，小 Z 已经对各种各样的括号序列计数、权值转换、前后缀求和失去兴趣了，它决定来解决最小字典序问题。在下面的描述中，我们规定左括号 ( 的字典序小于右括号 )。

小 Z 首先生成了一个括号序列，希望通过若干次操作使得剩下的括号序列字典序最小。

我们定义一次操作可以删除位置 \(i\) 和 \(j\) 上的字符，当且仅当：

• \(i < j\)
• 位置 \(i\) 的字符为左括号 (
• 位置 \(j\) 的字符为右括号 )

小 Z 已经轻松解决了这个问题，现在想让你写一份程序来验证其正确性。

---

思路

首先需要观察到一个的性质:

• 如果删除 \((i, j)\) 这对括号, 那么最终序列中 \((i, j)\)​ 之间的所有括号都需要被删空, 否则一定不优/能够通过其他方式代替.

同时根据这个性质我们可以将问题转化为可以在原串中选取若干连续合法括号串并删去, 使得字典序最小.

如果我们从前往后做, 会有一个问题: 若 \(S\) 为 \(S'\) 的前缀, 那么 \(S < S'\), 但是选择 \(S\) 不一定更优.
简单来讲, 从前往后直接贪心会产生后效性.

我们如果倒序处理这件事情, 贪心就是正确的了.
具体一点, 我们从后往前遍历整个序列, 用一个栈来维护当前遍历过的字符, 并找到与当前字符「匹配」的右括号 \((\) 如果是当前字符为右括号就是它自己 \()\). 如果当前字符为左括号, 我们就需要考虑这一对括号是否会被删去. 具体操作我们采用贪心, 假设当前合法对的左, 右括号下标分别为 \(x, y\), 我们只需要将其与 \(y\) 右侧 \(y - x + 1\) 个字符相比较即可 \((\) 因为如果删去当前合法对, 右边 \(y - x + 1\) 个字符会补上来 \()\).

这样暴力比较是正确的, 复杂度最劣为 \(\mathcal{O}(n \log n)\).
考虑一段合法括号串, 比较如下图

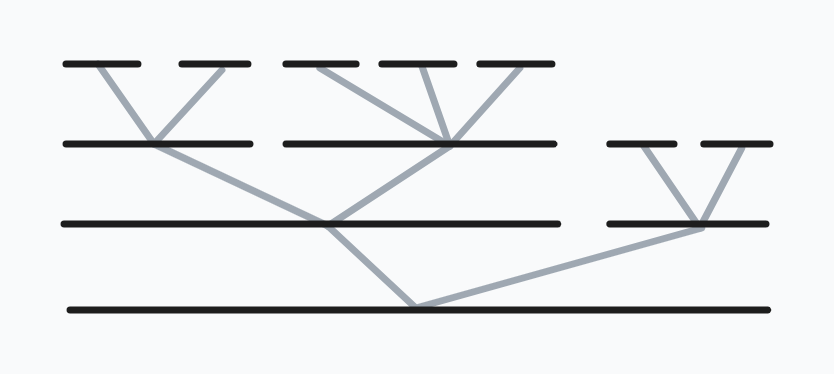
形成了一颗树的形式, 而这颗树的深度一定不会超过 \(\log n\) 层, 自然总比较次数也就不会超过 \(n \log n\) 次了.

#include <iostream>
#include <cstring>
using namespace std;

int n, top, nxt[1000001];
char s[1000001], st[1000001];

void init() {
	scanf("%s", s + 1);
	n = strlen(s + 1);
}

void calculate() {
	auto check = []() -> bool {
		int l = top, r = nxt[top];
		while (r and l > nxt[top]) {
			if (st[l] != st[r]) {
				return st[r] > st[l];
			}
			--l, --r;
		}
		return r > 0;
	};
	for (int i = n; i; --i) {
		if (s[i] == ')') {
			st[++top] = ')', nxt[top] = top;
		} else {
			st[++top] = '(';
			nxt[top] = max(-1, nxt[top - 1] - 1);
			if (~nxt[top] and !check()) {
				top = nxt[top];
			} else {
				nxt[top] = nxt[nxt[top]];
			}
		}
	}
	for (int i = top; i; --i) {
		putchar(st[i]);
	}
}

void solve() {
	init(), calculate();
}

int main() {
	solve();
	return 0;
}