2025.04.10 CW 模拟赛 C. 穿越银匙之门

C. 穿越银匙之门

原题: [AGC027F] Grafting.

题目描述

给定两棵 \(n\) 个节点的书 \(A, B\), 你需要对 \(A\) 执行若干次操作, 每次操作选择一个叶子结点, 删除链接这个叶子的边, 并将这个叶子结点连向任意一个另外的店, 每个点只能被选择一次.

求使得 \(A, B\) 相同的最小的操作次数. 有 \(T\) 组测试数据.

\(T \le 20, n \le 50\).

---

思路

首先, 如果两棵树相同, 直接输出 \(0\).

一个朴素的想法是我们每次钦定一个点为根节点, 也就是不操作它, 然后对于整棵树进行操作. 由于我们钦定了根节点, 所以操作次数上限为 \(n - 1\) 次.

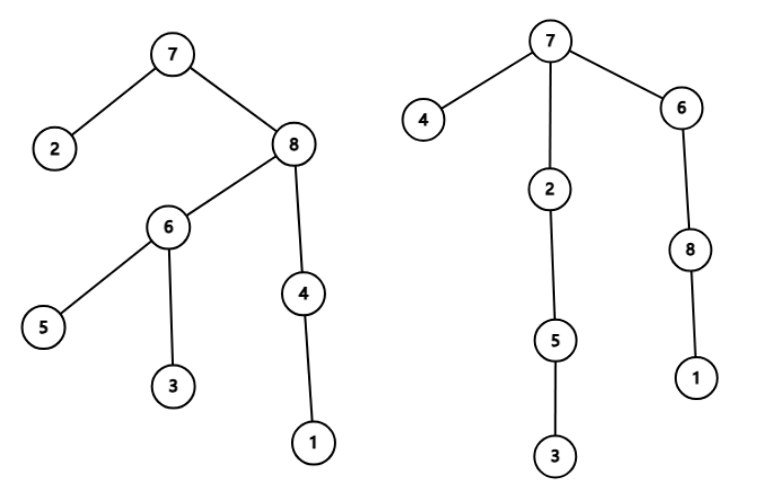
但是存在操作次数为 \(n\) 的例子! 如下图, 一种最优操作顺序为 \((2, 1), (5, 2), (3, 5), (7, 2), (6, 7), (8, 6), (4, 7), (1, 8)\) 一共 \(8\) 次操作, 其中 \((u, v)\) 表示将 \(u\) 接到 \(v\) 上.

所以我们不能钦定一个点 \(i\) 不动, 而是再枚举一维 \(j\), 表示先将 \(i\) 接到 \(j\) 上, 然后钦定 \(i\) 为根节点.

有了根节点, 考虑如何计算操作次数. 我们记 \(faA, faB\) 分别表示 \(u\) 在 \(A, B\)​ 中的父亲.

一个点需要被操作当且仅当 \(faA_u \ne faB_u\).

于是一种显然无解的情况是 \(u\) 不需要操作, 但是 \(faA_u\) 需要被操作. \((\)因为一个点只能够被操作一次, 不可能将 \(u\) 移走再移回来\()\)

同时由于每次只能操作叶子结点, 所以操作需要有一定的顺序

• 当 \(u\) 和 \(faA_u\) 均需要被操作时, 需要先操作 \(u\), 再操作 \(faA_u\).
• 当 \(u\) 和 \(faB_u\) 均需要被操作时, 需要先操作 \(faB_u\) 到正确的位置, 再操作 \(u\) 接在 \(faB_u\) 后方.

依次我们进行连边, 可以得出一个有向图. 再在图上跑拓扑排序即可, 判断是否合法的依据就是能否成功拓扑排序. 总时间复杂度 \(\mathcal{O}(Tn^3)\).

int topo() {
	int cnt = 0, tot = 0;
	for (int i = 1; i <= n; ++i) {
		vis[i] = faA[i] != faB[i];
		cnt += vis[i];
		e[i].clear(), ind[i] = 0;
	}
	for (int i = 1; i <= n; ++i) {
		if (!vis[i] and vis[faA[i]]) {
			return -1;
		}
	}
	for (int i = 1; i <= n; ++i) {
		if (!vis[i]) {
			continue;
		}
		if (vis[faA[i]]) {
			e[i].push_back(faA[i]);
			++ind[faA[i]];
		}
		if (vis[faB[i]]) {
			e[faB[i]].push_back(i);
			++ind[i];
		}
	}
	for (int i = 1; i <= n; ++i) {
		if (vis[i] and !ind[i]) {
			q.push(i);
		}
	}
	while (!q.empty()) {
		int u = q.front();
		q.pop(), ++tot;
		for (int v : e[u]) {
			if (!(--ind[v])) {
				q.push(v);
			}
		}
	}
	return tot != cnt ? -1 : tot;
}

---

后话

遇到操作具有先后顺序方面的题可以向拓扑排序上面靠.