2025.04.08 CW 模拟赛 B. 摸鱼军训

B. 摸鱼军训

题目描述

冒泡演出是 CS 大学的军训结束表演，由 \(n\) 位同学组成，每位同学都领取一个从 1 到 \(n\) 的编号，同学们的编号两两不同。

冒泡演出的内容很简单，刚开始 \(n\) 位同学站成一排，同学们的编号形成一个排列 \(a[1 \ldots n]\)，教官每吹一次哨，同学们就进行一次冒泡排序：

for (int i = 1; i < n; i++) {
    if (a[i] > a[i + 1]) swap(a[i], a[i + 1]);
}

众所周知，教官至多吹 \(n - 1\) 次哨后，同学们手中的编号恰好就会形成升序排列 \(1, 2, \ldots, n\)，不过因为同学们都想摸鱼，所以 \(n\) 位同学一共提出了 \(q\) 个以下格式的询问：

• \((k, x)\)：询问持有编号 \(x\) 的同学在教官吹 \(k\) 次哨后所在位置的下标。

思路

不妨设 \(pre_i\) 表示 \(a_i\) 前面比 \(a_i\) 大的数的数量, \(pos_x\) 表示数 \(x\) 所在的位置. 我们分以下三类情况进行讨论

1. \(k \le pre_i\). 经过模拟可以发现, 每次我们会将一个在 \(i\) 之前的一个比 \(x\) 大的数挪到 \(i\) 之后, 进而使得 \(a_i\) 向前挪动一次. 故答案为 \(pos_x - k\).

2. \(k \le n - x\)​. 对于这种情况, 排列中 \(x \sim n\)​ 的数一定全部归位了, 所以答案就是 \(x\)​.

3. 对于剩下的情况, 答案是「在 \(pos_x\) 后第 \(k - pre_i\) 个比 \(x\) 大的数的下标减去 \(k\)」.

   

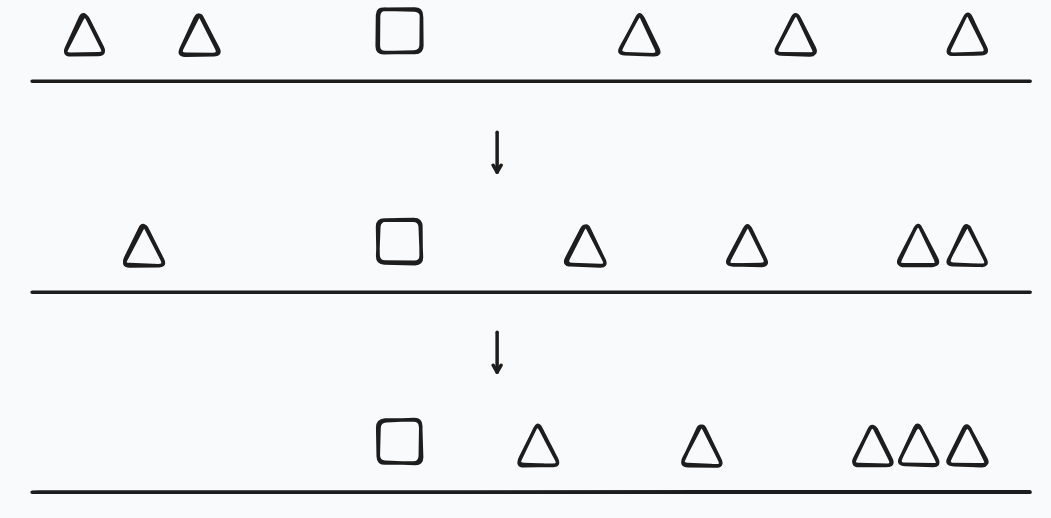
   考虑证明一下. 如上图, 正方形表示 \(x\), 三角形表示比 \(x\) 大的数. 同时, 我们定义一次「碰撞」表示两个三角形相邻的时刻.

   分类讨论「碰撞」时刻

   • 如果前面的三角形比后面的三角形大, 那么两个三角形的位置会进行交换. 后面的三角形会挪到前面一个位置. 前面的三角形继续往后移动.
   • 如果前面的三角形比后面的三角形小, 则前面的三角形会停留在后面的三角形前面的一个位置. 后面的三角形继续移动.

   以此类推, 我们发现除了最后归位的三角形, 每个三角形都会向前挪动 \(k\) 次! 在第 \(k\) 次操作后 \(x\) 会停留在 \(pos_x\) 后第 \(k - pre_i\) 个比 \(x\) 大的三角形下标减去 \(k\) 就是这么来的. 至于为什么是第 \(k - pre_i\) 个是因为前面 \(pre_i\) 次操作我们需要将 \(x\) 前面的三角形挪动到后面.

在实现上, 我们将询问离线, 按 \(x\) 降序排序, 那么原序列就会转成一个 \(0,1\) 序列, 「\(pos_x\) 后第 \(k - pre_i\) 个比 \(x\) 大的数的下标」相当于在整个序列上第 \(k\) 个为 \(1\) 的下标, 线段树上二分即可. 时间复杂度 \(\mathcal{O}((n + q) \log n)\).

#include <iostream>
#include <algorithm>

using namespace std;

char buf[1 << 20], *p1, *p2;
#define getchar() (p1 == p2 and (p2 = (p1 = buf) + fread(buf, 1, 1 << 20, stdin), p1 == p2) ? 0 : *p1++)

int read() {
	int x = 0; char c = getchar();
	while (c < '0' or c > '9') {
		c = getchar();
	}
	while (c >= '0' and c <= '9') {
		x = x * 10 + (c & 15);
		c = getchar();
	}
	return x;
}

void print(int x) {
	if (x > 9) {
		print(x / 10);
	}
	putchar(x % 10 ^ 48);
}

constexpr int N = 500001;

int n, m, pos[N], pre[N], ans[N];
int P = 1, DEP, tr[N * 3];
bool vis[N];
struct Query {
	int k, x, id;
	friend bool operator<(Query x, Query y) {
		return x.x > y.x;
	}
} q[N];

void update(int x) {
	x += P, ++tr[x];
	for (x >>= 1; x; x >>= 1) {
		tr[x] = tr[x << 1] + tr[x << 1 | 1];
	}
}

int query(int l, int r) {
	l += P - 1, r += P + 1;
	int res = 0;
	while (l ^ 1 ^ r) {
		if (~l & 1) {
			res += tr[l ^ 1];
		}
		if (r & 1) {
			res += tr[r ^ 1];
		}
		l >>= 1, r >>= 1;
	}
	return res;
}

int query_kth(int k) {
	int l = 1, dep = 0;
	while (dep < DEP) {
		if (tr[l << 1] >= k) {
			l <<= 1;
		}
		else {
			k -= tr[l << 1];
			l = l << 1 | 1;
		}
		++dep;
	}
	return l - P;
}

void init() {
	n = read();
	for (int i = 1; i <= n; ++i) {
		int x = read();
		pos[x] = i;
	}
	m = read();
	for (int i = 1; i <= m; ++i) {
		q[i] = {read(), read(), i};
	}
	sort(q + 1, q + m + 1);
	while (P <= n + 1) {
		++DEP;
		P <<= 1;
	}
}

void calculate() {
	for (int i = n, ptr = 1; i; --i) {
		int pre = query(1, pos[i]);
		while (q[ptr].x == i and ptr <= m) {
			int k = q[ptr].k, id = q[ptr].id;
			if (k <= pre) {
				ans[id] = pos[i] - k;
			}
			else if (k <= n - i) {
				ans[id] = query_kth(k) - k;
			}
			else {
				ans[id] = i;
			}
			++ptr;
		}
		update(pos[i]);
	}
	for (int i = 1; i <= m; ++i) {
		print(ans[i]);
		putchar('\n');
	}
}

void solve() {
	init();
	calculate();
}

int main() {
	solve();
	return 0;
}