对有向图最小平均权值回路的讨论

对有向图最小平均权值回路的讨论

接触于模拟赛题目.

以HNOI2009 最小圈为例, 下面介绍两种求「有向图最小平均权值回路」的方法.

二分 + SPFA

显然对于最终的答案具有单调性, 我们可以进行二分.

设 \(k\) 为环上点的个数, 写出答案的形式

\[ans \le \frac{1}{k} \sum c_i \]

移项得到

\[\sum c_i - k \cdot ans \ge 0 \\ \sum (c_i - ans) \ge 0 \]

假设当前二分到的答案为 \(\rm{mid}\). 对于 \(\rm{check}\) 函数, 我们将每条边的边权减去 \(\rm{mid}\) 再跑 SPFA 判断是否有负环即可. 如果有, 说明 \(\rm{mid}\)​ 偏大, 否则偏小.

时间复杂度 \(\mathcal{O}(nm \log V)\). 但这不是讨论的重点, 接下来会介绍一种时间复杂度 \(\mathcal{O}(nm)\) 的算法.

---

Karp 算法

Karp 在 1977 年的论文中提出了一种在 \(\mathcal{O}(nm)\) 时间复杂度内解决「有向图最小平均权值回路」的方法, 具体如下:

我们令 \(s\) 表示出发点, \(F_k(u)\) 表示从 \(s\) 出发, 经过 \(k\) 条边到达 \(u\) 的最小路径权值.

定理 1. 对于最终答案, 我们可以表示为以下式子

\[ans = \min_{u \in V}\{\max_{k = 0}^{n - 1} \frac{F_n(u) - F_k(u)}{n - k}\} \]

对于定理 1 的证明我们需要一个引理.

引理 1. 如果最终答案为 \(0\), 那么

\[\min_{u \in V}\{\max_{k = 0}^{n - 1} \frac{F_n(u) - F_k(u)}{n - k}\} = 0 \]

• 证明

  因为最终答案为 \(0\), 所以原图中一定存在一个权值为 \(0\) 的环, 同时不存在负环. 所以从 \(s\) 到 \(v\) 的最短路一定存在, 并且边数不超过 \(n\), 我们令其为 \(\pi(v)\). 根据定义, 我们有 \(\pi(v) \le F_i(v)\).

  同时我们有

  \[\max_{k = 0}^{n - 1} F_n(v) - F_k(v) = F_n(v) - \pi(v) \ge 0 \]

  上式成立当且仅当 \(F_n(v) = \pi(v)\), 于是我们只需要证明存在一个节点使得 \(F_n(v) = \pi(v)\).

  令 \(C\) 表示图中一个权值为 \(0\) 的环. 不妨从 \(C\) 上任取一点 \(x\), 选定一条 \(s \to x\) 的最短路径, 亦即 \(\pi(x)\). 同时为了构造出长度为 \(n\) 的路径, 我们让 \(x\) 继续在 \(C\) 上走, 直到路径长度为 \(n\), 令其为 \(v\) 点.

  

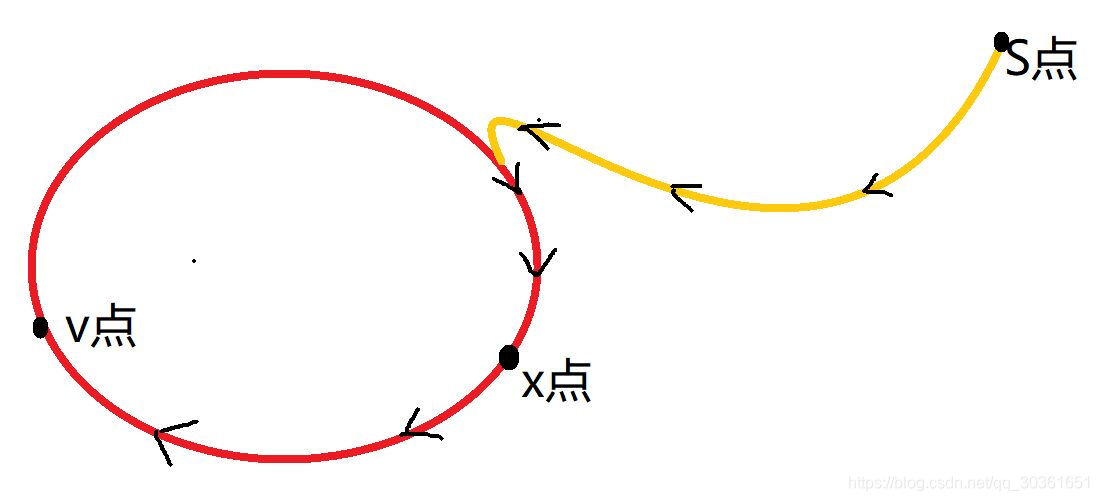
  那么我们需要证明的就是: 对于路径 \(s \to x \to v\) 一定是 \(s \to v\)​​ 的最短路径.

  我们钦定 \(dis_{u \to \dots \to v}\) 表示从 \(u\) 出发, 经过若干点到达 \(v\)​ 的路径长度.

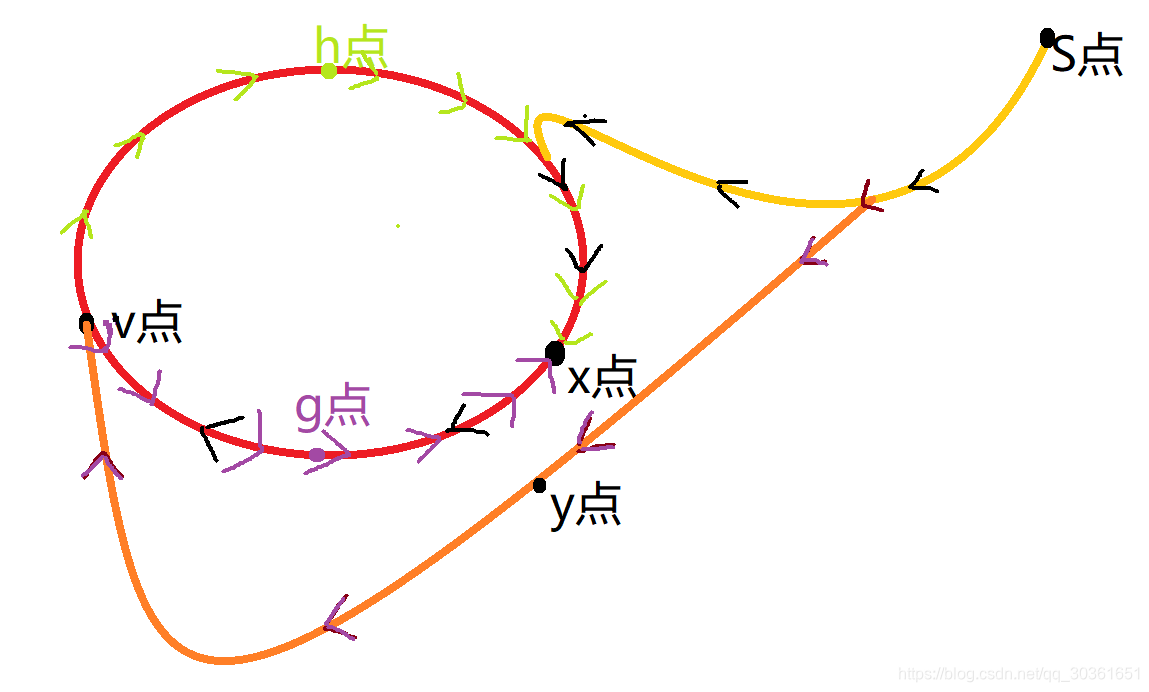
  反证法. 如下图, 假设 \(\pi(v) = dis_{s \to y \to v}\) 而不是 \(dis_{s \to x \to v}\).

  由于路径 \(dis_{x \to h \to v}\) 和 \(dis_{x \to g \to v}\) 等价, 不妨设 \(dis_{x \to g \to v} \le dis_{x \to h \to v}\). 同时因为 \(C\) 权值为 \(0\), 所以 \(dis_{x \to g \to v} + dis_{x \to h \to v} = 0\).

  所以有以下式子

  \[\pi(v) = dis_{s \to y \to v} \le dis_{s \to x} + dis_{x \to g \to v} \\ dis_{s \to y \to v} - dis_{x \to g \to v} = dis_{s \to y \to v} + dis_{v \to h \to x} \le dis_{s \to x} = \pi(x) \]

  于是惊人的发现我们找到了一条比 \(\pi(x)\) 更短的路径! 与原命题矛盾, \(\square\).

  

有了这个引理, 我们讨论当图中所有边权增加 \(c\) 后会产生什么影响. 容易发现最终答案会增加 \(c\), 所有环的平均权值增加了 \(c\). 这相当于引理式子中两侧增加了相同的量, 依旧成立, 定理就证完了.

实现. 如果图不是强联通的, 我们需要建立一个超级源点 \(0\), 向每一个点都连一条权值为 \(0\) 的边.

初始条件有

\[F_0(s) = 0, F_0(u) = + \infty, u \ne s \]

转移有

\[F_k(v) = \min_{(u, v) \in E}(F_{k - 1}(u) + w(u, v)) \]

其中 \(k\) 从 \(1 \sim n\) 进行枚举. 时间复杂度 \(\mathcal{O}(nm)\).