2025.3.10 做题记录

以个人开题顺序记录.

A. Shuffling Songs

36 分钟.

---

看到 \(n \le 16\)​ 我们可以状压.

找到最小移除次数等价于保留尽可能多的歌曲, 形式化的, 我们设一个可行性 DP: \(f_{\mathbb{S}, i}\) 表示当前选的集合为 \(\mathbb{S}\) 且最后一个选择的为歌曲 \(i\) 时是否合法.

考虑如何转移到 \(f_{\mathbb{S}, i}\). 我们可以枚举 \(\mathbb{S}\) 中的每一个 1, 将 1 的位置记为 \(j\). 如果将歌曲 \(i\) 接在歌曲 \(j\) 后面是合法的, 那么将 \(f_{\mathbb{S}, i}\) 或上 \(f_{\mathbb{S} \oplus 2^j, j}\) 即可. 时间复杂度 \(\mathcal{O}(n^2 2^n)\).

C. Vlad and Trouble at MIT

1 小时.

---

树形 DP.

根据题意, 如果在树上不包含 C 是好做的, 我们需要考虑将每一个 C 变为 P 或 S 的最小代价.

令 \(f_{u, 0 / 1}\) 表示当前节点为 P 或 S 时的最小代价. 如果 \(s_u \ne s_v\) 那么我们就需要加一堵墙. 在 DFS 回溯时更新即可.

D. Feed Cats

40 分钟.

---

被题面硬控 5 分钟.

不管怎样, 我们首先可以令 \(f_i\) 表示到第 \(i\) 步时的最大贡献, 显然第 \(i\) 步有喂或者不喂两种策略.

题目中要求不能有任何两只猫被喂了超过 1 次, 我们需要考虑在什么条件下转移的两个集合不交.

令 \(mxr_i\) 为第 \(i\) 步时所有 \(l_j \le i \le r_j\) 中最大的 \(r_j\). 显然, 当 \(i > mxr_j\) 时两区间一定不交, 同时也可以看出我们是从一段 \(f_i\) 的前缀转移而来, 记录一下前缀最大值, 每一步选的贡献差分前缀和计算即可. 时间复杂度 \(\mathcal{O}(n)\).

F. Sasha and a Walk in the City

1 小时.

---

最开始想错了, 以为集合内最多只会有两个数. 结果发现下图也是合法的. \((\)红点表示「危险」点\()\)

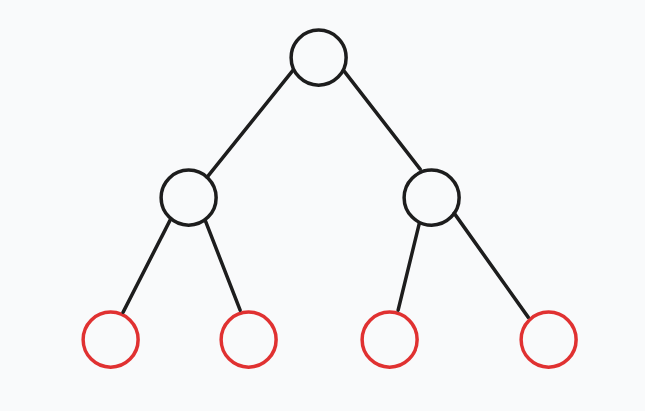
由于是统计方案数, 我们可以考虑 DP.

• \(f_{u, 0 / 1 / 2}\) 表示以 \(u\) 为根的子树内, 任意节点到根节点路径上最多会经过 0, 1, 2 个「危险」点的方案数.

考虑怎么转移, 给出式子:

\[\begin{cases} f_{u, 0} = 1 \\ f_{u, 1} = \prod_{v \in son(u)} f_{v, 0} + f_{v, 1} \\ f_{u, 2} = \sum_{v \in son(u)} f_{v, 1} + f_{v, 2} \end{cases} \]

解释一下, \(f_{u, 1}\) 的转移是因为在所有子树我们都可以任选, \(+ f_{v, 0}\) 是因为我们可以钦定 \(u\) 为「危险」点. \(f_{u, 2}\) 由于到根节点的黑点数量最多为 2, 我们不能任选了, 所以方案数是加起来的.

感觉没什么太重要的性质, 凭感觉猜出来的.

B. Messenger in MAC

看的题解. 上午没有想到怎么最小化 \(b_i\) 的贡献, 糖丸了.

其实可以直接对 \(b_i\) 升序排序, 贡献直接就是最小的了, 为 \(b_{p_k} - b_{p1}\).

剩下就是正常 DP 了, \(f_{i, j}\) 表示当前枚举到第 \(i\) 个, 选了 \(j\) 个的方案数减去 \(b_i\). 由于 \(n \le 2000\), 转移需维护前缀最大值.

答案即为 \(f_{i, j} + b_i \le l\) 的最大的 \(j\).