左偏树

左偏树

概念

左偏树是一种常用可并堆, 可以在 \(\mathcal{O}(\log n)\) 的时间内合并两个堆.

可并堆顾名思义, 是指除了堆的普通操作, 还支持合并的堆. 有如配对堆, 二项堆, 斐波那契堆等等.

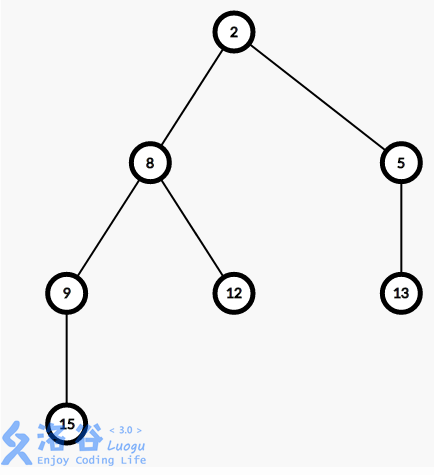
相关定义

• 外节点: 子节点数小于两个的节点, 即左右儿子至少有一个为空的节点.
• 距离 \(\rm{dist}\): 一个节点到它子树中离它最近的外节点的距离, 即两点间边的数量. 空节点的 \(\rm{dist} = 0\).
• 左偏树: 一种满足「左偏」性质的堆有序二叉树 (「左偏」性质体现在左儿子的 \(\rm{dist}\) 均大于 右儿子的 \(\rm{dist}\)).
• 左偏树的距离: 我们将一棵左偏树根节点的距离作为该树的距离.

性质

• 满足堆的基本性质.
• 对于任意节点, 左儿子的距离均大于右儿子的距离, 且该节点的距离等于其右儿子的距离加一.
• 对于一颗 \(n\) 个节点的左偏树, 其根节点的距离不超过 \(\log n\)​.

---

基本操作

以下的「堆」均默认为「小根堆」.

合并

合并是左偏树最核心的操作.

在合并两个堆时, 由于要满足堆的性质, 先取值较小的那个根作为合并后堆的根节点, 然后将这个根的左儿子作为合并后堆的左儿子, 递归地合并其右儿子与另一个堆, 来作为合并后的堆的右儿子. 为了满足左偏的性质, 若合并后左儿子的 \(\rm{dist}\) 大于右儿子的 \(\rm{dist}\), 就交换两个儿子.

插入节点

将节点视作一个堆, 进行合并操作即可.

删除根

合并根的左右儿子即可.

删除任意节点

这里的任意节点指的是任意编号的节点而并非任意权值的节点.

与删除根节点类似, 先将左右儿子合并, 再将合并后新的左偏树接到被删除节点的父节点上即可. 与删除根节点不同, 该操作可能导致左偏性质被破坏, 因此要从该节点一直向上检查左偏性质, 直到左偏性质没有被破坏或者到达了根节点.

代码

#include "iostream"

using namespace std;

void read() {}
template <class T, class ...T1>
void read(T &x, T1 &...y) {
	x = 0;
	char ch = getchar(); bool f = 1;
	for (; ch < '0' or ch > '9'; ch = getchar()) if (ch == '-') f = 0;
	for (; ch >= '0' and ch <= '9'; x = x * 10 + (ch & 15), ch = getchar());
	x = (f ? x : -x);
	read(y...);
}

constexpr int N = 1e5 + 10;

int n, m;
int dis[N], ls[N], rs[N], rt[N];
bool exist[N];
struct Node {
	int id, v;
	friend bool operator<(Node x, Node y) { return (x.v ^ y.v) ? x.v < y.v : x.id < y.id; }
} v[N];

void init() {
	read(n, m);
	dis[0] = -1;
	for (int i = 1; i <= n; ++i) read(v[i].v), rt[i] = v[i].id = i;
}

int find(int x) { return rt[x] == x ? x : rt[x] = find(rt[x]); }

int merge(int x, int y) {
	if (!x or !y) return x + y;
	if (v[y] < v[x]) swap(x, y);
	rs[x] = merge(rs[x], y);
	if (dis[ls[x]] < dis[rs[x]]) swap(ls[x], rs[x]);
	dis[x] = dis[rs[x]] + 1;
	return x;
}

void calculate() {
	while (m--) {
		int op, x, y;
		read(op, x);
		if (op & 1) {
			read(y);
			if (exist[x] or exist[y]) continue;
			x = find(x), y = find(y);
			if (x ^ y) rt[x] = rt[y] = merge(x, y);
		}
		else {
			if (exist[x]) {
				puts("-1");
				continue;
			}
			printf("%d\n", v[x = find(x)].v);
			exist[x] = 1;
			rt[ls[x]] = rt[rs[x]] = rt[x] = merge(ls[x], rs[x]);
			ls[x] = rs[x] = dis[x] = 0;
		}
	}
}

void solve() {
	init();
	calculate();
}

int main() {
	solve();
	return 0;
}