斜率优化

斜率优化

例题引入 & 概念

[HNOI2008] 玩具装箱

朴素 DP

令 \(f_i\) 表示枚举到第 \(i\) 个物品, 分成若干段的最小代价.

设 \(\textrm{sum}\) 数组为前缀和数组, 那么就有如下转移方程:

\[f_i = \min_{j < i} \left\{ f_j + (i - (j + 1) + sum_i - sum_j - L)^2 \right\} \\ = \min_{j < i} \left\{ f_j + (i - j + sum_i - sum_j - 1 - L)^2 \right\} \]

时间复杂度 \(\mathcal{O}(n^2)\), 无法通过.

优化

为了简便, 我们钦定 \(L = L + 1, pre_i = sum_i + i\), 撤去 \(\min\), 那么转移式子就变成了 $f_i = (pre_i - pre_j - L)^2 $.

将平方拆开, 移项, 将含有相同项的合并起来:

\[f_i - (pre_i - L)^2 = f_j + pre_j^2 + 2 pre_j (L - pre_i) \]

考虑一次函数的截距式 \(y = kx + b \Rightarrow b = y - kx\), 将与 \(j\) 有关的信息转化成 \(y\) 的形式, 同时含有 \(i, j\) 的式子转化成 \(kx\), 将需要最小化的 (也就是 \(i\) 有关的) 表示为 \(b\). 具体来说, 我们令:

\[\begin{align*} & x_j = pre_j \\ & y_j = f_j + pre_j^2 \\ & k_i = 2(L - pre_i) \\ & b_i = f_i - (pre_i - L)^2 \end{align*} \]

那么转移方程就转化为: \(y_j = k_i x_j -b_i\), 将 \((x_j, y_j)\) 看作二维平面上的点, 那么 \(k_i\) 表示斜率, \(b_j\) 表示截距.

现在的问题就转化成: 选择合适的 \(j\), 使得 \(b_i\) 最小.

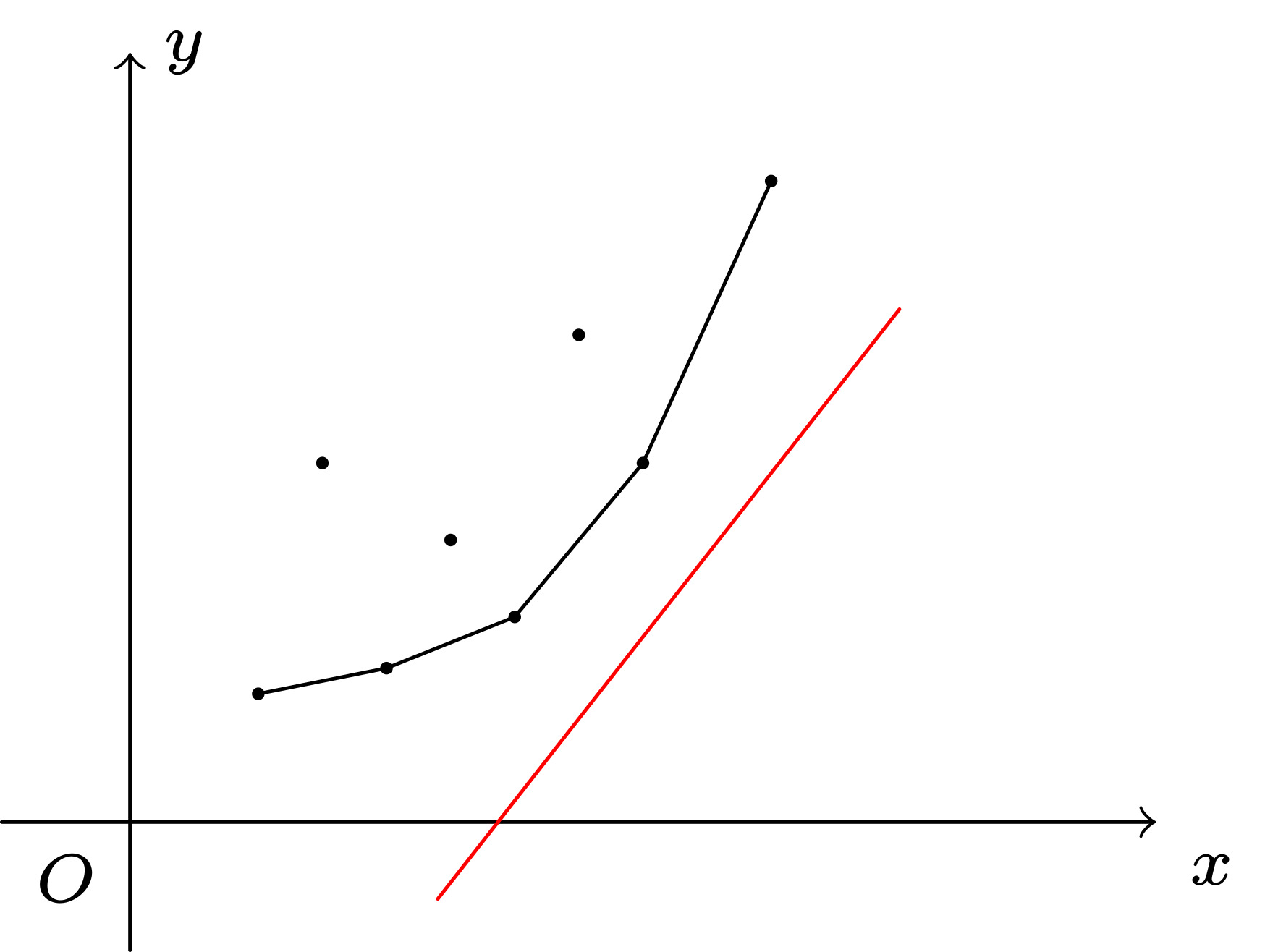
根据下凸壳的性质, 如果线段 ab 的斜率 \(< k\), 线段 bc 的斜率 \(> k\), 那么点 b 就是使得截距最小的最优点.

这样, 当 \(k, x\) 均满足单调性时, 我们可以使用单调队列来维护这个凸壳.

具体来说, 在队列中我们维护一个下凸壳, 即每两个连续点所连成的直线, 其斜率是单调上升的. 当新的点进入队列时, 确保它能够与队列中的点形成凸壳.

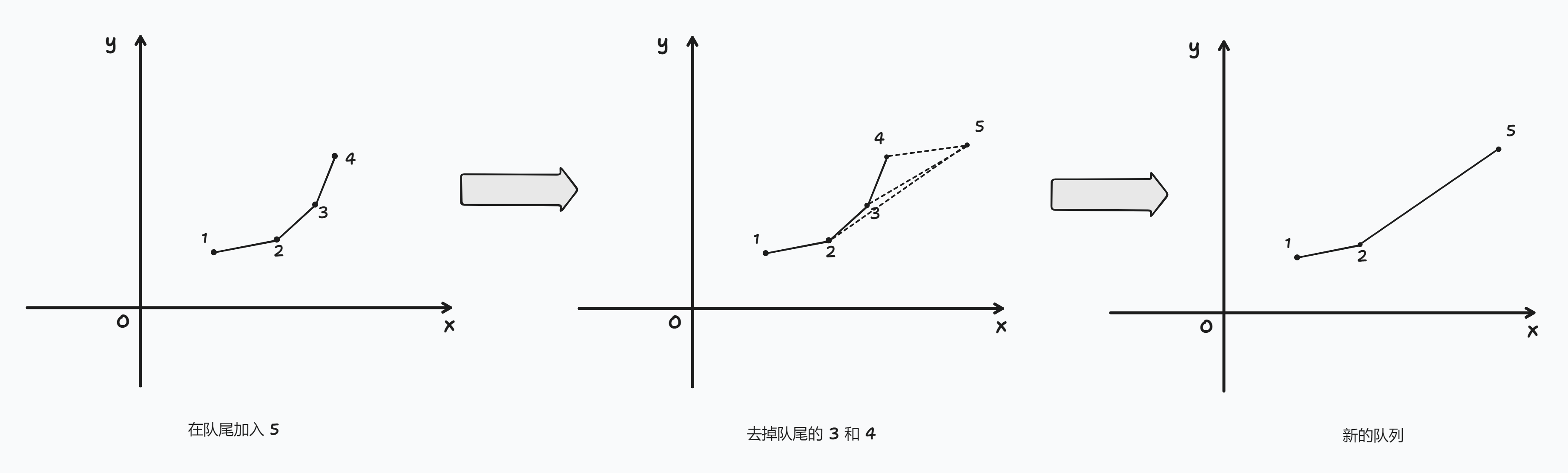
1. 如图, 队列尾部的点是 3 和 4, 准备进入队列的新点是 5. 比较点 3, 4, 5, 看线段 34 和线段 45 的斜率是否递增. 若递增, 那么 5 入队即可. 否则从队尾弹出 4, 继续比较队尾两个元素直到 5 能够入队为止.
2. 出队列, 找到最优点. 设队头的两个点为 \(p_1, p_2\), 如果 \(k_{p_1 p_2} < k\), 说明 \(p_1\) 不是最优点, 弹出. 循环往复, 直到斜率 \(> k\) 为止, 此时队头元素就是最优点 \(p^{\prime}\).

根据上述操作, 我们求解单个 \(f_i\) 是 \(\mathcal{O}(n)\) 的, 但是求解所有 \(f_i\) 还是 \(\mathcal{O}(n^2)\) 的.

事实上, \(k_i\) 是具备单调性的, 所以我们只需要用一个单调队列处理即可. 因为每一个点最多只会出队进队一次, 时间复杂度 \(\mathcal{O}(n)\).