P1715 [USACO16DEC] Lots of Triangles P

算法

计算几何, 容斥原理.

思路

首先考虑一个很简单的暴力, 我们枚举每个三角形的三个顶点, 然后枚举每一个点并且判断其是否在三角形内, 时间复杂度 \(\mathcal{O}(n^4)\).

然后就没有思路了, 看了下题解, 发现可以使用容斥进行优化.

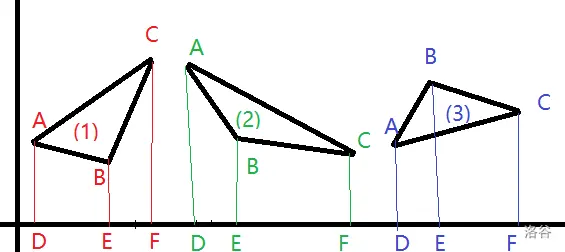
如上图, 将每个点投影到 x 轴上, 那么根据容斥, \(\rm{S}_{\triangle ABC} = S_{ADFC} - S_{ABED} - S_{BCFE}\).
那么对于图形内的树的数量, 也可以如法炮制, 只需要预处理出每两个点形成的线段下方树的数量即可.
注意对于图 1, 2, \(B\) 点可能会被算进答案, 只需要判断下并删去即可.

#include "iostream"
#include "cmath"
#include "algorithm"

using namespace std;

constexpr int N = 3e2 + 10;

int n;
struct Point {
	int x, y;
	friend bool operator<(Point x, Point y) {
		if (x.x ^ y.x)
			return x.x < y.x;
		return x.y < y.y;
	}
} p[N];

void init() {
	scanf("%d", &n);
	for (int i = 1; i <= n; ++i)
		scanf("%d %d", &p[i].x, &p[i].y);
	sort(p + 1, p + n + 1);
}

int cnt[N][N], ans[N]; // 两点下方点的数量.

bool check(int i, int j, int k) {
	double xi = p[i].x, yi = p[i].y, xj = p[j].x, yj = p[j].y, xk = p[k].x, yk = p[k].y;
	if (xk < xi or xk > xj)
		return 0;
	double K = (yi - yj) / (xi - xj);
	return yk < K * (xk - xi) + yi;
}

void calculate() {
	for (int i = 1; i ^ n; ++i)
		for (int j = i + 1; j <= n; ++j)
			for (int k = i + 1; k ^ j; ++k)
				cnt[i][j] += check(i, j, k);
	for (int i = 1; i ^ n - 1; ++i)
		for (int j = i + 1; j ^ n; ++j)
			for (int k = j + 1; k <= n; ++k)
				++ans[abs(cnt[i][j] + cnt[j][k] - cnt[i][k] + check(i, k, j))];
	for (int i = 0; i ^ n - 2; ++i)
		printf("%d\n", ans[i]);
}

void solve() {
	init();
	calculate();
}

int main() {
	solve();
	return 0;
}