笛卡尔树

前置知识: 二叉搜索树, 堆

概念

笛卡尔树是一种二叉树, 每一个节点有 \((w, k)\) 两个属性 (在算法竞赛中, \(k\) 通常为数组下标, \(w\) 为权值), 其中 \(w\) 满足堆的性质, \(k\) 满足二叉搜索树的性质.

如果笛卡尔树的 \((k,w)\) 键值确定, 且 \(k\) 互不相同, \(w\) 也互不相同, 那么这棵笛卡尔树的结构是唯一的.

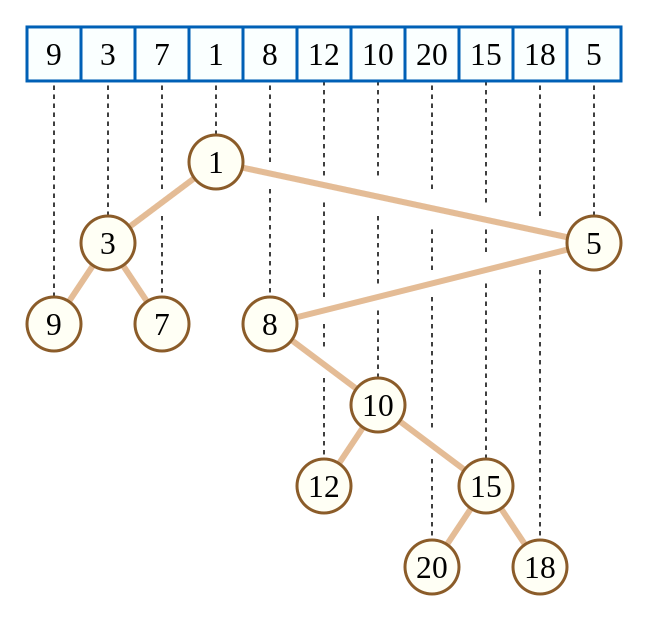
如图是一个小根笛卡尔树.

构建

我们通常利用单调栈来维护右链从而构建起笛卡尔树.

具体地, 考虑将元素按下标顺序依次插入到当前的笛卡尔树中. 那么每次我们插入的元素必然在这棵树的右链的末端. 于是我们可以从下而上地比较当前插入节点的权值与右链节点的权值, 如果找到了一个右链上的节点 \(x\) 满足 \(w_x < w_u\), 那就把 \(u\) 接到 \(x\) 的右儿子上, 而 \(x\) 原本的右子树变成 \(u\) 的左子树.

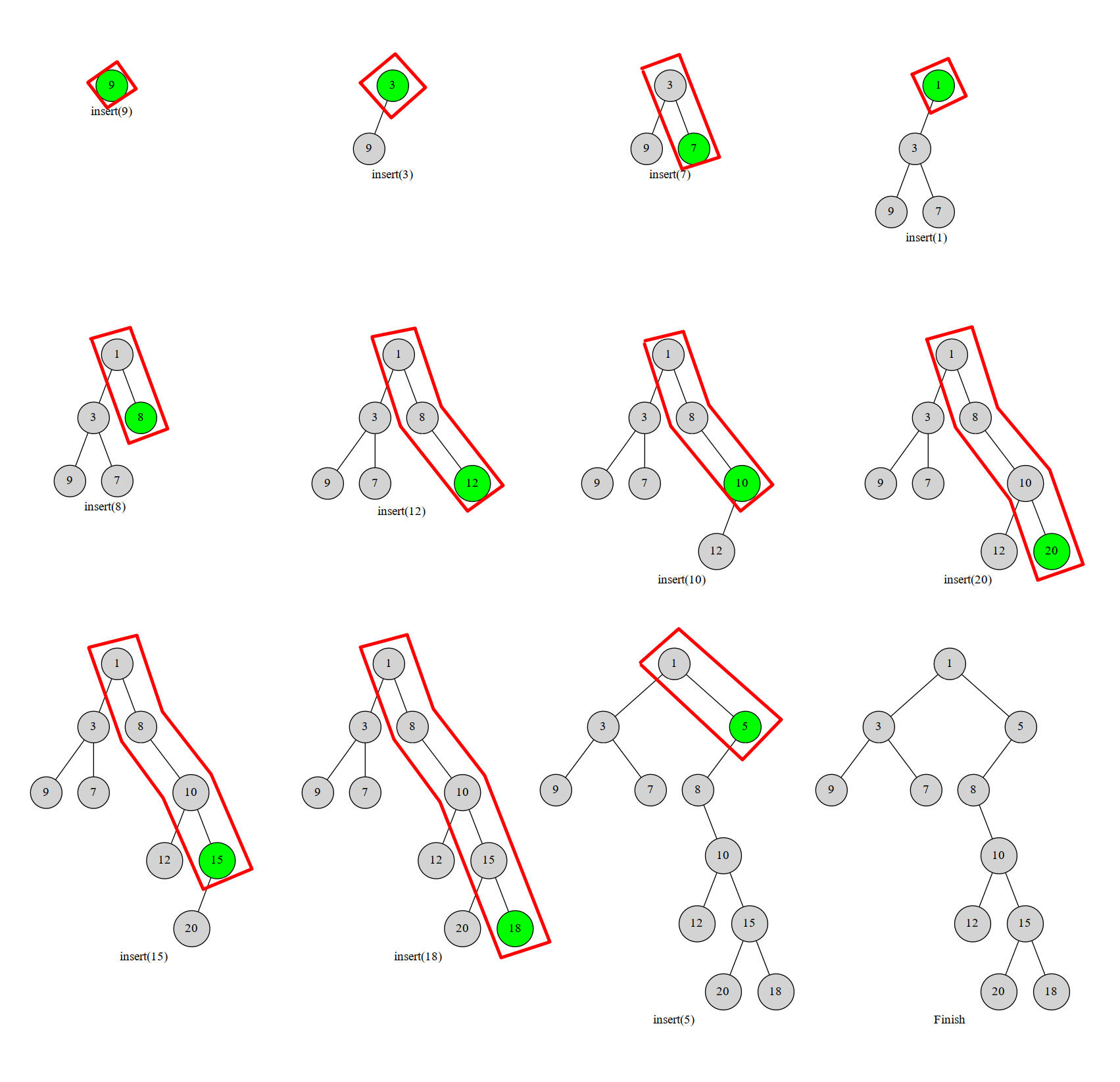
代码参考

st[++top] = 1;
for (int i = 2; i <= n; ++i) {
    while (top and p[st[top]] > p[i]) {
        --top;
    }
    if (!top) {
        ls[i] = st[top + 1];
    }
    else {
        ls[i] = rs[st[top]], rs[st[top]] = i;
    }
    st[++top] = i;
}