P8867 [NOIP2022] 建造军营

题目链接

算法

Tarjan 缩点, 树形 dp.

题意

给定一个无向连通图, 我们要选择某些点并且选择某些边 (被选择的边不能被删除), 使得当任意一条没有被选择的边被删除后我们选择的点两两连通.

求总共的方案数.

思路

容易发现一条删除后对连通性有影响的边只可能是割边,
我们对一条不是割边的边可看守可不看守,
于是可以考虑将每一个连通分量缩成一个点.

缩完点后, 图将变成一棵树. (因为缩点后形成的图连通且没有环)

我们令 \(E_i\) 表示在 \(i\) 这个连通分量里的边数;
\(P_i\) 表示连通分量 \(i\) 里的点数.

那么这个问题可以转化为:

给定一颗无根树, 每个节点都有 \(2^{E_i}\) 种方案不建造军营和 \((2^{P_i+E_i}-2^{E_i})\) 种方案建造军营.
求总共有多少种方案?

因为要统计所有的方案数, 所以我们可以考虑动态规划.

假定 1 号节点为根.
设 \(f_{u,0/1}\) 表示以 \(u\) 为根的子树中没有/有建造军营的方案总数.
但是对于 \(f_{i,1}\), 我们没法具体知道需要守护子树里的哪一条边, 不好转移.

考虑对状态增加限制.
令 \(f_{u,1}\) 表示以 \(u\) 为根的子树里建造了军营并且所有的军营一定通过已经派兵看守的边与 \(u\) 连通.
对于每个节点 \(u\), 我们强制除 \(u\) 子树外的所有点都不建军营, 同时不选 \(fa_u \rightarrow u\) 的边 (原因具体可以看下图).

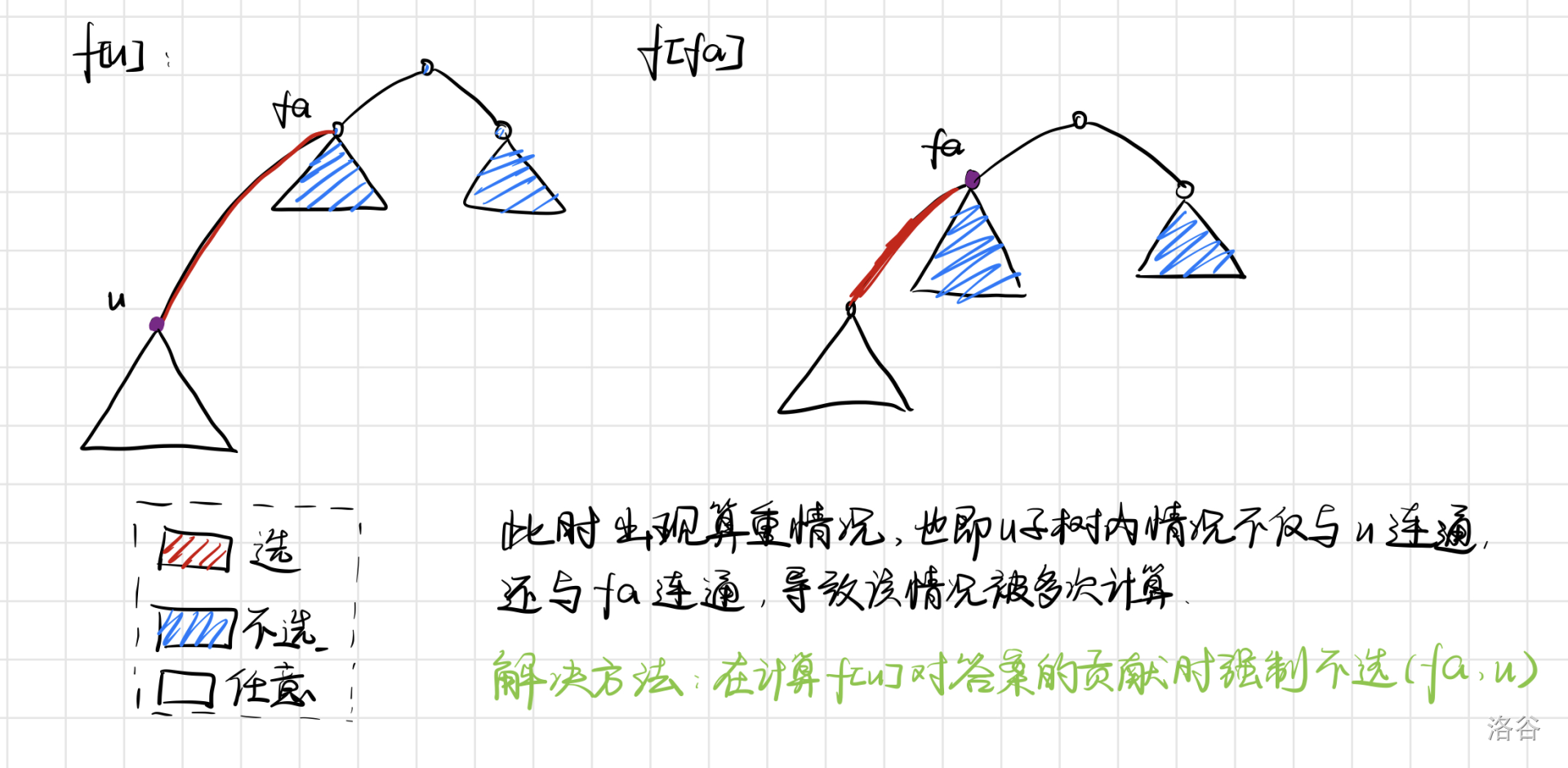
令 \(s_u\) 为以 \(u\) 为根的子树内的总边数, 那么 \(s_u = E_u + \sum_{v \in son_u} (s_v+1)\),

则有 \(ans+=f_{u,1}×2^{s_1-s_u-1}\).

而对于 1 号节点, 因为其没有父亲节点, 所以 \(ans+=f_{1,1}\).

接下来考虑转移.

对于 \(f_{u,0}\), \(f_{u,0}=2^{E_u} × \prod_{v \in son_u}2\ f_{v,0}\).
再看 \(f_{u,1}\).

• 1. 如果新增前都还未建造军营, 那么以 \(v\) 为根的子树内一定有军营, 即 \(f_{u,1}×=f_{v,0}×f_{v,1}\).
• 2. 如果新增前已经建造过军营, 那么以 \(v\) 为根的子树中军营可有可无, 且当以 \(v\) 为根的子树中没有军营时, \(v\) 与 \(u\) 是否连通均可, 故 \(f_{u,1}×=(2\ f_{v,0}+f_{v,1})\).

初始化时, \(f_{u,0}=2^{E_u},\ f_{u,1}=2^{P_u+E_u}-2^{E_u}\).

#include "iostream"
#include "stack"

using namespace std;

const int N = 5e5 + 10, mod = 1e9 + 7;

int n, m;
basic_string<int> g[N];

inline void init()
{
    cin >> n >> m;
    for (int i = 1; i <= m; ++i)
    {
        int u, v;
        cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    return;
}

class Solution
{

private:
    #define int long long

    int lw[N], dfn[N], cnt = 0;
    int sz[N], c[N], sccnt = 0;
    bool vis[N];
    stack<int> st;

    inline int qpow(int x, int y)
    {
        int ans = 1;
        while (y)
        {
            if (y & 1)
                ans = (1ll * ans * x) % mod;
            y >>= 1;
            x = (1ll * x * x) % mod;
        }
        return ans;
    }

    void Tarjan(int u, int fa)
    {
        lw[u] = dfn[u] = ++cnt;
        st.push(u), vis[u] = 1;
        for (int v : g[u])
        {
            if (v == fa)
                continue;
            if (!dfn[v])
                Tarjan(v, u), lw[u] = min(lw[u], lw[v]);
            else if (vis[v])
                lw[u] = min(lw[u], dfn[v]);
        }
        if (!(dfn[u] ^ lw[u]))
        {
            int t = -1;
            sccnt++;
            while (t ^ u)
            {
                t = st.top(), st.pop();
                sz[sccnt]++, c[t] = sccnt, vis[t] = 0;
            }
        }
        return;
    }

    basic_string<int> e[N];
    int s[N], ecnt[N];

    void dfs(int u, int fa)
    {
        s[u] = ecnt[u];
        for (int v : e[u])
        {
            if (v == fa)
                continue;
            dfs(v, u);
            s[u] += s[v] + 1;
        }   
        return;
    }

    int f[N][2];
    int ans = 0;

    void dp(int u, int fa)
    {
        for (int v : e[u])
        {
            if (v == fa)
                continue;
            dp(v, u);
            f[u][1] = (1ll * f[u][1] * ((f[v][1] + (f[v][0] << 1) % mod) % mod) % mod + 1ll * f[u][0] * f[v][1] % mod) % mod;
            f[u][0] = 1ll * f[u][0] * ((f[v][0] << 1) % mod) % mod;
        }
        if (!(u ^ 1))
            ans = (ans + f[u][1]) % mod;
        else
            ans = (ans + 1ll * f[u][1] * qpow(2, s[1] - s[u] - 1) % mod) % mod;
        return;
    }

public:
    inline void calculate()
    {

        Tarjan(1, -1);

        for (int i = 1; i <= n; ++i)
            for (int j : g[i])
            {
                if (c[i] != c[j])
                    e[c[i]].push_back(c[j]);
                else
                    ecnt[c[i]]++;
            }

        for (int i = 1; i <= sccnt; ++i)
        {
            ecnt[i] >>= 1;
            f[i][0] = qpow(2, ecnt[i]);
            f[i][1] = (qpow(2, sz[i] + ecnt[i]) - f[i][0] + mod) % mod;
        }
        dfs(1, -1);
        dp(1, -1);

        cout << ans << '\n';

        return;
    }

} sol;

inline void solve()
{
    init();
    sol.calculate();
    return;
}

signed main()
{
    cin.tie(nullptr)->ios::sync_with_stdio(false);
    solve();
    return 0;
}