强连通分量

参考

这一篇讲的真的非常详细!

强连通分量

引入

强连通的定义: 有向图 G 强连通指的是 G 中任意两个节点都可以互相到达.

强连通分量 (SCC) 的定义是: 极大的强连通子图.

举个栗子, 下图为一个有向图.

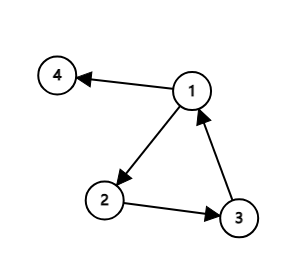
在这个图中, 1, 2 两点可以互相到达对方, 所以这两个点强连通.

而1, 2 和 3 中任意两个点都可以互达, 所以它们是整个有向图的强连通分量.

Tarjan 求强连通分量

还是这篇博客!

里面的图示 & 解释均十分详细, 这里就不过多赘述了qwq.

真的一遍就能看懂!

模板

void Tarjan(int u)
{
    lw[u] = dfn[u] = ++cnt;
    s.push(u), vis[u] = 1;
    for (int v : g[u])
    {
        if (!dfn[v])
            Tarjan(v), lw[u] = min(lw[u], lw[v]);
        else if (vis[v])
            lw[u] = min(lw[u], dfn[v]);
    }
    if (!(dfn[u] ^ lw[u]))
    {
        int t = -1;
        sccnt++;
        while (t ^ u)
        {
            t = s.top(), s.pop();
            vis[t] = 0, c[t] = sccnt;
        }
    }
    return;
}

因为从一个点出发不一定能到达所有点, 所以我们需要在主函数内多次调用.

具体地, 如果一个点还没有 dfs 序, 那么说明它没有被遍历过, 就从这个点开是跑 Tarjan.

缩点

定义

将每个强连通分量看作一个大点, 保留不在强连通分量内部的边, 这样的图就是缩点后的图.

因为缩完点后的图只保留了不在分量内的边, 所以所成的图一定是一个 DAG, 可以进行拓扑排序.