格与布尔代数
思维导图
回顾

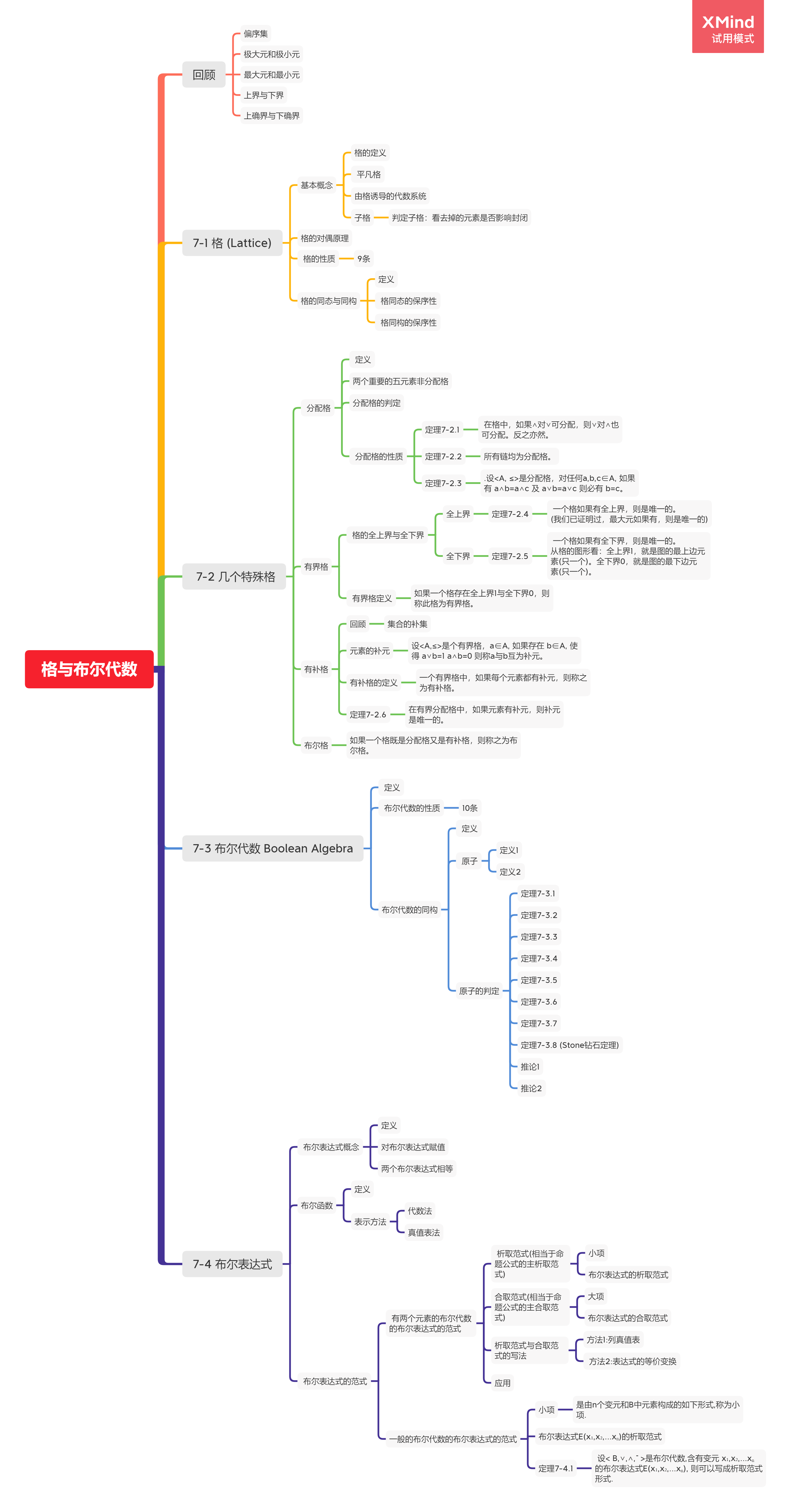
偏序集

极大元和极小元
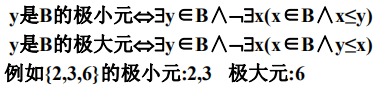
最大元和最小元

上界与下界

上确界与下确界

7-1 格 (Lattice)
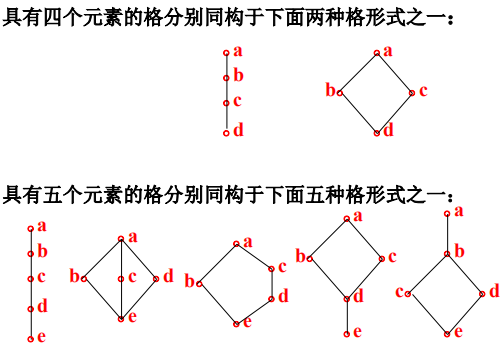
基本概念
-
格的定义
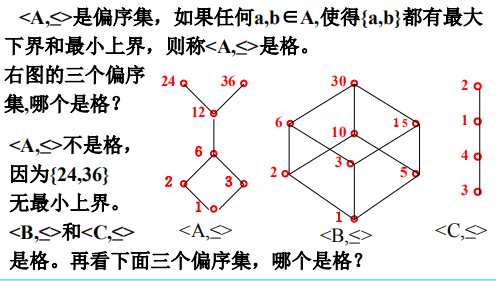
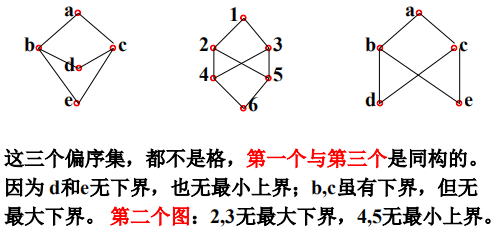
-
平凡格

-
由格诱导的代数系统

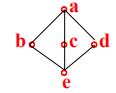
-
子格
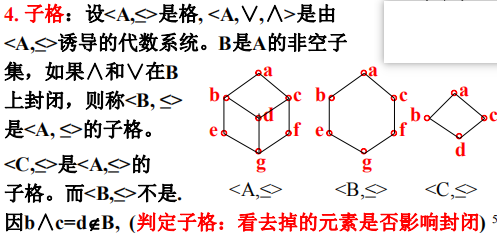
- 判定子格:看去掉的元素是否影响封闭
格的对偶原理

格的性质
- 9条





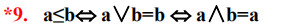
格的同态与同构
-
定义


-
格同态的保序性

-
格同构的保序性


7-2 几个特殊格
分配格
-
定义

-
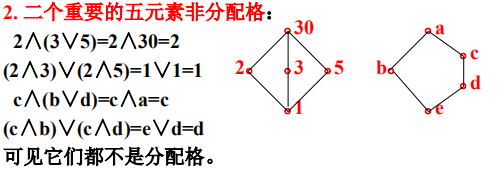
两个重要的五元素非分配格
-
分配格的判定

-
分配格的性质
-
定理7-2.1
- 在格中,如果∧对∨可分配,则∨对∧也
可分配。反之亦然。

- 在格中,如果∧对∨可分配,则∨对∧也
-
定理7-2.2
- 所有链均为分配格。

- 所有链均为分配格。
-
定理7-2.3
- 设<A, ≤>是分配格,对任何a,b,c∈A, 如果
有 a∧b=a∧c 及 a∨b=a∨c 则必有 b=c。

- 设<A, ≤>是分配格,对任何a,b,c∈A, 如果
-
有界格
-
格的全上界与全下界
-
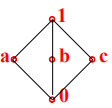
全上界


-
定理7-2.4
- 一个格如果有全上界,则是唯一的。
(我们已证明过,最大元如果有,则是唯一的)
- 一个格如果有全上界,则是唯一的。
-
-
全下界

-
定理7-2.5
- 一个格如果有全下界,则是唯一的。
从格的图形看:全上界1,就是图的最上边元素(只一个)。全下界0,就是图的最下边元素(只一个)。
- 一个格如果有全下界,则是唯一的。
-
-
-
有界格定义
- 如果一个格存在全上界1与全下界0,则
称此格为有界格。

- 如果一个格存在全上界1与全下界0,则
有补格
-
回顾
- 集合的补集
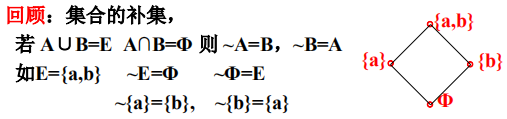
- 集合的补集
-
元素的补元
- 设<A,≤>是个有界格,a∈A, 如果存在 b∈A, 使得 a∨b=1 a∧b=0 则称a与b互为补元。

- 设<A,≤>是个有界格,a∈A, 如果存在 b∈A, 使得 a∨b=1 a∧b=0 则称a与b互为补元。
-
有补格的定义
- 一个有界格中,如果每个元素都有补元,则称之为有补格。
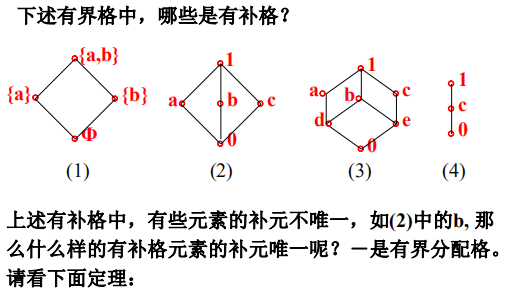
- 一个有界格中,如果每个元素都有补元,则称之为有补格。
-
定理7-2.6
- 在有界分配格中,如果元素有补元,则补元
是唯一的。

- 在有界分配格中,如果元素有补元,则补元
布尔格
- 如果一个格既是分配格又是有补格,则称之为布尔格。

7-3 布尔代数 Boolean Algebra
定义

布尔代数的性质
- 10条


布尔代数的同构
-
定义

-
原子
-
定义1

-
定义2
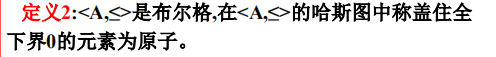
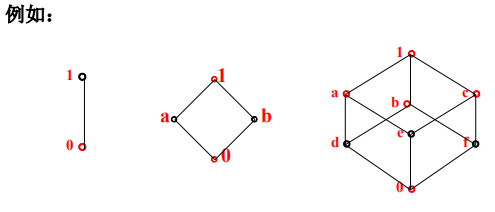
-
-
原子的判定
-
定理7-3.1

-
定理7-3.2
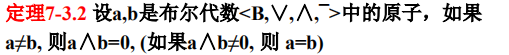
-
定理7-3.3

-
定理7-3.4
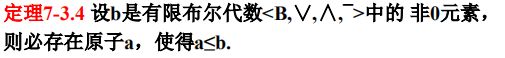
-
定理7-3.5
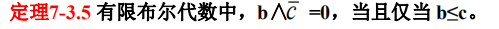
-
定理7-3.6

-
定理7-3.7
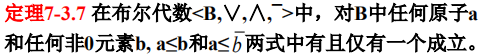
-
定理7-3.8 (Stone钻石定理)

-
推论1

-
推论2

-
7-4 布尔表达式
布尔表达式概念
-
定义

-
对布尔表达式赋值

-
两个布尔表达式相等

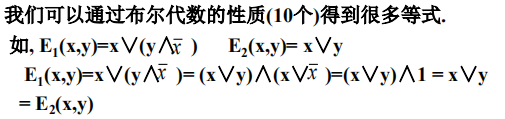
布尔函数
-
定义

-
表示方法
-
代数法
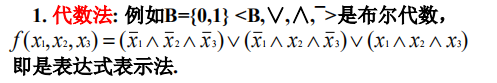
-
真值表法
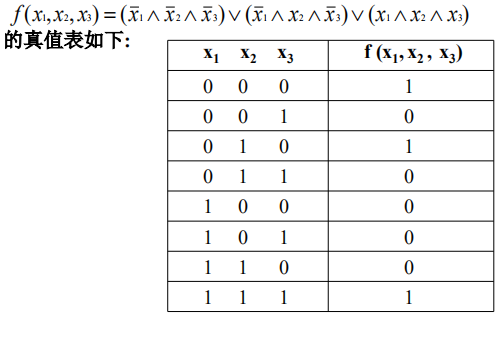
-
布尔表达式的范式
-
有两个元素的布尔代数的布尔表达式的范式

-
析取范式(相当于命题公式的主析取范式)
-
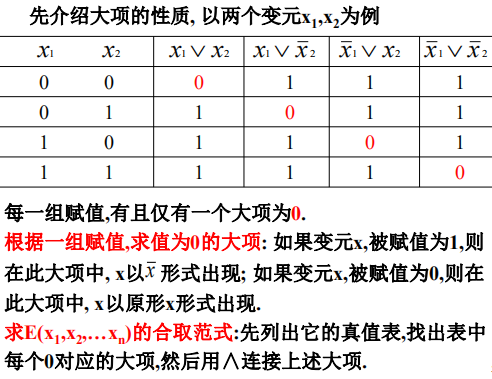
小项

-
布尔表达式的析取范式

-
-
合取范式(相当于命题公式的主合取范式)
-
大项

-
布尔表达式的合取范式

-
-
析取范式与合取范式的写法
-
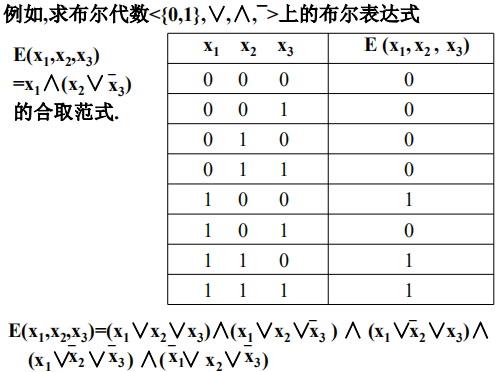
方法1:列真值表
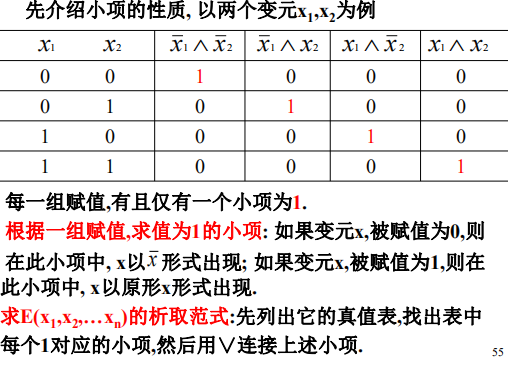
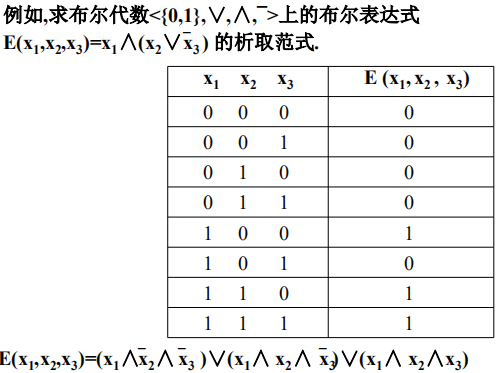
-
方法2:表达式的等价变换

-
-
应用
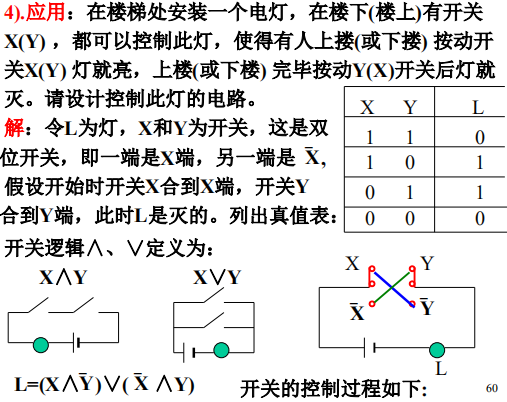
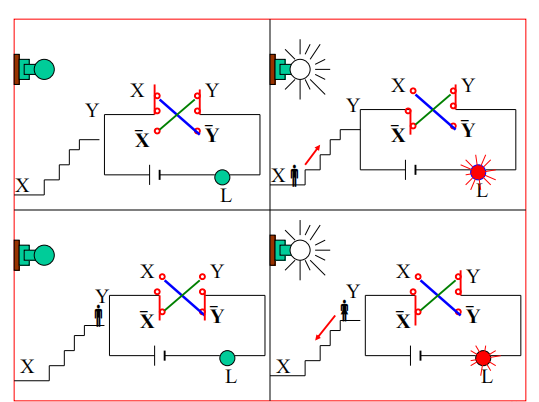
-
-
一般的布尔代数的布尔表达式的范式
-
小项
- 是由n个变元和B中元素构成的如下形式,称为小
项.
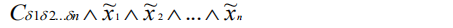

- 是由n个变元和B中元素构成的如下形式,称为小
-
布尔表达式E(x₁,x₂,...xₙ)的析取范式

-
定理7-4.1
- 设< B,∨,∧,¯>是布尔代数,含有变元 x₁,x₂,...xₙ
的布尔表达式E(x₁,x₂,...xₙ), 则可以写成析取范式形式.



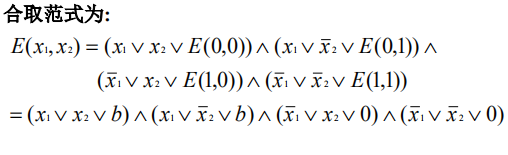
- 设< B,∨,∧,¯>是布尔代数,含有变元 x₁,x₂,...xₙ
-


 浙公网安备 33010602011771号
浙公网安备 33010602011771号