深度学习入门-基于Python的理论与实现(鱼书)学习笔记-Chapter3-神经网络

Chapter 3. 神经网络

3.1 从感知机到神经网络

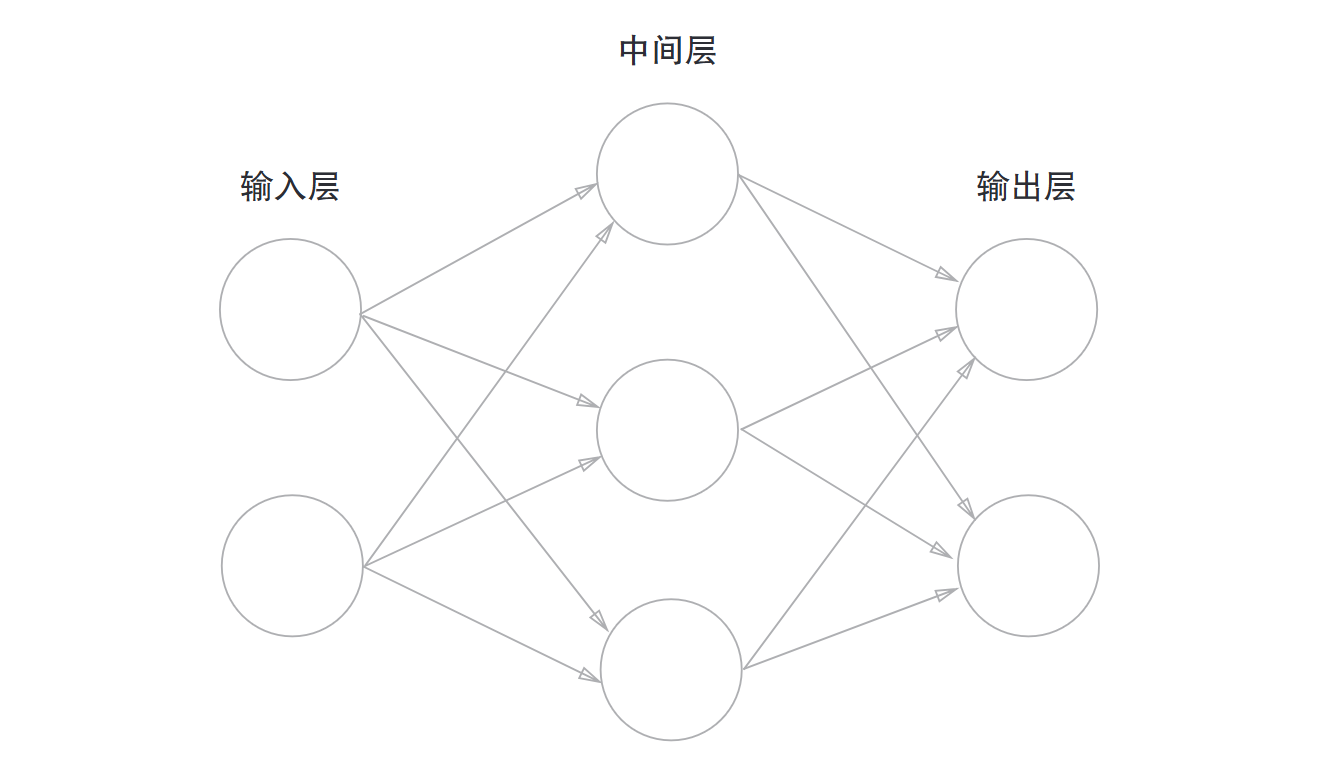
神经网络分为三层：输入层, 中间层(也称隐藏层), 输出层

)

实例中的网络一共有三层，但是只有两层有权重，所以也成为两层网络, 但是有的书也看层数将其成为三层网络

接下来观察一个感知机

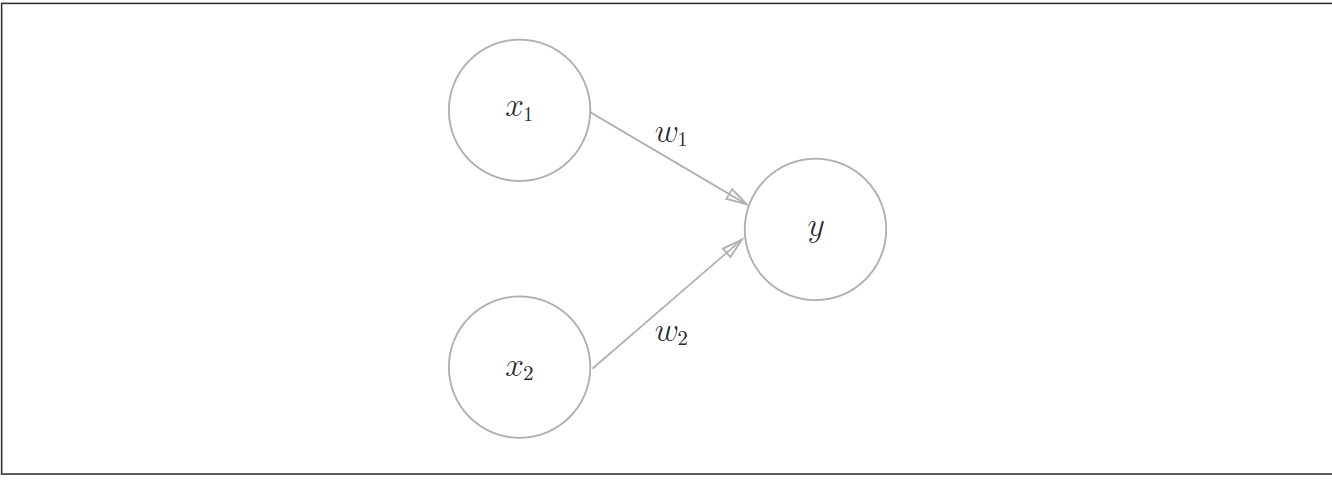
当然这里偏置b没有表现出来，也可以把偏置b当成一个信号恒为1, 权重为b的神经元

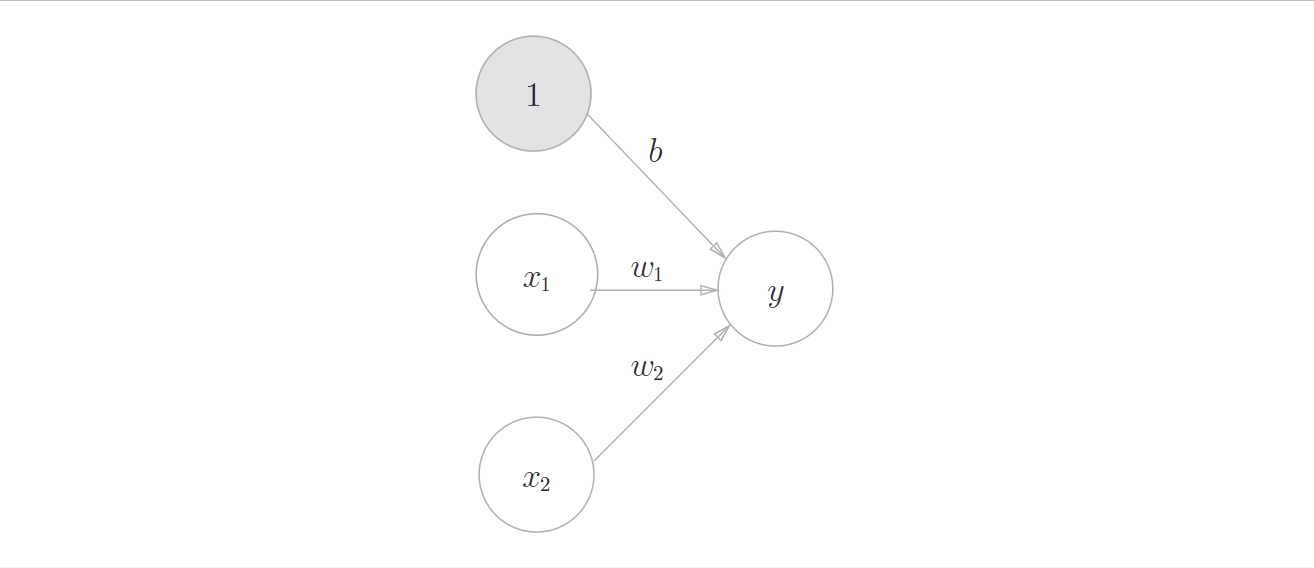
用数学式表示

\[y = \begin{cases} 0 & (b + w_1x_1 + w_2x_2 \leq 0)\\ 1 & (b + x_1x_1 + w_2x_2 > 0) \end{cases} \]

可以写得更简洁一些

\[y = h(b + w_1x_1 + w_2x_2) \]

\[h(x) = \begin{cases} 0 & x \leq 0\\ 1 & x > 0 \end{cases} \]

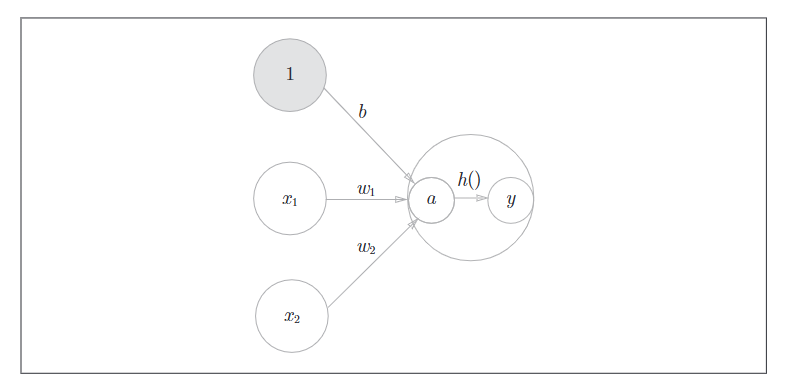
引出激活函数
刚刚的\(h(x)\)将输入信号的总和转换为输出信号，这样的函数称为激活函数，作用是决定如何来激活输入信号的总和

3.2 激活函数

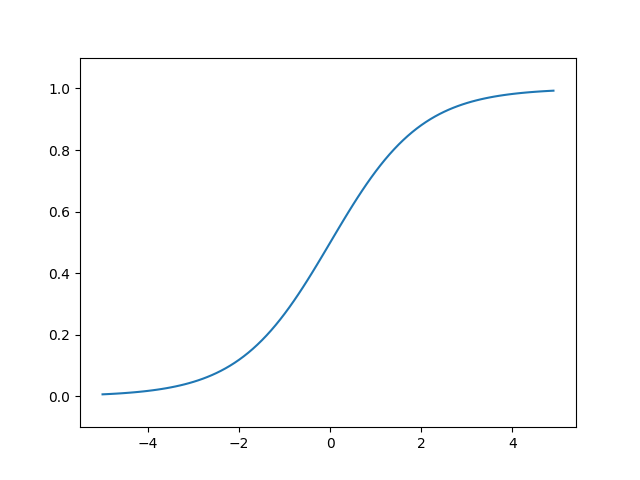
3.2.1 sigmoid函数

\[h(x) = \frac{1}{1 + e^{-x}} \]

def sigmoid(x):
    return 1.0 / (1 + numpy.exp(-x))

)

3.2.2 阶跃函数

def step_function(x):
    if (x > 0):
        return 1
    else:
        return 0

为了方便后面的操作，可以把它修改成为支持Numpy数组的实现

def step_function(x):
    y = x > 0
    return y.astype(np.int64)

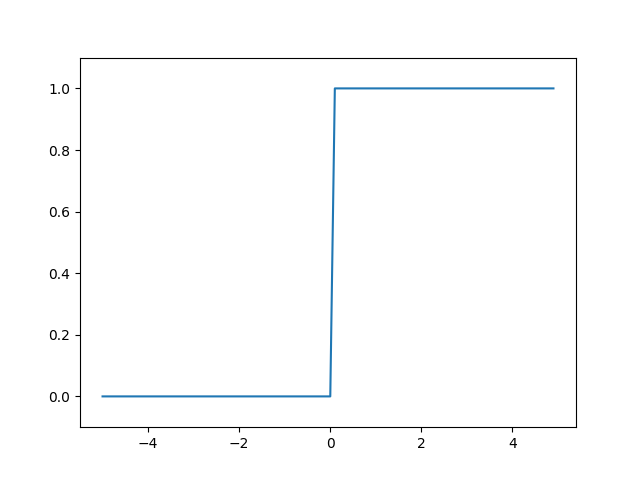
注意 阶跃函数和sigmoid函数都是非线性函数，神经网络的激活函数必须使用非线性函数，使用线性函数的缺点在于:不管如何加深层数，总是存在与之等效的"无隐藏层的神经网络"， 这样的话加深神经网络层数就没有意义了

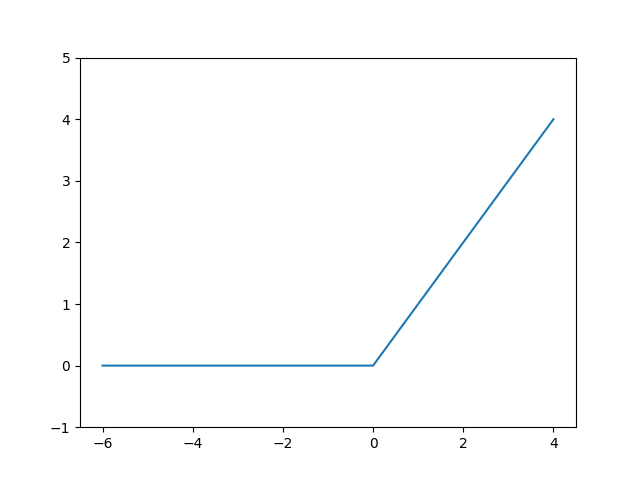
3.2.3 ReLU函数

\[h(x) = \begin{cases} x & (x > 0)\\ 0 & (x \leq 0) \end{cases} \]

def relu(x):
    return np.maximum(0, x)

3.3 多维数组的运算

3.3.1 多维数组

np.dim() 返回数组的维数
np.shape返回数组的形状，类型为tuple

3.3.2 矩阵乘法

这里主要是线性代数的知识

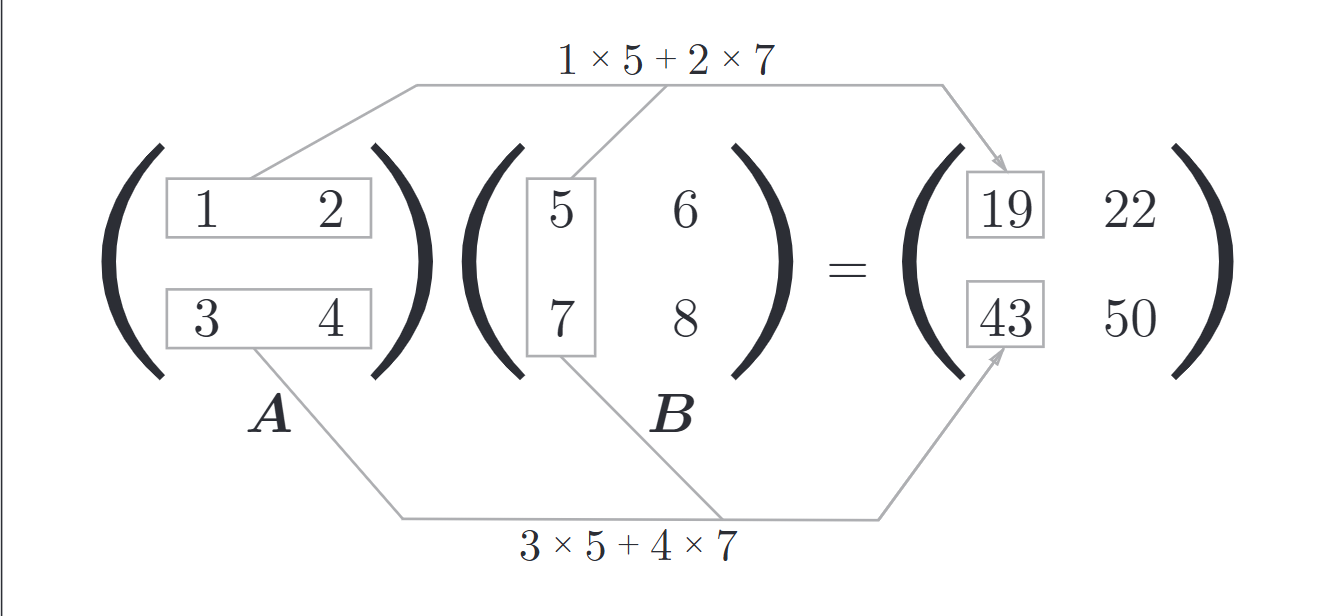
Numpy中的矩阵乘法

np.dot(matA, matB)

A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
C = np.dot(A, B)

注意
矩阵乘法和广播计算不同

3.3.3 神经网络的内积

X = np.array([1, 2])
W = np.array([[1, 3, 5], [2, 4, 6]])
Y = np.dot(X, W)

3.4 三层神经网络的实现

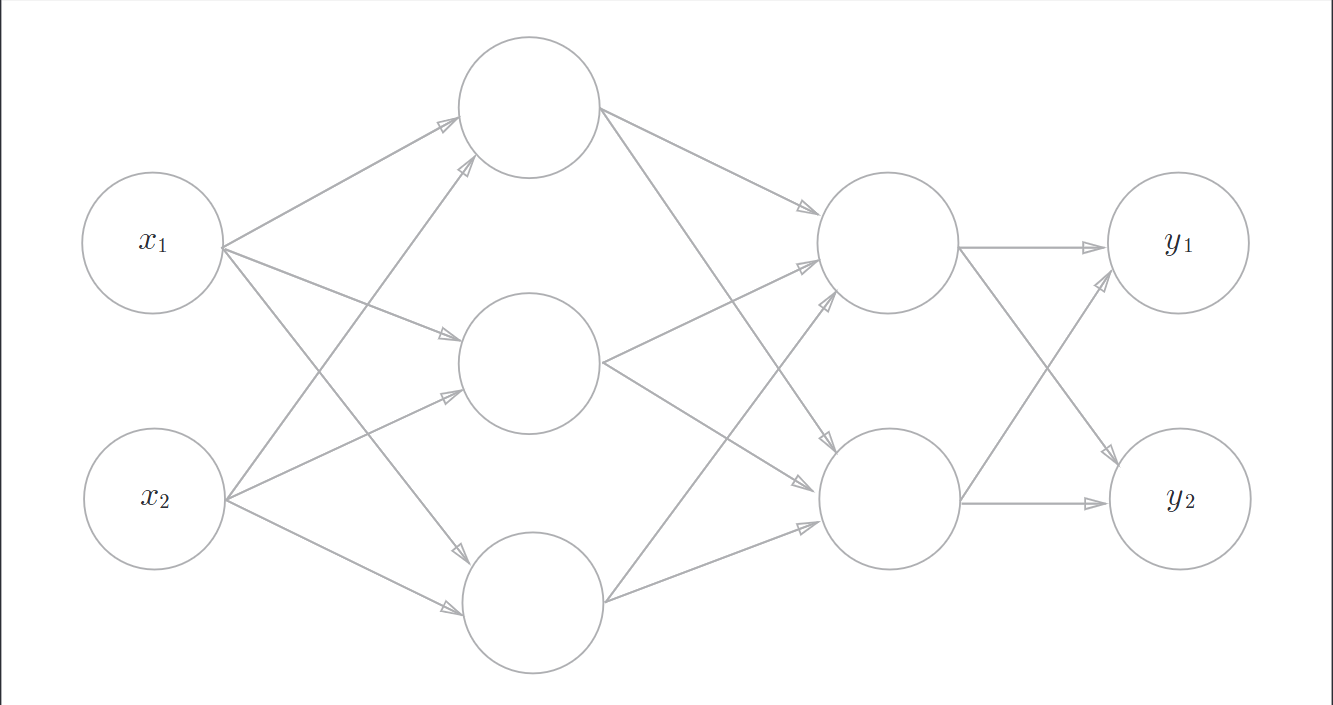
输入层(第0层)有2个神经元
第1个隐层层(第1层)有3个神经元
第2个隐藏层(第2层)有2个神经元
输出层(第3层)有2个神经元

一些符号的规定

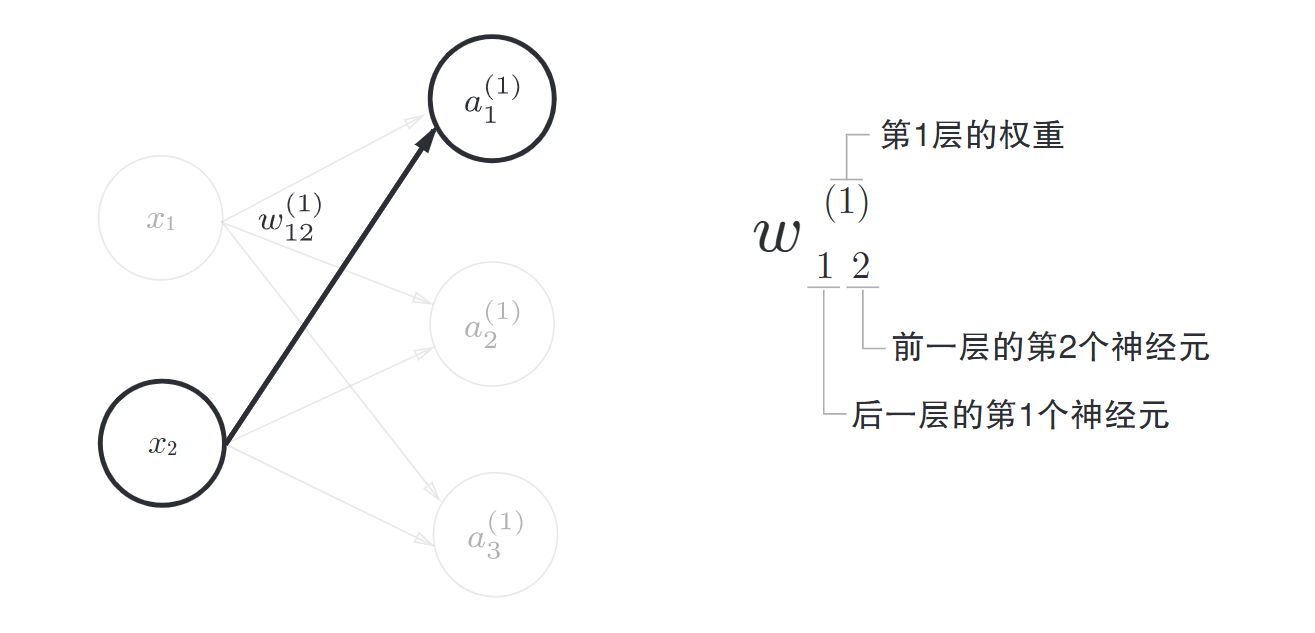
传递过程

\[{a_1}^{(1)} = {w_{11}}^{(1)}{x_1} + {w_{12}^{(1)}}{x_2} + {b_1}^{(1)}\\ {a_2}^{(1)} = {w_{21}}^{(1)}{x_2} + {w_{22}^{(1)}}{x_2} + {b_2}^{(1)}\\ {a_3}^{(1)} = {w_{31}}^{(1)}{x_3} + {w_{32}^{(1)}}{x_2} + {b_3}^{(1)} \]

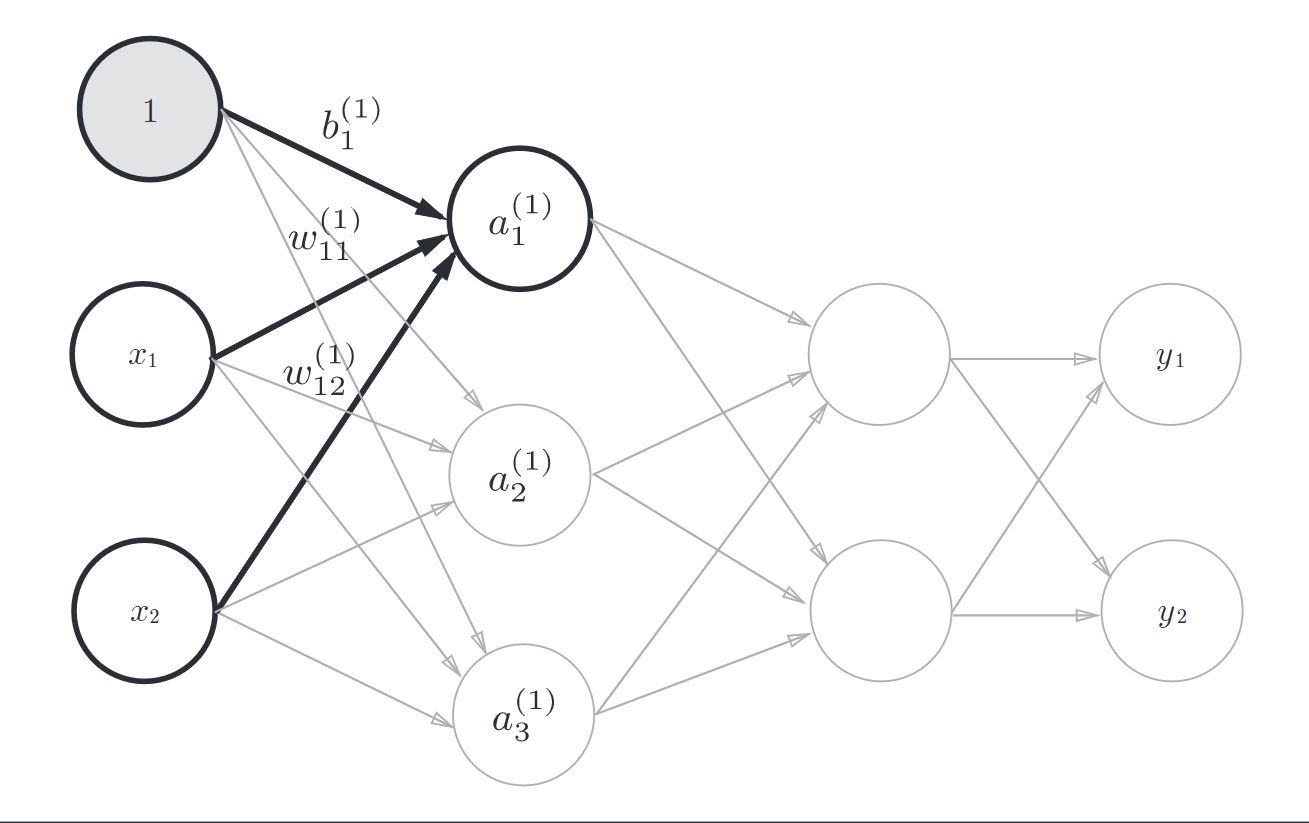
用矩阵表示就是

\[A^{(1)} = \begin{pmatrix} {a_1}^{(1)}, {a_2}^{(1)}, {a_3}^{(1)} \end{pmatrix} \]

\[X = \begin{pmatrix} x_1, x_2 \end{pmatrix} \]

\[W^{(1)} = \begin{pmatrix} {w_{11}}^{(1)}, {w_{21}}^{(1)}, {w_{31}}^{(1)}\\ {w_{12}}^{(1)}, {w_{22}}^{(1)}, {w_{32}}^{(1)} \end{pmatrix} \]

\[B^{(1)} = \begin{pmatrix} {b_1}^{(1)}, {b_2}^{(1)}, {b_3}^{(1)} \end{pmatrix} \]

然后就是这个式子

\[A^{(1)} = XW^{(1)} + B^{(1)} \]

X = np.array([1.0, 0.5])
W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
B1 = np.array([0.1, 0.2, 0.3])
A1 = np.dot(X, W1) + B1

之后再加上激活函数sigmoid可以实现从输入层到第1层的传递

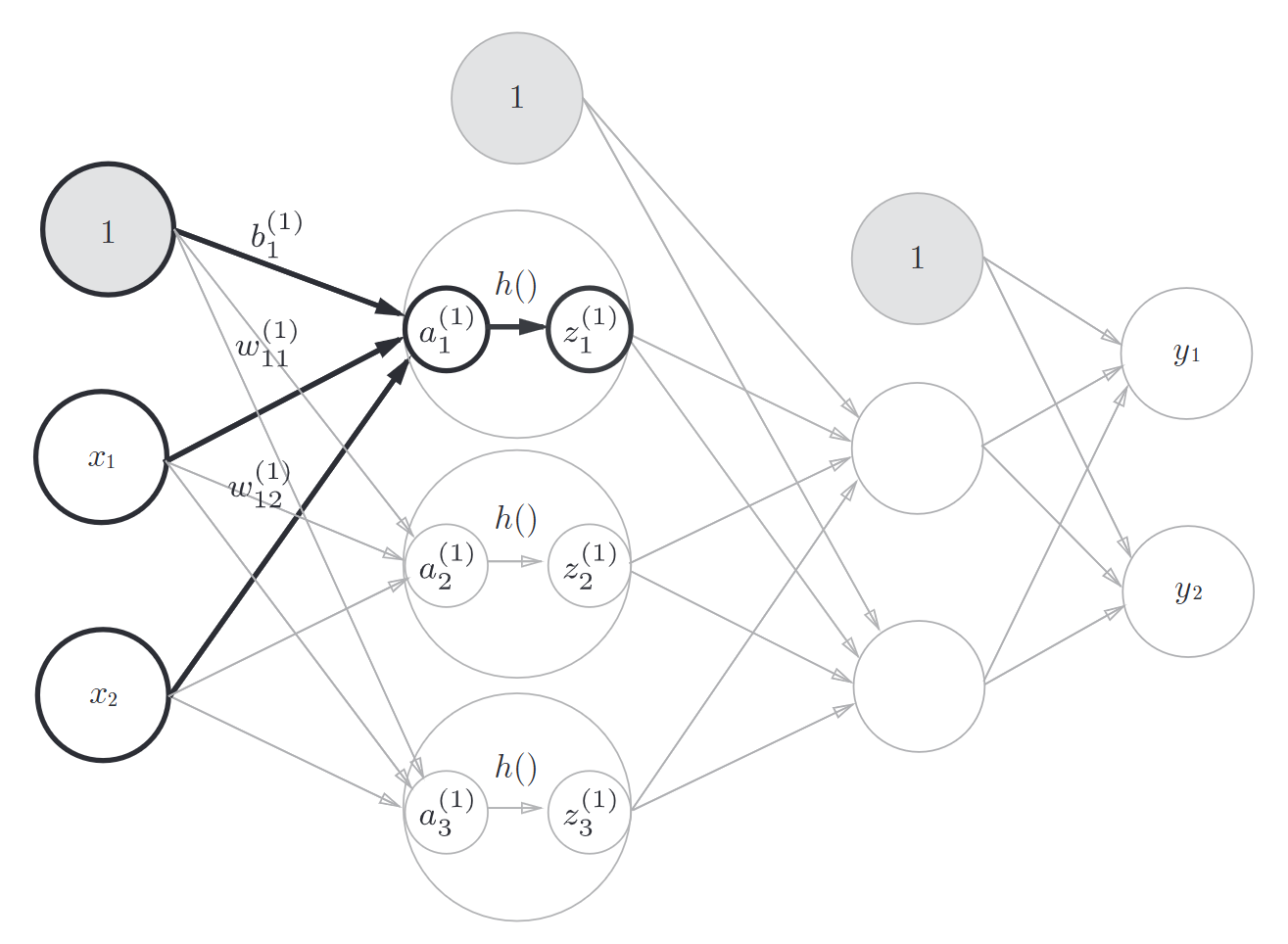
Z1 = sigmoid(A1)

接着实现从第1层到第2层的传递

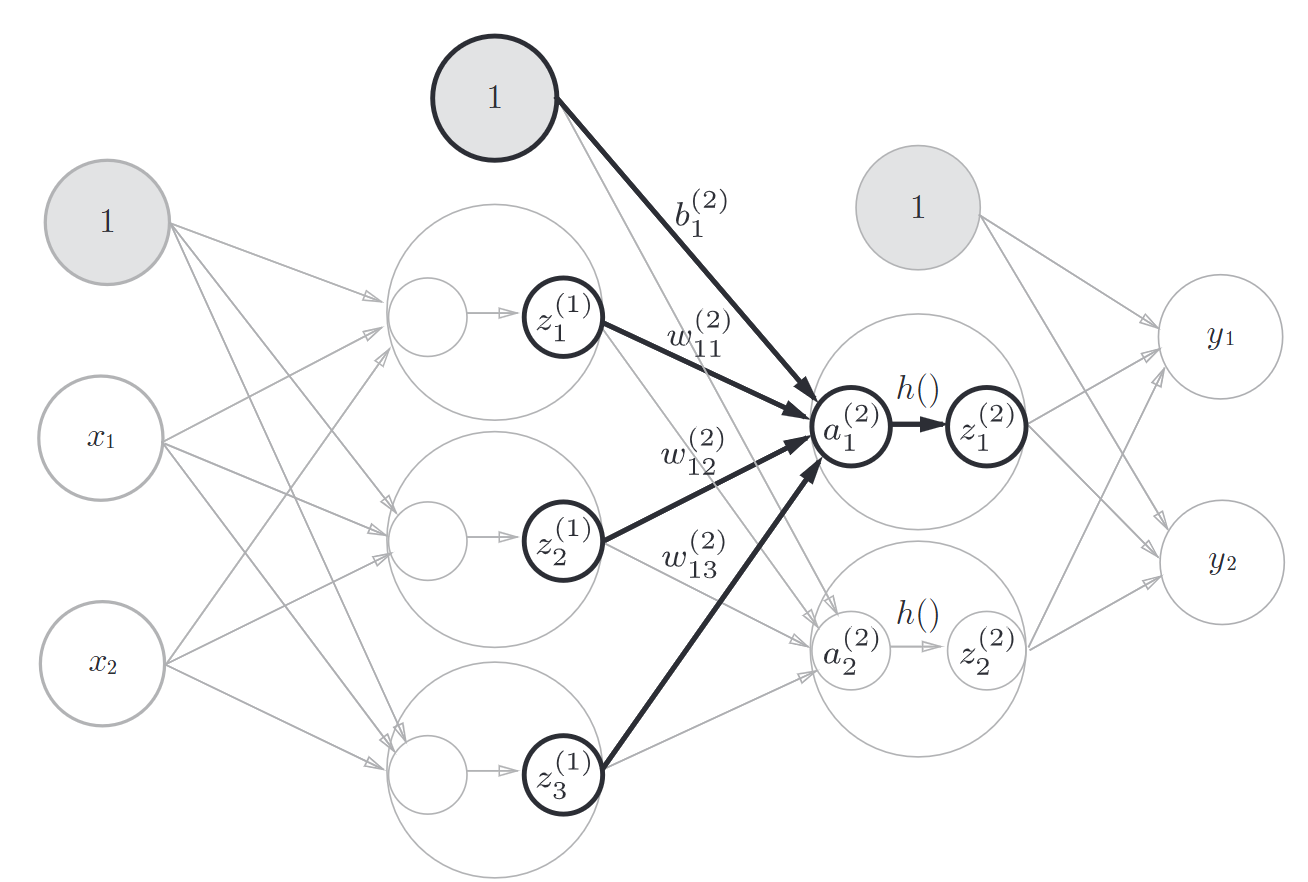
W2 = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
B2 = np.array([0.1, 0.2])
A2 = np.dot(Z1, W2) + B2
Z2 = sigmoid(A2)

最后是从第2层到输出层的传递， 这里激活函数有些不一样

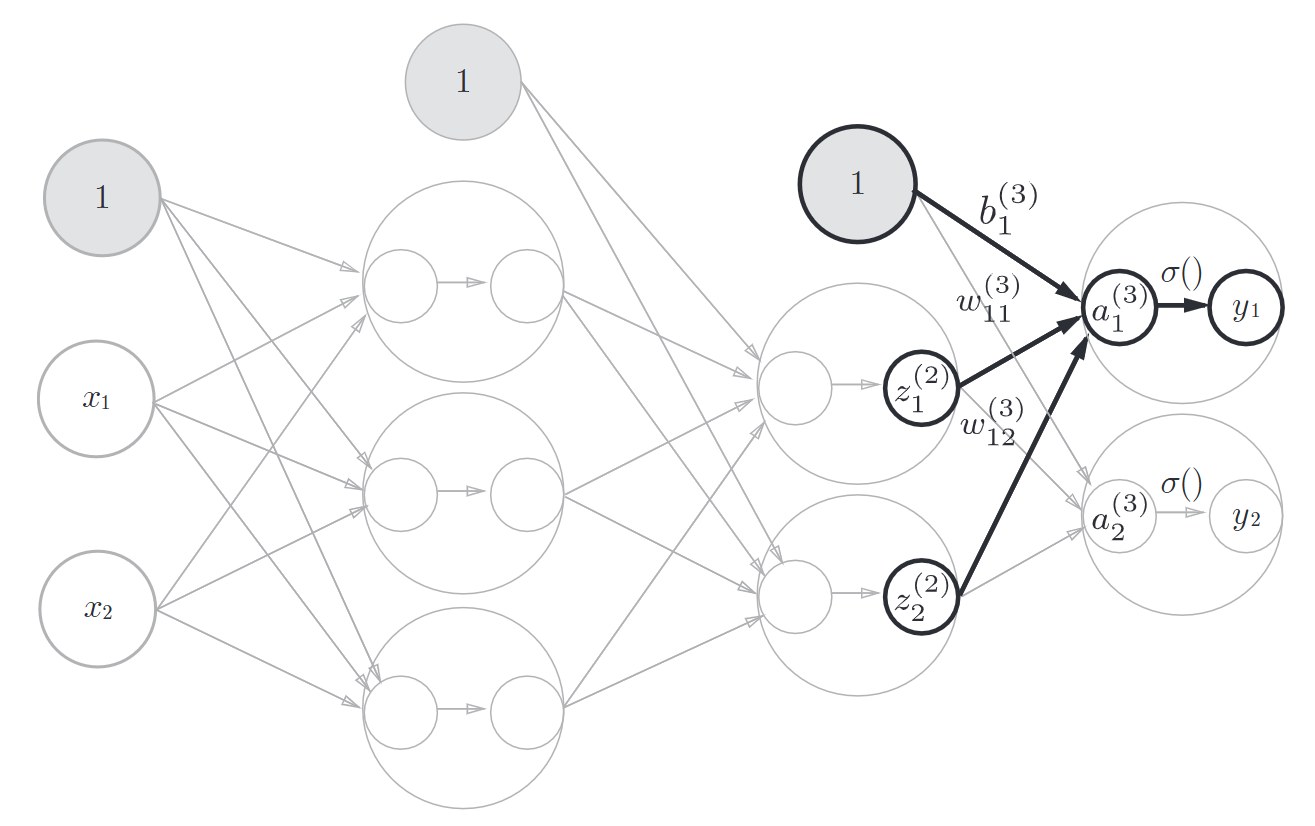
W3 = np.array([[0.1, 0.3], [0.2, 0.4]])
B3 = np.array([0.1, 0.2])

A3 = np.dot(Z2, W3) + B3
Y = identity_function(A3)

注意
一般地，回归问题可以使用恒等函数，二分类问题可以使用sigmoid函数，多元分类问题可以使用softmax函数

代码实现小结

3.5 输出层的设计

神经网络可以用在分类问题和回归问题上，不过需要根据情况改变输出层的激活函数

恒等函数
输入信号原封不动地被输出

def identify_function(x):
    return x

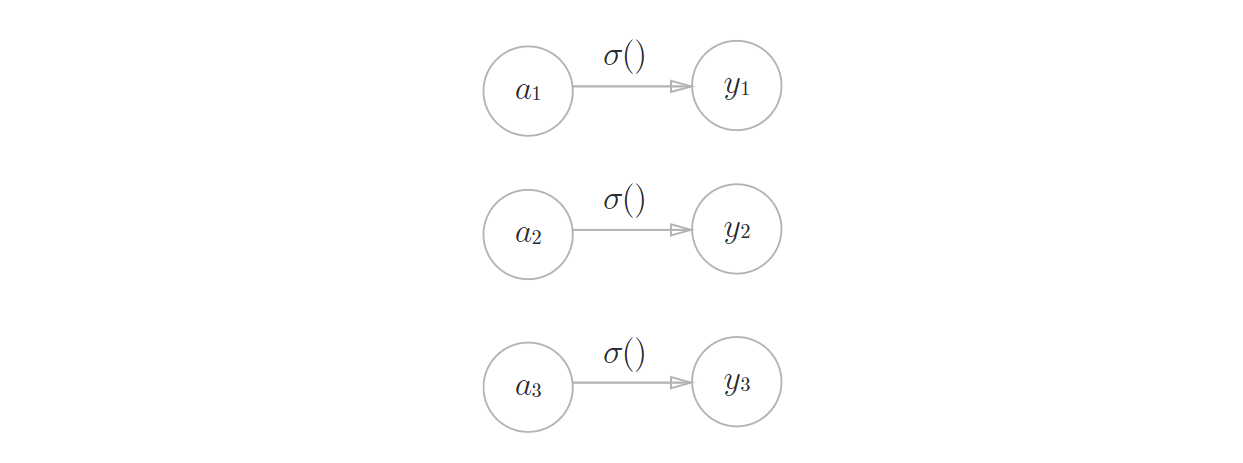
softmax函数

\[y_k = \frac{e^{a_k}}{\sum_{i = 1}^{n}e^{(a_i)}} \]

表示：假设输出层一共有n个神经元，计算第k个神经元的输出\(y_k\)，softmax函数的分子是输入信号\(a_k\)的指数函数，分母是所有输入信号的指数函数的和

def softmax(x):
    exp_x = np.exp(x)
    sum_exp_x = np.sum(exp_x)
    y = exp_x / sum_exp_x
    return y

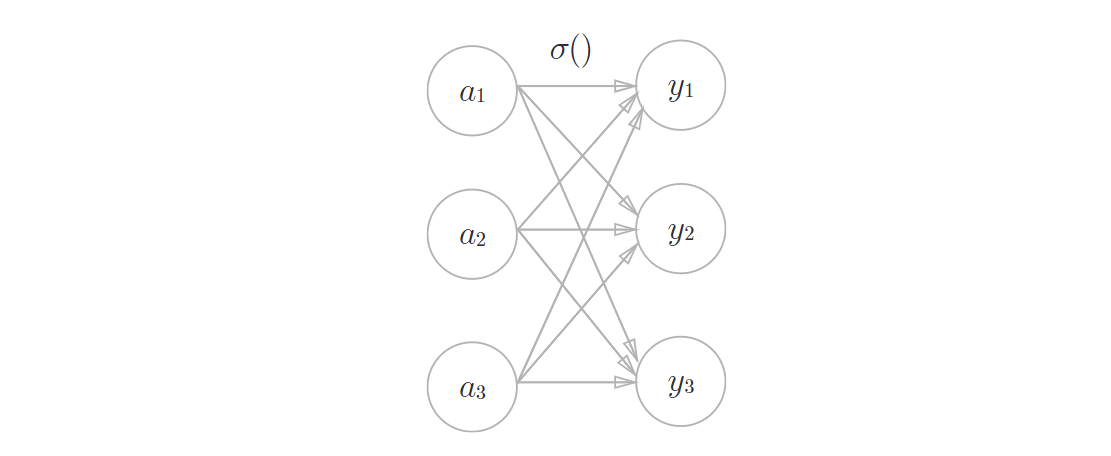
softmax函数需要注意的事

由于指数爆炸，所有数可能会非常打，所以要做一些变换

\[y_k = \frac{e^{a_k}}{\sum_{i = 1}^{n}e^{(a_i)}} = \frac{Ce^{a_k}}{C\sum_{i = 1}^{n}e^{(a_i)}} = \frac{e^{a_k + logC}}{\sum_{i = 1}^{n}e^{(a_i + logC)}} = \frac{e^{a_k + C^`}}{\sum_{i = 1}^{n}e^{(a_i + C^`)}} \]

def softmax(x):
    c = np.max(x)
    exp_x = np.exp(x)
    sum_exp_x = np.sum(exp_x)
    y = exp_x / sum_exp_x
    return y

softmax函数的特征

• 1- softmax函数总是输出0.0到1.0之间的实数
• 2 -softmax函数输出值的总和是1，所以才可以把softmax函数的输出解释为"概率"
• 3 -即使使用了softmax函数，各个元素之间的大小关系也不会改变

求解机器学习问题的步骤可以分为“学习”和“推理”两个阶段，首先，在学习阶段进行模型的学习，然后，在推理阶段，用学到的模型对未知的数据进行推理（分类）。推理阶段一般都会省略输出层的softmax函数。在输出层使用softmax函数是因为它和神经网络的学习有关

输出层的神经元的数量

输出层的神经元的数量需要根据待解决的问题来决定。对于分类问题，输出层的神经元数量一般设定为类别的数量