LeetCode每日一题-2025-8-27-LC3459.最长 V 形对角线段的长度

2025-08-27-LeetCode 每日一题 -3459.最长 V 形对角线段的长度

---

给你一个大小为 n x m 的二维整数矩阵 grid，其中每个元素的值为 0、1 或 2。

V 形对角线段 定义如下：

• 线段从 1 开始。
• 后续元素按照以下无限序列的模式排列：2, 0, 2, 0, ...。
• 该线段：
  • 起始于某个对角方向（左上到右下、右下到左上、右上到左下或左下到右上）。
  • 沿着相同的对角方向继续，保持  序列模式  。
  • 在保持  序列模式  的前提下，最多允许  一次顺时针 90 度转向  另一个对角方向。

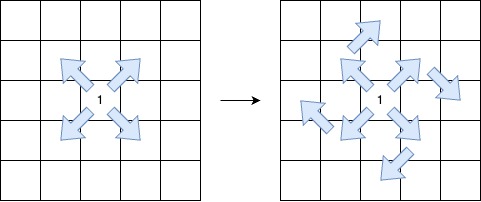
示例 1：

输入： grid = [[2,2,1,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2]]

输出： 5

解释：

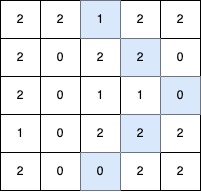
最长的 V 形对角线段长度为 5，路径如下：(0,2) → (1,3) → (2,4)，在 (2,4) 处进行  顺时针 90 度转向  ，继续路径为 (3,3) → (4,2)。

示例 2：

输入： grid = [[2,2,2,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2]]

输出： 4

解释：

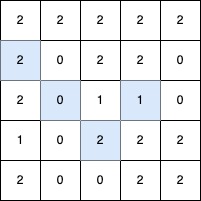
最长的 V 形对角线段长度为 4，路径如下：(2,3) → (3,2)，在 (3,2) 处进行  顺时针 90 度转向  ，继续路径为 (2,1) → (1,0)。

示例 3：

输入： grid = [[1,2,2,2,2],[2,2,2,2,0],[2,0,0,0,0],[0,0,2,2,2],[2,0,0,2,0]]

输出： 5

解释：

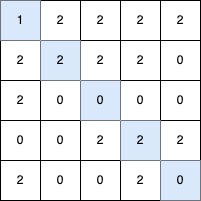
最长的 V 形对角线段长度为 5，路径如下：(0,0) → (1,1) → (2,2) → (3,3) → (4,4)。

示例 4：

输入： grid = [[1]]

输出： 1

解释：

最长的 V 形对角线段长度为 1，路径如下：(0,0)。

提示：

• n == grid.length
• m == grid[i].length
• 1 <= n, m <= 500
• grid[i][j] 的值为 0、1 或 2。

思路

记忆化搜索
\(dp[x][y][pos][flag]\)
\(pos\):
1 左下到右上
2 右下到左上
3 右上到左下
4 左上到右下

\(flag\)
0尚未转向
1已经转向

那么dp数组的含义就是在位置(x, y)时，朝向是pos时，已经/尚未转向时能走的最长距离

需要注意的点:

• 1. 从1开始
• 2. 2和0交替，所以需要记录上一位走的是什么
• 3. 及时剪枝

当flag == 1一直朝着当前的方向走下去就行

if (pos == 1) return dp[x][y][pos][flag] = 1 + search(search, x - 1, y + 1, 1, flag, nxt);
if (pos == 2) return dp[x][y][pos][flag] = 1 + search(search, x - 1, y - 1, 2, flag, nxt);
if (pos == 3) return dp[x][y][pos][flag] = 1 + search(search, x + 1, y - 1, 3, flag, nxt);
if (pos == 4) return dp[x][y][pos][flag] = 1 + search(search, x + 1, y + 1, 4, flag, nxt);

当flag == 0要么朝着当前方向走，要么转方向

int dx = 0, dy = 0, npos = 0;
if (pos == 1) dx = -1, dy = 1, npos = 4;
if (pos == 2) dx = -1, dy = -1, npos = 1;
if (pos == 3) dx = 1, dy = -1, npos = 2;
if (pos == 4) dx = 1, dy = 1, npos = 3;
int nx = dx + x, ny = dy + y;
// 要么继续走，要么转方向
return dp[x][y][pos][flag] = std::max(search(search, nx, ny, pos, flag, nxt) + 1, search(search, x, y, npos, 1, lst));

代码

const int dir[4][2] = {{-1, 0}, {1, 0}, {0, 1}, {0, -1}};

class Solution {
public:
    int lenOfVDiagonal(std::vector<std::vector<int>>& grid) 
    {
        int n = grid.size(), m = grid[0].size();
        std::vector<std::vector<int>> mat(n + 1, std::vector<int>(m + 1, -1));
        for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) mat[i][j] = grid[i - 1][j - 1];
        int dp[501][501][5][2] = {0};
        // 1 左下到右上
        // 2 右下到左上
        // 3 右上到左下
        // 4 左上到右下
        auto check = [&](int tx, int ty) -> bool
        {
            return (tx <= n && tx >= 1 && ty <= m && ty >= 1);
        };
        auto search = [&](auto&& search, int x, int y, int pos, int flag, int lst) -> int
        {
            int nxt = 0;
            if (lst == 0) nxt = 2;if (!check(x, y)) return 0;
            if (mat[x][y] != nxt) return 0;
            
            if(dp[x][y][pos][flag]) return dp[x][y][pos][flag];
            if (flag)
            {
                if (pos == 1) return dp[x][y][pos][flag] = 1 + search(search, x - 1, y + 1, 1, flag, nxt);
                if (pos == 2) return dp[x][y][pos][flag] = 1 + search(search, x - 1, y - 1, 2, flag, nxt);
                if (pos == 3) return dp[x][y][pos][flag] = 1 + search(search, x + 1, y - 1, 3, flag, nxt);
                if (pos == 4) return dp[x][y][pos][flag] = 1 + search(search, x + 1, y + 1, 4, flag, nxt);
            }
            else
            {
                int dx = 0, dy = 0, npos = 0;
                if (pos == 1) dx = -1, dy = 1, npos = 4;
                if (pos == 2) dx = -1, dy = -1, npos = 1;
                if (pos == 3) dx = 1, dy = -1, npos = 2;
                if (pos == 4) dx = 1, dy = 1, npos = 3;
                int nx = dx + x, ny = dy + y;

                // 要么继续走，要么转方向
                return dp[x][y][pos][flag] = std::max(search(search, nx, ny, pos, flag, nxt) + 1, search(search, x, y, npos, 1, lst));
            }
            return 0;
        }; 
        int ans = 0;
        for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) if (mat[i][j] == 1)
        {
            ans = std::max(1, ans);
            if (check(i - 1, j - 1) && mat[i - 1][j - 1] == 2) ans = std::max(ans, 1 + search(search, i - 1, j - 1, 2, 0, 0));
            if (check(i + 1, j + 1) && mat[i + 1][j + 1] == 2) ans = std::max(ans, 1 + search(search, i + 1, j + 1, 4, 0, 0));
            if (check(i - 1, j + 1) && mat[i - 1][j + 1] == 2) ans = std::max(ans, 1 + search(search, i - 1, j + 1, 1, 0, 0));
            if (check(i + 1, j - 1) && mat[i + 1][j - 1] == 2) ans = std::max(ans, 1 + search(search, i + 1, j - 1, 3, 0, 0));
        }
        return ans;
        // std::cout << search(search, 4, 3, 3, 0, 0) << '\n';
    }
};