摸你腮总结/杂题乱刷

模拟赛

证明自己在 AFO 的前几个月挣扎过。

NOIP Round 2

0+45+15+0=60，T1 挂了 50，原地 AFO。

---

T1

给定一个排列 \(a_i=i\)，最多互换 \(k\) 次，求操作后 $\sum a_i \oplus i $ 的最大值。

\(n,k \le 10^9\)。

无敌了，我赛时竟然不会。

显然最优情况只会互换一次，然后就不动了。

可以发现 \(2^m\) 与 \(2^m-1\) 异或最大，\(2^m+1\) 与 \(2^m-2\) 异或最大，依次类推，而且这些结果都是相同的。因此可以从 \(n\) 开始找到能跟她异或最大的那个，然后计算答案，更新 \(n\) 的值递归下去就行了。时间复杂度 \(O(\log n)\)。

注意特判 \(n = 2^m-1\) 的情况，因为此时与 \(0\) 异或最大。

点击查看代码

#include <iostream>
using namespace std;
#define ll long long
ll ans=0;
void sol(int x,int k){
	int c=-1,p=x;
	while(p) ++c,p>>=1;
	if((1<<(c+1))-1==x) --x;
	int s=1<<c;
	int tmp=min(x-s+1,k);
	ans+=2ll*tmp*((1<<(c+1))-1);
	k-=tmp,x-=2*tmp;
	if(k>0 && x>1) sol(x,k);
}
int main(){
	int T; scanf("%d",&T);
	while(T--){
		ans=0;
		int n,k; scanf("%d%d",&n,&k);
		sol(n,k);
		printf("%lld\n",ans);
	}
}

---

T2

算了不想说题意了。

md 模拟赛一开始怎么吃的兔子就想错了，然后按照错的方法还打了 45 分。

令 \(d_i\) 表示体积为 \(i\) 的兔子数量，那么留下的兔子数量就是所有连续不为 \(0\) 的 \(d\) 的最后一个数的和。就要让这些剩下的兔子尽可能多。

显然如果要操作就把 \(d_i\) 全部变成 \(0\)，要不然没意义。

加的操作一定比减的操作不优，因为加是把这些加到开头，产生 \(d_{i-1}-d_i\) 的贡献，而减就是加到末尾，产生 \(d_{i-1}+d_{i}-d_i=d_{i-1}\) 的贡献。

而且如果要把体积为 \(i\) 的全部减去，那么 \(i-1\) 一定不操作。

然后呢？dp 呗。

\(f_i\) 表示只考虑前 \(i\) 个的最大贡献。

\(f_i \gets \max (f_{i-1} , f_{i-2}+d_{i-1})\)。

假设体积最大的是 \(m\)，那么 dp 要枚举到 \(m+1\)，答案就是 \(n-f_{m+1}\)。

点击查看代码

#include <iostream>
using namespace std;
const int N=1e5+5;
int n,maxn=0,d[N],dp[N];
int main(){
//	freopen("bunny4.in","r",stdin);
	
	scanf("%d",&n);
	for(int i=1;i<=n;++i){
		int x; scanf("%d",&x);
		d[x]++;
		maxn=max(maxn,x);
	}
	for(int i=2;i<=maxn+1;++i)
		dp[i]=max(dp[i-1],dp[i-2]+d[i-1]);
	printf("%d\n",n-dp[maxn+1]);
}

---

CSP Round 2

T2

贪心：大的必定都放一起，小的必定都放一起，否则一定不优。

反思：赛时没想到，糖丸。

就是把排序后的序列分层三份，假设最大的在第一组，那么两种情况：\(231\)、\(321\)。

假设分层三份的两个断点是 \(i,t\)，那么第二份的 \(t\) 向右移动一定是劣的，所以可以枚举 \(i\)，让 \(t\) 尽可能小，再判断所有的是不是都合法。

点击查看代码

#include <stdio.h>
#include <algorithm>
using std::sort;
const int N=5e5+5;
struct node{
	int x,id;
	bool operator < (const node &other) const{
		return x<other.x;
	}
}a[N];
int n,ans[N];
void put(){
	printf("YES\n");
	for(int i=1;i<=n;++i) printf("%d ",ans[i]);
	printf("\n");
}
void sol(){
	scanf("%d",&n);
	for(int i=1;i<=n;++i) scanf("%d",&a[i].x),a[i].id=i;
	sort(a+1,a+n+1);
	int maxn=a[n].x;
	for(int i=maxn;i<n;++i){
		int t=i+a[i].x;
		if(t<n&&n-t>=a[t].x){
			for(int j=1;j<=i;++j) ans[a[j].id]=2;
			for(int j=i+1;j<=t;++j) ans[a[j].id]=3;
			for(int j=t+1;j<=n;++j) ans[a[j].id]=1;
			return put();
		}
	}
	for(int i=1;i<n;++i){
		int t=i+a[n].x;
		if(!(i<t&&t<n)) continue;
		if(n-t>=a[i].x&&i>=a[t].x){
			for(int j=1;j<=i;++j) ans[a[j].id]=3;
			for(int j=i+1;j<=t;++j) ans[a[j].id]=2;
			for(int j=t+1;j<=n;++j) ans[a[j].id]=1;
			return put();
		}
	}
	printf("NO\n");
}
int main(){
	int T; scanf("%d",&T);
	while(T--) sol();
}

---

T4

给定一棵有根树，点有点权（正数且不超过 \(10^5\)），每次询问是否存在一条链使得该链的点权之和恰好等于 \(k\)（\(k\le 10^5\)）

可以每个点维护一个集合 \(S_u\)，表示以这个点为链底时可以取到的所有答案，子节点的信息可以根据父节点推出来。

注意到每次询问的 \(k\) 不大，可以每个点开一个 bitset 作为维护的集合。为什么不能回溯？因为左移后自然溢出的部分没办法找到，即不可逆。

考虑优化空间，如果一个点的信息被所有的子节点都利用了，那么这个点的信息就没用了。所以考虑重链剖分，先让轻儿子利用，再扔给重儿子。注意每个轻儿子 dfs 完后也要把这个儿子的信息扔掉，因为没用。

因为任意一个点沿重链跳到根节点的复杂度不超过 \(\log n\)，所以只需要 \(\log n\) 个 bitset。

反思：如果需要子树内具体信息时，或者需要父节点的具体信息时，可以用轻重儿子的思想优化空间（或者 dsu on tree 或 线段树合并）

点击查看代码

#include <stdio.h>
#include <bitset>
#include <vector>
using namespace std;
const int N=1e5+5;
vector<int> e[N];
bitset<N> s[100],ans;
int son[N],siz[N],fa[N],pos[N],a[N];
int n,q,idx=1,rt;
void dfs1(int u){
	siz[u]=1;
	int maxson=-1;
	for(int v:e[u]){
		dfs1(v);
		siz[u]+=siz[v];
		if(siz[v]>maxson) maxson=siz[v],son[u]=v;
	}
}
void dfs(int u,int top){
	if(u==top) s[idx]=s[idx-1];
	s[idx]<<=a[u]; s[idx][a[u]]=1;
	ans|=s[idx];
	for(int v:e[u])
		if(v!=son[u]) ++idx,dfs(v,v),--idx;
	if(son[u]) dfs(son[u],top);
}
int main(){
	scanf("%d%d",&n,&q);
	for(int i=1;i<=n;++i){
		scanf("%d",&fa[i]);
		e[fa[i]].push_back(i);
		if(!fa[i]) rt=i;
	}
	for(int i=1;i<=n;++i) scanf("%d",&a[i]);
	dfs1(rt); dfs(rt,rt);
	while(q--){
		int x; scanf("%d",&x);
		puts(ans[x]?"YES":"NO");
	}
}

---

NOIP 20 Round 3

100+20+25+5=150，严格小于 frz 的 230，不活了。

T1

如果 \(x_i\) 和 \(x_j\) 从低位开始数的后 \(k\) 位都完全一样，那么得到的 \(y_i\) 和 \(y_j\) 的第 \(k\) 位也是一样的。

这就做完了。

赛时很久都没想出来，糖丸了。

点击查看代码

#include <stdio.h>
#include <vector>
#include <string.h>
using namespace std;
int n;
#define ri unsigned int
#define ull unsigned long long
const int N=3e5+5;
ri rd(){
	ri x=0;char ch=getchar();
	while(ch<'0'||ch>'9') ch=getchar();
	while(ch>='0'&&ch<='9'){x=x*(ri)10+(ri)ch-(ri)48;ch=getchar();}
	return x;
}
const int M=1e5+5;
struct HasH{
	int head[M],d[M],idx=0;
	vector<int> vec;
	struct Node{
		int nxt; 
		bool opt;
		ull key,value;  
	}list[N];
	int f(ull x){ return (x%(ull)M+M)%M;}
	bool get(ull k){
		for(int i=head[f(k)];i!=-1;i=list[i].nxt)
			if(k==list[i].key && list[i].opt) return 1;
		return 0;
	}
	ull find(ull k){
		for(int i=head[f(k)];i!=-1;i=list[i].nxt)
			if(k==list[i].key && list[i].opt) return list[i].value;
		return -1;
	}
	void add(ull k,ull v){
		int r=f(k);
		if(get(k)==1) return ;
		list[++idx]=(Node){head[r],1,k,v};
		head[r]=idx;
		if(!d[r]) d[r]=1,vec.push_back(r);
	}
	void update(ull k,ull v){
		for(int i=head[f(k)];i!=-1;i=list[i].nxt)
			if(k==list[i].key && list[i].opt){
				list[i].value=v;
				return ;
			}
	}
	void del(ull k){
		for(int i=head[f(k)];i!=-1;i=list[i].nxt)
			if(k==list[i].key){
				list[i].opt = 0;
				return ;
			}
	}
	void clen(){
		for(int p:vec) head[p]=-1,d[p]=0;
		vec.clear();
	}
	void init(){
		memset(head,-1,sizeof head);
		memset(d,0,sizeof d);
	}
}h[40];
ri x[N],y[N];
unordered_map<ri,int> mp[N];
#define b(x,y) ((x>>y)&(ri)1)
void sol(){
	scanf("%d",&n);
	for(int i=1;i<=n;++i) x[i]=rd(),y[i]=rd();
	for(int i=0;i<32;++i) h[i].clen();
	for(int i=1;i<=n;++i){
		int now=0;
		for(int t=0;t<32;++t){
			now+=(b(x[i],t)<<t);
			if(!h[t].get(now+1)){
				h[t].add(now+1,b(y[i],t));
			}
			ri op=h[t].find(now+1);
			if(op!=b(y[i],t))
				return void(puts("No"));
		}
	}
	puts("Yes");
}
int main(){
	freopen("hajimi.in","r",stdin);
	freopen("hajimi.out","w",stdout);
	for(int i=0;i<=31;++i) h[i].init();
	int _; scanf("%d",&_);
	while(_--) sol();
}

---

T2

dp 裸题，更是糖丸。

可以假设两堆是集合 \(A,B\)，令 \(A\) 的价值大于等于 \(B\) 的价值。

设状态 \(f_{i,j,t}\) 表示前 \(i\) 个中，\(\sum_{i \in A} a_i - \sum_{i \in B} a_i = j\) 时，且使用了 \(t\) 次机会的价值之和。

状态转移：

• 不选。
• 不使用机会且放到 \(A\) 中 ：\(f_{i,j,t} \leftarrow f_{i-1,j+a_i,t} + 2\times v_i\)。
• 使用机会且放到 \(A\) 中 ：\(f_{i,j,t} \leftarrow f_{i-1,j+2 \times a_i,t-1} + 2\times v_i\)。
• 不使用机会且放到 \(B\) 中 ：\(f_{i,j,t} \leftarrow f_{i-1,j-a_i,t} + v_i\)。
• 使用机会且放到 \(B\) 中 ：\(f_{i,j,t} \leftarrow f_{i-1,j-2 \times a_i,t-1} + v_i\)。

第一维显然可以滚动数组，时间复杂度 \(O(n^3 A),A=13\)。

像这种用两个集合的差值表示状态在 [CSP-S2019] Emiya 家今天的饭 中也出现过。

要注意初始化，否则容易 \(100 \rightarrow 30\)。

点击查看代码

#include <iostream>
using namespace std;
#define ll long long
const int N=3000;
ll dp[2][2*N+500][105];
int v[105],a[105];
int n,k;
void upd(ll &x,ll y){x=max(x,y);}
int main(){
	scanf("%d%d",&n,&k);
	for(int i=1;i<=n;++i) scanf("%d%d",&v[i],&a[i]);
	for(int j=0;j<=2*N+50;++j)
		for(int t=0;t<=k;++t) dp[0][j][t]=dp[1][j][t]=-1e17;
	dp[0][N][0]=0;
	for(int i=1;i<=n;++i){
		int op=i&1;
		for(int t=0;t<=k;++t){
			for(int j=0;j<=2*N;++j){
				upd(dp[op][j][t],dp[op^1][j][t]);
				if(j+a[i]>=0)
					upd(dp[op][j][t],dp[op^1][j+a[i]][t]+2ll*v[i]);
				if(j+2*a[i]>=0 && t)
					upd(dp[op][j][t],dp[op^1][j+2*a[i]][t-1]+2ll*v[i]);
				if(j-a[i]>=0)
					upd(dp[op][j][t],dp[op^1][j-a[i]][t]+v[i]);
				if(j-2*a[i]>=0 && t)
					upd(dp[op][j][t],dp[op^1][j-2*a[i]][t-1]+v[i]);
			}
		}
	}
	ll ans=0;
	for(int i=0;i<=k;++i) ans=max(ans,dp[n&1][N][i]);
	printf("%lld\n",ans);
}

---

NOIP 20 Round 4

蓝黑黑黑，zr 模拟赛还在发力。

T1

赛时糖丸了。

显然每次贪心删当前距离最小的一对一定不劣。

但是如果两个点的路径交叉，即一个点被一个点对包围且另一个没有被包围，那么这两个先删哪个都不劣势。（赛时没想到这个）

所以就可以对数组从左往右扫描线，如果出现相同的就可以直接删，这个过程树状数组维护。

反思：如果一种思路死磕想不出来，那么很可能漏了其他没有发现的性质。

点击查看代码

#include <stdio.h>
#define ll long long
#define lowbit(x) (x&(-x))
const int N=5e5+5;
int t[N*2],las[N],n;
void add(int x){for(;x<=2*n;x+=lowbit(x)) ++t[x];}
int query(int x){
	int r=0;
	for(;x;x-=lowbit(x)) r+=t[x];
	return r;
}
int main(){
	scanf("%d",&n);
	ll ans=0;
	for(int i=1,x;i<=2*n;++i){
		scanf("%d",&x);
		if(las[x]){
			ans+=i-query(i)-las[x]+query(las[x])-1;
			add(las[x]),add(i);
		}
		else las[x]=i;
	}
	printf("%lld\n",ans+n);
}

---

NOIP 20 Round 5

T1

显然要求 \(\prod p_i^{a_i} = \sum p_i \times b_i\)，且 \(a_i + b_i = n_i\) 的值。

发现 \(\sum p_i \times n_i\) 一定小于 \(10^{18}\)，那么所有的 \(\sum a_i\) 一定小于 \(64\)。

假设至少存在一种方案，那么选择了一个 \(a_i\)，左边的值一定会减少 \(p_i \times a_i\)。因为 \(p_i\) 小于 \(500\)，那么一种方案与 \(\sum p_i \times n_i\) 的差一定不会超过 \(500 \times 64\)。直接枚举这个差判断就行了。

点击查看代码

#include <stdio.h>
#define ll long long
const int N=105;
int p[N],cnt[N]; ll n[N];
int m;
void sol(){
	scanf("%d",&m);
	ll sum=0;
	for(int i=1;i<=m;++i)
		scanf("%d%lld",&p[i],&n[i]),sum+=1ll*p[i]*n[i];
	ll ans=-1;
	for(int i=1;i<=40000&&i<sum;++i){
		ll x=sum-i,tmp=0;
		int flg=1;
		for(int j=1;j<=m;++j){
			cnt[j]=0;
			while(x%(ll)p[j]==0) x/=(ll)p[j],cnt[j]++;
			if(cnt[j]>n[j]){
				flg=0; break;
			}
			tmp+=1ll*p[j]*(n[j]-cnt[j]);
		}
		if(!flg||x>1||tmp!=sum-i) continue;
		ans=sum-i;
		break;
	}
	printf("%lld\n",ans);
}
int main(){
	freopen("magic.in","r",stdin);
	freopen("magic.out","w",stdout);
	int T; scanf("%d",&T);
	while(T--) sol();
}

---

T2

每一种方案都等价于 \(A_a \equiv A_b + c \pmod d\)。

如果 \(d\) 是 \(p\) 的倍数，那么 \((a-b) \bmod d \bmod p = (a-b) \bmod p\)。

所以对每一个 \(d = 2^0,2^1,2^2,\cdots,2^{15}\) 和 \(d=-1\) 的都情况开一个带权并查集维护一下就行了。每次在小于等于 \(d\) 的并查集中加边就行了。要注意判 \(-1\) 的情况。

点击查看代码

#include <stdio.h>
const int N=5e5+5;
#define ll long long
int n,m,pos[N];
struct tree{
	int fa[N],d;
	ll dis[N];
	int find(int x){
		if(fa[x]==x) return x;
		int r=find(fa[x]);
		dis[x]+=dis[fa[x]];
		return fa[x]=r;
	}
	int check(int a,int b,int c){
		int x=find(a),y=find(b);
		if(x^y) return 1;
		if(d!=-1) return ((dis[a]-dis[b])%(ll)d+d)%d==c%d;
		else return dis[a]-dis[b]==c;
	}
	void merge(int a,int b,int c){
		int x=find(a),y=find(b);
		if(x==y) return ;
		fa[x]=y;
		if(d!=-1) dis[x]=(((ll)c-dis[a]+dis[b])%(ll)d+d)%d;
		else dis[x]=(ll)c-dis[a]+dis[b];
	}
}f[20];
int main(){
	scanf("%d%d",&n,&m);
	for(int i=0;i<=15;++i){
		pos[1<<i]=i;
		f[i].d=(1<<i);
		for(int j=1;j<=n;++j) f[i].fa[j]=j;
	}
	f[16].d=-1;
	for(int j=1;j<=n;++j) f[16].fa[j]=j;
	while(m--){
		int a,b,c,d;
		scanf("%d%d%d%d",&a,&b,&c,&d);
		if(d!=-1) d=pos[d];
		int flg=1;
		for(int i=0;i<=16;++i)
			if(d==-1||(d>=i&&i<16))
				flg&=f[i].check(a,b,c);
		printf("%d\n",flg);
		if(!flg) continue;
		for(int i=0;i<=16;++i)
			if(d==-1||(d>=i&&i<16))
				f[i].merge(a,b,c);
	}
}

---

NOIP 20 Round 7

T2

一个经典 trick：\(k=i\) 时的答案可以视为 \(k \le i\) 时的答案，或者删 \(w\) 次最多能删除多少个。

如果每个数开一个桶 \(cnt\) 记录每一个数出现的次数，把 \(cnt\) 从大往小排，一定呈一个阶梯状。

假设执行 \(X\) 次操作一和 \(Y\) 次操作二，那么一定都是删最左边一列和最下面一行的。所以如果 \(X\) 和 \(Y\) 确定了，那么最多能删多少个也就确定了。

发现阶梯的块数一定是 \(\sqrt n\) 个（赛时没想到），可以枚举 \(X : 0 \rightarrow \sqrt n\) 的同时，枚举 \(Y : 0 \rightarrow \sqrt n\)。这样就一定存在一个 \(k= X+Y\) 得到最大值，且不会漏解。

这一过程时间复杂度就是 \(O(n)\) 了。

注意枚举的上界要开到 \(\sqrt{2n}\) （阶梯是等腰直角三角形）。

反思：有什么发现的性质就写纸上，可能有用。

点击查看代码

#include <iostream>
#include <algorithm>
#include <math.h>
using namespace std;
const int N=1e6+5;
int n,p,a[N],b[N],cnt[N],sum[N],ans[N],pos[N],res[N];
bool cmp(int x,int y){return cnt[x]>cnt[y];}
void sol(){
	scanf("%d",&n);
	p=0;
	for(int i=1;i<=n;++i) cnt[i]=0;
	for(int i=1;i<=n;++i){
		scanf("%d",&a[i]);
		if(!cnt[a[i]]) b[++p]=a[i];
		cnt[a[i]]++;
	}
	sort(b+1,b+p+1,cmp);
	int r=sqrt(n)*1.4;
	pos[0]=p;
	for(int i=0;i<=3*r;++i) ans[i]=res[i]=0;
	for(int i=1;i<=r;++i){
		pos[i]=pos[i-1];
		while(pos[i]>=1&&cnt[b[pos[i]]]<=i) --pos[i];
		res[i]=res[i-1]+pos[i-1];
	}
	for(int x=0;x<=r;++x)
		for(int y=0;y<=r;++y) if(x+y>0){
			int tmp=0;
			for(int i=1;i<=x&&i<=pos[y];++i){
				if(cnt[b[i]]<=y) break;
				tmp+=cnt[b[i]]-y;
			}
			tmp+=res[y];
			ans[x+y]=max(ans[x+y],tmp);
		}
	for(int i=2*r;i>0;i--) for(int j=1;j<=ans[i]-ans[i-1];++j)
		printf("%d ",i);
	puts("");
}
int main(){
	int c,T; scanf("%d%d",&c,&T);
	while(T--) sol();
}

---

CSP Round 7

T3

区间 dp。

怎么想到是区间 dp 呢？

1. \(n \le 500\)。
2. 可以划分成子区间，而且子区间之间是独立的。
3. 子区间可以相互推导。

设 \(f_{i,j}\) 表示只考虑区间 \([i,j]\) ，而且考虑保留 \(i-1\) 和 \(j+1\) 的答案。

转移式：

\[f_{i,j} = \sum_{k=i}^j f_{i,k-1} \times f_{k+1,j} \times \binom{j-i}{j-k} \times [a_{i-1}\not = a_k \land a_k \not= a_{j+1}] \]

相当于处理这个区间时，枚举这个区间的最后一个被删去的，然后看左右两边的情况。乘一个组合数是因为左右两边的顺序可以打乱（可以从二进制的角度考虑）。

答案为 \(f_{1,n}\)。

点击查看代码

#include <bits/stdc++.h>
using namespace std;
#define ll long long
int n;
const int N=505;
int a[N],C[N][N],dp[N][N];
ll mod=1e9+7;
int main(){
	scanf("%d",&n);
	C[0][0]=1;
	for(int i=1;i<=n;++i)
		for(int j=C[i][0]=1;j<=i;++j)
			C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;
	for(int i=1;i<=n;++i) scanf("%d",&a[i]),dp[i][i-1]=1;
	dp[n+1][n]=1;
	for(int len=1;len<=n;++len)
		for(int i=1,j=i+len-1;j<=n;++i,++j)
			for(int k=i;k<=j;++k){
				if((i>1&&a[i-1]==a[k])||(j<n&&a[j+1]==a[k])) continue;
				dp[i][j]=((ll)dp[i][j]+1ll*dp[i][k-1]*dp[k+1][j]%mod*C[j-i][j-k])%mod;
			}
	printf("%d\n",dp[1][n]);
}

---

NOIP 20 Round 14

T2

考虑最终情况的题。

用 \(f_{i,j}\) 表示以第 \(i\) 个数开头，0 的数量 \(\le j\) 的最长区间长度。

用 \(g_{i,j}\) 表示以第 \(i\) 个数结尾，0 的数量 \(\le j\) 的最长区间长度。

在处理一个 \(j\) 时，所有的 \(i\) 显然可以双指针。因此 \(f,g\) 都是可以 \(O(n^2)\) 求出来的。

令 \(ans_i\) 表示使用合法数量的变换操作下，最长 0 的连续段长度为 \(i\) 时，1 的连续段的最长长度。

那么枚举 $ l \le r$，令 \(k'=\) 区间 \([l,r]\) 中 1 的数量。

如果 \(k' \le k\)，更新：

\[ans_{r-l+1} \leftarrow \max ( \max_{i=r+1}^{n} f_{i,k-k'}, \max_{i=1}^{l-1} g_{i,k-k'}) \]

那么这个式子处理出 \(f,g\) 的前缀 \(\max\) 即可。可以 \(O(1)\) 更新。枚举是 \(O(n^2)\) 的。

那么对于 \(i= 1 , 2 ,\cdots\) 的答案，为 \(\max \{ i \times j + ans_j\}\)。

点击查看代码

#include <bits/stdc++.h>
using namespace std;
int n,k;
const int N=3005;
char str[N];
int sum[N],ans[N],f[N][N],F[N][N],g[N][N],G[N][N];
void sol(){
	scanf("%d%d",&n,&k);
	scanf("%s",str+1);
	F[0][n+1]=G[0][0]=0; ans[0]=-1;
	for(int i=1;i<=n;++i){
		ans[i]=-1;
		F[i][n+1]=0; G[i][0]=0;
		sum[i]=sum[i-1]+str[i]-'0';
	}
	for(int i=0;i<=n;++i){
		int r=0;
		for(int l=1;l<=n;++l){
			while(r<n&&(r+1-l+1)-(sum[r+1]-sum[l-1])<=i) ++r;
			f[i][l]=r-l+1;
		}
	}
	for(int i=0;i<=n;++i)
		for(int j=n;j>=1;j--)
			F[i][j]=max(F[i][j+1],f[i][j]);
	for(int i=0;i<=n;++i){
		int l=1;
		for(int r=1;r<=n;++r){
			while((r-l+1)-(sum[r]-sum[l-1])>i) ++l;
			g[i][r]=r-l+1;
		}
	}
	for(int i=0;i<=n;++i)
		for(int j=1;j<=n;++j)
			G[i][j]=max(G[i][j-1],g[i][j]);
	for(int i=1;i<=n;++i)
		for(int j=i;j<=n;++j){
			int s=sum[j]-sum[i-1];
			if(s>k) continue;
			int len=max(F[k-s][j+1],G[k-s][i-1]);
			ans[j-i+1]=max(ans[j-i+1],len);
		}
	for(int i=1;i<=n;++i){
		int tmp=0;
		for(int j=0;j<=n;++j) if(~ans[j]) tmp=max(j*i+ans[j],tmp);
		printf("%d ",tmp);
	}
	printf("\n");
}
int main(){
	int c,T; scanf("%d%d",&T,&c);
	while(T--) sol();
}

---

T3

结论：如果把这些数可以划分成两个集合，两个集合的和相等就后手胜，否则先手胜利。

证明：

如果可以划分，那么先手选一个集合中的数，后手选另一个集合，那么这两个集合的数还是相等的，因为减的值相同。

如果不可以划分，那么后面一定不可以划分。反证：如果存在 \(a \ge b\)，操作后满足 \(sum_1 + (a-b) = sum_2\)，在操作前就可以 \(sum_1 + a = sum_2 + b\)。

这就成一个背包了，可以一次询问 \(O(nV^2)\) 解决。可以用 bitset 优化，一次询问的复杂度就变成了 \(O(\frac{nV^2}{w})\)。

点击查看代码

#include <bits/stdc++.h>
using namespace std;
const int N=303;
int a[N],sum[N],n,q;
bitset<N*N> tmp;
void sol(){
	scanf("%d%d",&n,&q);
	for(int i=1;i<=n;++i) scanf("%d",&a[i]),sum[i]=sum[i-1]+a[i];
	while(q--){
		int l,r; scanf("%d%d",&l,&r);
		int g=sum[r]-sum[l-1];
		if(g&1){puts("Sensei");continue;}
		tmp.reset();
		tmp[0]=1;
		for(int i=l;i<=r;++i) tmp|=(tmp<<a[i]);
		puts(tmp[g/2]?"Kotoba":"Sensei");
	}
}
int main(){
	int T,id; scanf("%d%d",&T,&id);
	while(T--) sol();
}

---

NOIP 20 Round 16

T2

没有进行充分认真的思考。

结论：最终答案只有两种情况，第一种是区间长恰好为 \(k\)，第二种是区间的左右端点的数相同。

对于第一种，只需要维护长度为 \(k\) 的双指针求区间众数即可。

对于第二种，二分最终答案（0.0 到 1.0 之间）。

假设 \(m\) 是要求的众数，那么假设不等于 \(m\) 的为 \(mid\)，等于 \(m\) 的为 \(1.0-mid\)。那么就是找一个长度大于等于 \(k\) 的区间，满足区间和 \(\ge 0\)。这一过程可以维护前缀 min 来实现。

点击查看代码

#include <bits/stdc++.h>
using namespace std;
const int N=1e6+5;
double eqs=1e-10;
int n,k;
int a[N],d[N],cnt[N];
vector<int> vec[N];
int tmp=0,num=0;
void add(int x){
	++d[a[x]];
	cnt[d[a[x]]-1]--;
	cnt[d[a[x]]]++;
	if(tmp==d[a[x]]) ++num;
	else if(tmp<d[a[x]]) tmp=d[a[x]],num=1;
}
void del(int x){
	d[a[x]]--;
	cnt[d[a[x]]]++;
	cnt[d[a[x]]+1]--;
	if(tmp==d[a[x]]+1){
		--num;
		if(!num) tmp--,num=cnt[d[a[x]]];
	}
}
int check(double t){
	double w0=-t,w1=1.0-t;
	for(int w=1;w<=n;++w){
		if(vec[w].empty()) continue;
		int m=vec[w].size(),r=0,l=-1;
		double mn=1e7;
		for(int i:vec[w]){
			while(l<m && i-vec[w][l+1]+1>=k){
				++l;
				double f=w0*(double)(vec[w][l]-1)+(double)l;
				if(mn-f>eqs) mn=f;
			}
			++r;
			double now=w0*(double)i+(double)r;
			if(l>=0&&now-mn>eqs) return 1;
		}
	}
	return 0;
}
int main(){
	scanf("%d%d",&n,&k);
	for(int i=1;i<=n;++i){
		scanf("%d",&a[i]);
		vec[a[i]].push_back(i);
	}
	for(int i=1;i<=k;++i) add(i);
	int mx=tmp;
	for(int i=1,j=k+1;j<=n;++i,++j){
		add(j); del(i);
		mx=max(mx,tmp);
	}
	double ans=(double)mx/(double)k;
	double l=ans,r=1.0;
	while(r-l>eqs){
		double mid=(l+r)/2.0;
		if(check(mid)) ans=l,l=mid;
		else r=mid;
	}
	printf("%.9lf\n",ans);
}

---

NOIP 20 Round 18

T2

为什么想到区间 dp 了，想到左端点右偏和右端点左偏但还是不会呢？

设 \(f(l,r)\) 表示合并 \([l,r]\) 内的点的最小代价。注意到这样设是根本没办法转移的。所以改成 \(f(l,r)\) 表示把 \([l,r]\) 内的点合并成一条线的最小代价（如果可以）。

虽然这样还是没法转移，但是可以发现最后合并一定长这样。

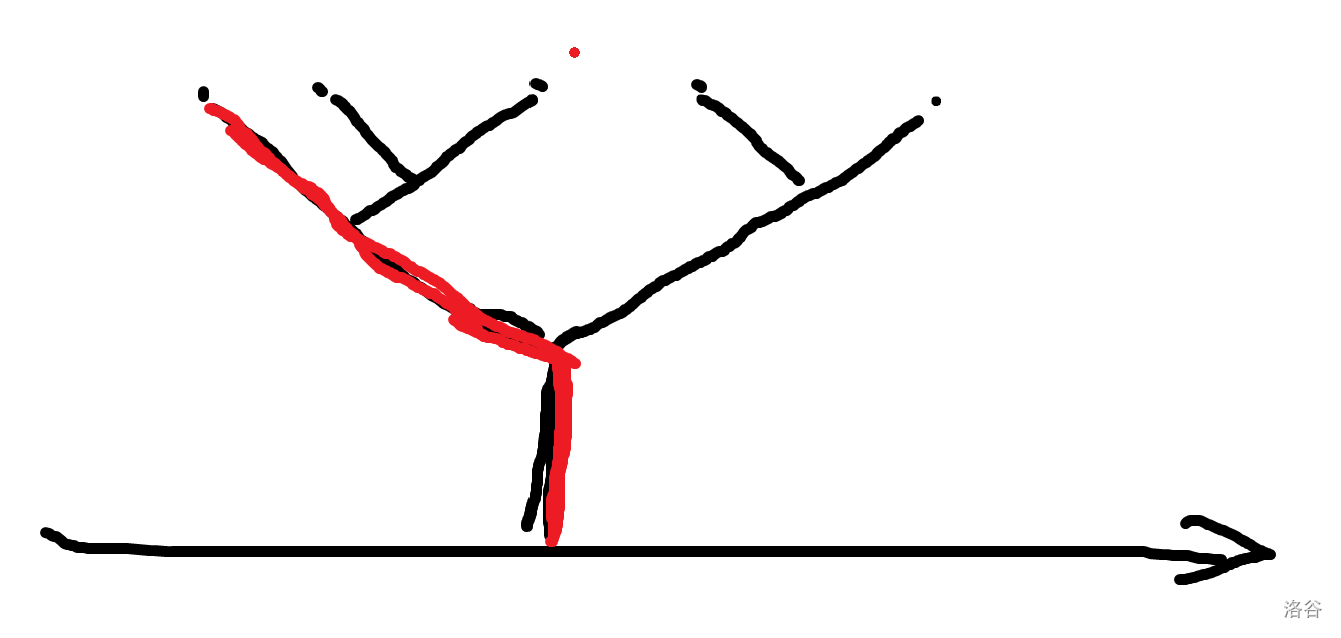
红色部分必定存在而且固定为 \(h\)。所以，\(f(l,r)\) 表示把 \([l,r]\) 内的点合并成一条线的最小代价 \(-h\)（如果可以）。

状态转移：\(f(l,r) \leftarrow f(l,k) + f(k+1,r) + \lfloor \frac{x_r - x_l - 1}{2} \rfloor\)。

但是最终情况不一定只有条线，所以要把 \(1,2,\dots n\) 分成若干合法段。

令 \(g(r,k)\) 表示以点 \(r\) 结尾，当前分成了 \(k\) 段的答案。

状态转移：\(g(r,k) \leftarrow g(l,k-1)+f(l+1,r)\)。

最后答案就是最小的 \(g(n,k) + h \times k\)。

一个正确的考场思路应该是这样的：

• 发现可以合并，\(n \le 500\)，考虑区间 dp。
• 如果直接设区间 \([l,r]\) 最小代价是不是不好合并，等等，最终情况一定是若干直线触底。如果区间 \([l,r]\) 合并成一条直线的最小代价，那么就可以分层若干段，这个是比较好 \(n^3\) dp 的。
• 但是区间 \([l,r]\) 合并成一条直线的最小代价还是不好合并。等等，每一个这个一定存在 \(h\)。所以就可以 \(-h\) 地转移，最后再加一下，差不多做完了

点击查看代码

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N=505;
int c[N][N],a[N],n,h;
ll f[N][N],g[N][N];
int main(){
	scanf("%d%d",&n,&h);
	for(int i=1;i<=n;++i) scanf("%d",&a[i]);
	for(int i=1;i<=n;++i)
		for(int j=i;j<=n;++j){
			c[i][j]=(a[j]-a[i]-1)>>1;
			f[i][j]=(i==j?0:1e17);
		}
	for(int len=2;len<=n;++len)
		for(int i=1,j=i+len-1;j<=n;++i,++j)
			if(c[i][j]<=h) for(int k=i;k<j;++k)
				f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]+c[i][j]);
	for(int i=0;i<=n;++i)
		for(int j=0;j<=n;++j) g[i][j]=1e17;
	g[0][0]=0;
	for(int i=1;i<=n;++i)
		for(int j=0;j<i;++j)
			for(int k=0;k<=j;++k)
				g[i][k+1]=min(g[i][k+1],g[j][k]+f[j+1][i]);
	ll ans=1e18;
	for(int i=1;i<=n;++i) ans=min(ans,g[n][i]+1ll*h*i);
	printf("%lld\n",ans);
}

---

NOIP 20 Round 19

T2

显然一个串最多会有两条出边。

这个图显然是一棵树，答案就是节点的数量。

如果 \(s\) 的每个相邻字符两两不同，那么就有两条出边。此时答案为 \(\sum_{i=0}^{n-1} 2^i = 2^n-1\)。

接下来考虑去重，如果一个极大子串 \([l,r]\) 内的每一个字符都相同，那么这个点以下的所有子孙节点的出边只有一条。令 \(k=r-l+1\)，那么对答案就会减去 \(2^k-1 -k\)。而且这样的串不止出现一次，所以这样的贡献还需要乘上 \(\binom{n-k}{l-1}\)，表示一共需要删 \(n-k\) 次，其中要删 \(l-1\) 次左端点。

但是还有问题，这个极大子串的前缀串或者后缀串也会出现在树中：

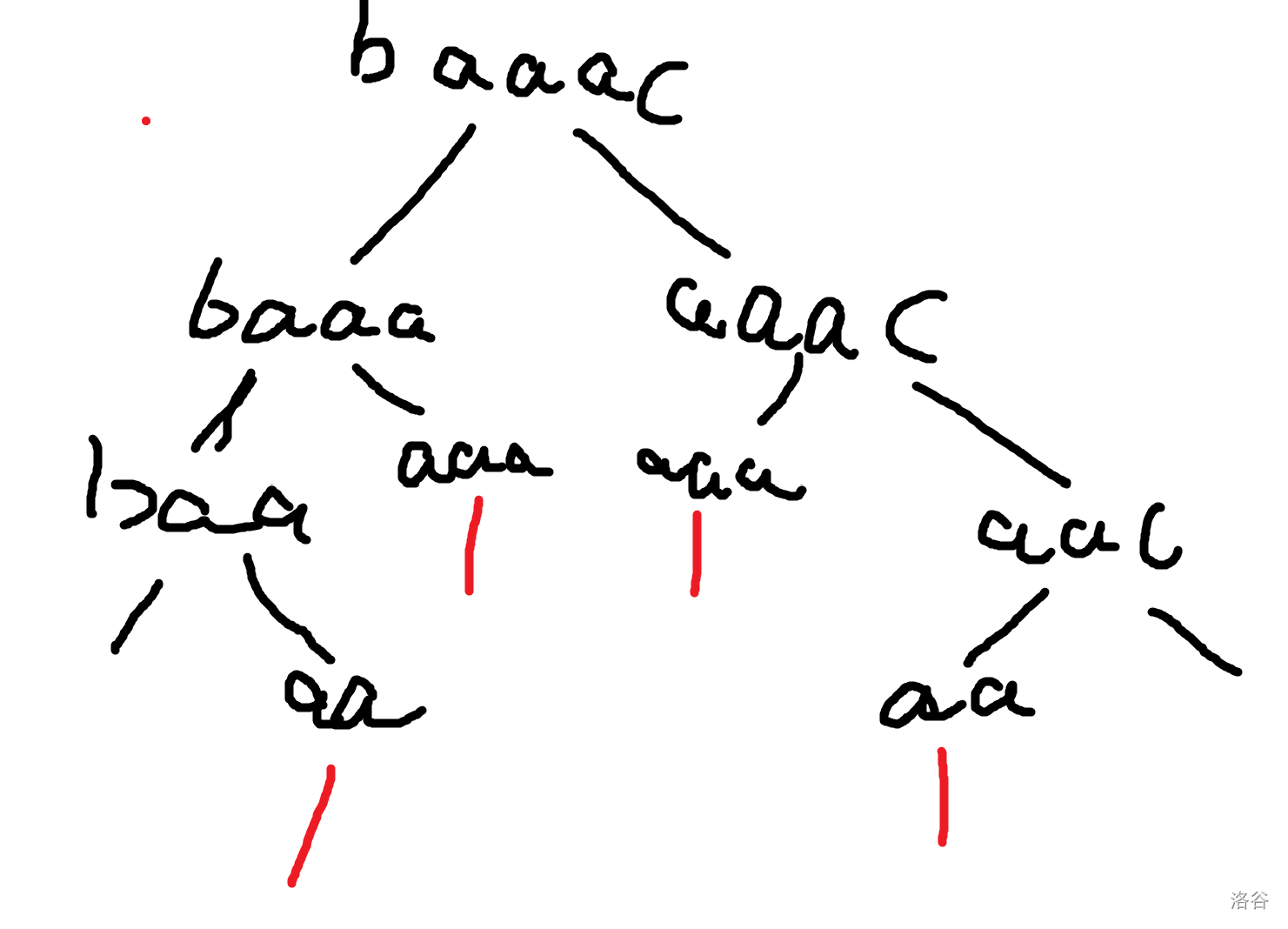
那么还需要求每一个前缀串的贡献。假设某一个前缀串是 \([l,r]\)，要想不被误经过极大串，最后一个操作一定是删左端点。因此需要乘 \(\binom{n-k-1}{l-2}\)，右端点同理。

点击查看代码

#include <bits/stdc++.h>
using namespace std;
int n;
const int N=2e5+5;
char str[N];
int f[N],g[N];
#define ll long long
ll mod=998244353;
int inv(int x){
	int r=1,b=mod-2;
	while(b){
		if(b&1) r=1ll*r*x%mod;
		b>>=1;  x=1ll*x*x%mod;
	}
	return r;
}
int C(int n,int m){
	return 1ll*g[n]*inv(g[m])%mod*inv(g[n-m])%mod;
}
int solve(int l,int r){
	return C(n-(r-l+1),l-1);
}
int main(){
	scanf("%d",&n);
	scanf("%s",str+1);
	f[0]=g[0]=1;
	for(int i=1;i<=n;++i) f[i]=1ll*f[i-1]*2%mod,g[i]=1ll*g[i-1]*i%mod;
	int l=1,r=1,ans=f[n]-1;
	str[n+1]='A';
	for(;r<=n+1;++r){
		if(str[l]!=str[r]){
			--r;
			if(r-l+1>1){
				ans=(ans-1ll*solve(l,r)*(f[r-l+1]-1-(r-l+1))%mod+mod)%mod;
				if(1<l) for(int i=l+1;i<r;++i) ans=(ans-1ll*solve(l-1,i)*(f[i-l+1]-1-(i-l+1))%mod+mod)%mod;
				if(r<n) for(int i=r-1;i>l;i--) ans=(ans-1ll*solve(i,r+1)*(f[r-i+1]-1-(r-i+1))%mod+mod)%mod;
			}
			l=r+1;
		}
	}
	printf("%d\n",ans);
}

---

NOIP 20 Round 20

T2

死因：没有正确挖掘图的性质和分析数学式子。

\(y|x+n\) 相当于 \(by=x+n,-n \equiv x \pmod y\)，因为 \(x<y\)，所以 \(x = y-n \bmod y\)。故这样的 \(x\) 是唯一的。

也就是说，一个点至多会和一个小于它的点连边（如果 \(y|n\) 就没有）。所以原图是一个森林，不妨设比它小的是它的父亲。发现这个深度一定不超过 \(O(\sqrt n)\)，直接暴力跳就行了。

点击查看代码

#include <bits/stdc++.h>
using namespace std;
int n,u,v;
#define _i __int128
map<int,_i> mp;
void w(_i res){
	int stk[100],top=0;
	do{
		stk[++top]=res%(_i)10;
		res/=(_i)10;
	}while(res>0);
	while(top) printf("%d",stk[top--]);
	printf("\n");
}
void sol(){
	mp.clear();
	scanf("%d%d%d",&n,&u,&v);
	int now=u;
	mp[now]=0;
	while(n%now){
		int ne=((now-n)%now+now)%now;
		mp[ne]=mp[now]+(_i)now*(_i)ne;
		now=ne;
	}
	now=v; _i ans=0;
	while(1){
		if(now==u||mp[now]){
			w(mp[now]+ans);
			return ;
		}
		if(n%now==0) break;
		int ne=((now-n)%now+now)%now;
		ans+=(_i)ne*(_i)now;
		now=ne;
	}
	puts("-1");
}
int main(){
	int T; scanf("%d",&T);
	while(T--) sol();
}

---

T3

结论，一定存在一种最优解，满足是若干段通过交换匹配，每段之间是由一个取反操作隔开。

这个很好证明，因为如果交换操作和取反操作路径有交叉一定不优。

记第 \(i\) 个位置为结尾，最大的 \(j < i\)，满足 \([j,i]\) 中 \(\sum b_t = \sum a_t\) 的位置，记为 \(pre_i\)。

可以发现，如果要让这个区间的每个位置通过交换进行匹配，移动的位置必定都是同方向的。因为出现不同方向时，中间可以划开成更小的区间。

那么我们可以记录一个 \(g(x)\)，表示 \(g(x) = \sum_{i=1}^x (a_i - b_i) \times i\)。那么对于一个 \([pre_i,i]\) 区间，匹配的交换次数就是 \(|g(i)-g(pre_i-1)|\)。

可以 dp 解决，设 \(f(i)\) 表示前 \(i\) 个完成匹配的方案，状态转移：

• \(f(i) \leftarrow f(i-1) + Y[a_i \not= b_i]\)
• \(f(i) \leftarrow f(pre_i-1) + X|g(i)-g(pre_i-1)|\)

像这种记录最小区间（记录上一个需要的位置）的方法在 CSP-S 2024 T3染色 中也会遇到。

点击查看代码

#include <bits/stdc++.h>
using namespace std;
int n,x,y;
const int N=1e7+5;
char a[N],b[N];
#define ll long long
int las[N<<1],sum[N];
ll g[N],f[N];
void sol(){
	scanf("%d%d%d%s%s",&n,&x,&y,a+1,b+1);
	for(int i=0;i<=2*n;++i) las[i]=-1;
	las[n]=f[0]=g[0]=0; sum[0]=n;
	for(int i=1;i<=n;++i){
		sum[i]=sum[i-1]-(a[i]-b[i]);
		g[i]=g[i-1]+(a[i]-b[i])*i;
		f[i]=f[i-1]+(a[i]!=b[i])*y;
		if(~las[sum[i]]){
			f[i]=min(f[i],f[las[sum[i]]]+1ll*abs(g[i]-g[las[sum[i]]])*x);
		}
		las[sum[i]]=i;
	}
	printf("%lld\n",f[n]);
}
int main(){
	int T; scanf("%d",&T);
	while(T--) sol();
}

---

洛谷 SCP-NOIP 模拟赛

T3

容易发现如果只考虑子树的答案，那么这个答案的贡献向上合并时每一个 \(f(v+d)\) 都会变成 \(f(v+d-1)\)，又因为 \(f(x)\) 和二进制有关系，就可以用 01-Trie 合并来实现。

对于子树外的答案也可以利用这个合并求得。

题解+code。

---

NOIP Round 10

T1

赛时糖丸了。

显然 A 最后操作两个数一定赢，B 操作后两个数如果不全是 0 就是 B 赢，否则 A 赢。

所以只考虑 B 操作后两个数。显然 B 是要让 1 尽可能多，A 要让 0 尽可能多。又因为连续的 1 可以抵消掉，所以只需要看 1 和 0 的数量即可。

点击查看代码

#include <bits/stdc++.h>
using namespace std;
int n,m,sum=0;
const int N=1e5+5;
int a[N];
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;++i) scanf("%d",&a[i]),sum+=(a[i]&1);
	int gum=n-sum;
	if(n==1) return !puts(sum?"B":"A");
	if(!((n+m)&1)) return !puts("A");
	int las=0,odd=0,even=0;
	for(int i=1;i<=n;++i){
		odd+=a[i]&1;
		even+=a[i]+1&1;
		if(las&a[i]&1){
			odd-=2;
			las=0;
		}
		else las=a[i]&1;
	}
	puts(odd>=even?"B":"A");
}

---

T2

赛时思路：

考虑建图，令 $ \forall j \in [l_i , r_i]$，建有向边 \(j \rightarrow i\)，如果将一个点染黑，这个点能到达的所有点也会被染黑，代价就是会舍弃这个点的价值 \(v_x\)。

考虑缩点，对每一个入度为 0 的 SCC 找其中 \(v\) 最小的一个舍弃即可，时间复杂度 \(O(n^2)\)。

因为不知道线段树优化建图所以扔了 20 分。。

上面的建图方式使得在找点 \(x\) 指向的点 \(y\) 需要满足 \(l_y \le x \le r_y\)，这个不太好找，所以考虑将所有边取反，这样对 SCC 是没有影响的，而且找点 \(x\) 指向的点 \(y\) 需要满足 \(l_x \le y \le r_x\)，最后就是从找入度为 0 变成出度为 0 就行了。

我们考虑在跑 Tarjan 时维护两棵线段树，一棵记录这个点的 \(dfn\) 是否为 0，一棵记录目前在栈中的点的 \(dfn\) 值的最小值（其实可以变成一棵线段树）。如果这个点能沿树边走到一个点就记录这条边，既可以在缩点时及时处理出度，也不会爆时空（树边最多只有 \(n-1\) 条）。

点击查看代码

#include <bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int n,inf=1e9,cd[N],l[N],r[N],v[N];
int dfn[N],low[N],tot=0;
int stk[N],in[N],top=0;
int scc[N],tmp[N],cnt=0;
#define mid ((l+r)>>1)
#define lc (u<<1)
#define rc (u<<1|1)
struct TREE{
	int t[N*4];
	void build(int u,int l,int r){
		t[u]=r-l+1;
		if(l==r) return ;
		build(lc,l,mid); build(rc,mid+1,r);
	}
	int query(int u,int l,int r,int x,int y){
		if(t[u]<=0) return -1;
		if(l==r) return l;
		int ans=-1;
		if(x<=mid&&t[lc]){
			ans=query(lc,l,mid,x,y);
			if(~ans) return ans;
		}
		if(y>mid&&t[rc]){
			ans=query(rc,mid+1,r,x,y);
			if(~ans) return ans;
		}
		return -1;
	}
	void del(int u,int l,int r,int x){
		t[u]--;
		if(l==r) return ;
		if(x<=mid) del(lc,l,mid,x);
		else del(rc,mid+1,r,x);
	}
}T;
struct TRer{
	int t[N*4];
	void pushup(int u){t[u]=min(t[lc],t[rc]);}
	void build(int u,int l,int r){
		t[u]=inf;
		if(l==r) return ;
		build(lc,l,mid); build(rc,mid+1,r);
	}
	int query(int u,int l,int r,int x,int y){
		if(t[u]==inf) return inf;
		if(x<=l && r<=y) return t[u];
		int ans=inf;
		if(x<=mid) ans=min(ans,query(lc,l,mid,x,y));
		if(y>mid) ans=min(ans,query(rc,mid+1,r,x,y));
		return ans;
	}
	void upd(int u,int l,int r,int x,int k){
		if(l==r) return void(t[u]=k);
		if(x<=mid) upd(lc,l,mid,x,k);
		else upd(rc,mid+1,r,x,k);
		pushup(u);
	}
}R;

vector<int> e[N];
void Tarjan(int u){
	T.del(1,1,n,u);
	low[u]=dfn[u]=++tot;
	R.upd(1,1,n,u,tot);
	stk[++top]=u;
	in[u]=1;
	low[u]=R.query(1,1,n,l[u],r[u]);
	vector<int> vec;
	while(1){
		int v=T.query(1,1,n,l[u],r[u]);
		if(v==-1) break;
		if(!dfn[v]){
			e[u].push_back(v);
			Tarjan(v);
			low[u]=min(low[u],low[v]);
		}
	}
	if(dfn[u]==low[u]){
		++cnt; tmp[cnt]=1e9;
		int y;
		do{
			y=stk[top--];
			in[y]=0;
			scc[y]=cnt;
			tmp[cnt]=min(tmp[cnt],v[y]);
			R.upd(1,1,n,y,inf);
		}while(u^y);
	}
}
#define ll long long
int main(){
	scanf("%d",&n);
	ll ans=0;
	for(int i=1;i<=n;++i) scanf("%d%d%d",&l[i],&r[i],&v[i]),ans+=v[i];
	T.build(1,1,n);
	R.build(1,1,n);                
	for(int i=1;i<=n;++i) if(!dfn[i]) Tarjan(i);
	for(int x=1;x<=n;++x)
		for(int y:e[x]) if(scc[x]^scc[y]){
			cd[scc[x]]++;
		}
	for(int i=1;i<=cnt;++i) if(!cd[i]) ans-=tmp[i];
	printf("%lld\n",ans);
}

---

杂题乱刷

P3520 [POI 2011] SMI-Garbage

给定一张无向图，只能走简单环，要求一些边恰好走奇数次，剩下的边走恰好偶数次，可以走很多个简单环，输出一种合法方案或报告无解。

核心思想：把需要走偶数次的边变成两条重边，奇数次的边不动，这样问题就变成了每条边恰好走一次的方案。

使每条边恰好走一次与欧拉图的特点一样，只需要找出欧拉回路，在 dfs 时及时弹栈找到所有简单环即可。

ABC261E

给你 \(N\) 次基本操作和初始值 \(X\)，每次基本操作都是按位与、或、异或三种，对于第 \(i\) 次操作，将 \(X\) 从第 \(1\) 个基本操作依次执行到第 \(i\) 个基本操作并输出现在的 \(X\)。

模拟赛半小时就把这题切掉了，还是很开心的。

核心思想：位运算时，二进制下的每一位之间互不影响。

考虑拆位，提前处理出每一位依次执行操作后的数的情况，更新 \(X\) 时，只需要找这一位在运算后对应的数，有点类似于维护一个很小映射。

CF1245D

完全图，\(N\) 个点（\(N\le 2000\)），点有点权，边有边权，每个点初始为白色。可以一个点花费这个点的点权让这个点变成黑色，可以花费这个边的边权建这条边。求使得所有点都能通过建好的边走到黑点的最小花费。

点权转化成边权，建立一个超级源点，让其他每个点向这个点连边，边权就是点权，然后跑 Prim 求最小生成树即可。

P8862 「KDOI-03」还原数据

每一个 \(\max\) 操作对答案的加的贡献显然被后面的 \(\max\) 操作抵消掉，因为是 \(\max\) 操作后不存在一个数变得更小，所以考虑倒序处理答案。

每个加操作变成减操作，发现每一个 \(\max\) 操作中的数 \(x\) 显然要小于等于 \(\min_{i=l}^{r} a_i\)，要不然就不合法。贪心让每一个 \(x\) 都取等就是正确答案。

线段树维护区间加、区间求 \(\min\)，而且初始数组对答案是没有影响的。

P14221 [ICPC 2024 Kunming I] 学而时习之

trick：对于每一个前缀 \(\gcd\)，其取值最多只有 \(\log V\) 种，其中 \(V\) 是值域。

答案一定是这种形式：\(\gcd(pre_{l-1} , a_l + k , a_{l+1}+k, \dots , a_r+k,bac_{r+1})\)。

如果存在一个 \(i\) 满足 \(pre_i = pre_{i-1}\)，那么 \(l\) 取 \(i+1\) 一定不比 \(l\) 取 \(i\) 劣。因为前缀 \(\gcd\) 不变，中间的部分多了一个数，这可能会导致最终答案更小。

\(bac\) 的情况也同理。

CF2154C2

\(n\) 个正整数 \(a_i\)，可以花费 \(b_i\) 的代价使得 \(a_i\) 加一。求存在 $ i \not = j$ 且 \(\gcd(a_i,a_j)>1\) 的最小花费。

只有两种情况：

1. 两个数同时加一次一。
2. 一个数加很多次一。

第 1 种情况很简单，重点是第 2 种。

结论：被加的这个数一定是 \(b_i\) 的那一个。

反证：假设最小的是 \(b_1\)。如果 \(b_x \ge b_1\)，那么需要花费就是 \(b_x \times k \: (k \ge 2)\)，那么一定有 \(b_1 + b_x \le b_x \times k\)。所以与其操作 \(k\) 次 \(x\)，还不如操作一次 \(1\) 一次 \(x\)。

P9118 [春季测试 2023] 幂次

\([1,n]\) 中能被表示成 \(a^b,b\ge k\) 的数有多少个。\(n \le 10^{18}\)。

trick：\([1,n]\) 中的完全平方数共有 \(\sqrt n\) 个。

可以先处理 \(k \ge 3\) 的情况，再统计有哪些完全平方数被记录答案，最后减一下就行。

P4180 [BJWC2010] 严格次小生成树

首先次小生成树一定是由最小生成树替换一条边得到。

相当于每次在次小生成树上加边，得到一个环。如果加的这个边的大小等于树边的最大值，就减去树边上的严格次大，否则减去树边上的最大。

原问题等价于路径上求最大和严格次大边权，树剖+线段树即可。

像这种每次尝试在树上加边的操作就可以考虑树剖维护信息。（P14080 [GESP202509 八级] 最小生成树）

P5847 [IOI 2005] mea

长度为 \(n\) 的一个不降序列 \(M\)，求有多少个长度为 \(n+1\) 的不降序列 \(S\)，满足 \(S_i + S_{i+1}= 2M_i\)

不等式分离技巧。

容易发现 \(S_1\) 确定了，那么整个 \(S\) 就确定了。

尝试把所有的 \(S\) 写成 \(S_1\) 的形式。

\[\begin{aligned} S_1 &= S_1 \\ S_2 &= 2M_1 - S_1 \\ S_3 &= 2M_2 - 2M_1 + S_1 \\ S_4 &= 2M_3 - 2M_2 + 2M_1 - S_1 \\ \end{aligned} \]

因为 \(S_i \le S_{i+1}\)。

若 \(S_{i+1}\) 中，\(i\) 是偶数：

\[\begin{aligned} 2(M_{i-1} - M_{i-2} + M_{i-3} - \dots + M_1) - S_1 &\le 2(M_{i} - M_{i-1} + M_{i-2} - \dots - M_1) + S_1 \\ -M_i + 2M_{i-1} - 2M_{i+2} + \dots + 2M_1 & \le S_1 \end{aligned} \]

若 \(i\) 是奇数：

\[\begin{aligned} 2(M_{i-1} - M_{i-2} + M_{i-3} - \dots - M_1) + S_1 &\le 2(M_{i} - M_{i-1} + M_{i-2} - \dots + M_1) - S_1 \\ M_i - 2M_{i-1} + 2M_{i+2} - \dots + 2M_1 & \ge S_1 \end{aligned} \]

前缀和维护区间即可。

分离不等式要尽可能把已知量放在一起。

ABC431F

一个长度为 \(n\) 的序列 \(A\) 和常数 \(D\)，有多少种重排的方式使得任意 \(1\le i < n\) 满足 \(A_i - D \le A_{i+1}\)。

令 \(cnt[x]\) 表示 \(A\) 中 \(x\) 的出现次数。

将 \(A\) 从小到大排序，假设比 \(v\) 小的数已经放好，现在考虑 \(v\) 的情况。

考虑插空法，因为是从小到大考虑，所以不需要考虑前面，只要考虑后面。后面的数必须 \(\ge v -D\)，所以一共会有 \(1 + \sum_{i=v-D}^{v-1} cnt[i]\) 个空可以选择。

问题等价于 \(cnt[v]\) 个相同的球，放入 \(1 + \sum_{i=v-D}^{v-1} cnt[i]\) 个不同的盒子里的方案数。答案为 \(\binom{\sum_{i=v-D}^{v} cnt[i]}{cnt[v]}\)。

因此本题答案就是：

\[\prod \binom{cnt[v-D] + \dots + cnt[v]}{cnt[v]} \]

P10102 [GDKOI2023 提高组] 矩阵

三个长宽均为 \(n \le 3000\) 的矩阵 \(A,B,C\)，问 \(A \times B\) 在模 \(998244353\) 意义下是否等于 \(C\)。

随机化做法。

令 \(D\) 是一个 \(n\) 行 \(1\) 列的随机矩阵。如果 \(A \times B = C\)，那么 \(A \times B \times D = C\times D\)。

又因为矩阵乘法满足结合律，所以时间复杂度 \(O(n^3) \rightarrow O(n^2)\)。

P3214 [HNOI2011] 卡农

容易发现每个片段不可区分的条件是假的，可以认为是可区分的，最后除 \(m!\) 就行了。

要选出 \(m\) 个集合为 \(S=\{ 1, 2, \dots , n\}\) 的子集。

有 3 种限制：

1. 所有集合不为空。
2. 没有相同的一对集合。
3. 每个元素在所有集合中的出现次数为偶数。

设 \(f(i)\) 表示前 \(i\) 个集合的合法方案数。那么考虑求 \(f(i)\)，发现如果前 \(i-1\) 个集合确定了，要满足 3，这个集合也就确定了，为 \(A_{2^n-1}^{i-1}\)。

考虑去除违反 1 的方案，只能是第 \(i\) 个集合为空，那么前 \(i-1\) 个集合就是合法的，减去 \(f(i-1)\) 即可。

考虑去除违反 2 的方案，假设是第 \(j\) 个集合与 \(i\) 相同，那么剩下的 \(i-2\) 个集合就是合法的，这样的 \(j\) 有 \(i-1\) 种，可能重合的集合数有 \(2^n-1-(i-2)\) 种，所以要减去 \(f(i-2) \times (i-1) \times (2^n+1-i)\)。

综上，状态转移为 \(f(i) \leftarrow A_{2^n-1}^{i-1} - f(i-1) - f(i-2)\times(i-1) \times (2^n+1-i)\)。

[P3702 SDOI2017] 序列计数 - 洛谷

考虑容斥，求出任意放和不放质数的方案数，减一下就行。

一个显然的 dp 为：设状态 \(f(i,j)\) 表示前 \(i\) 个数的和模 \(p\) 为 \(j\) 的方案数， 那么转移：\(f(i,j) = \sum f(i-1,t) + cnt_{j-t \bmod p}\)。时间复杂度 \(O(np^2)\)。

考虑优化，发现 \(p\) 很小，\(n\) 很大。假设要求矩阵 \(\begin{vmatrix}f(i,0)\\f(i,1)\\ \cdots \\ f(i,p-1) \end{vmatrix}\) ，那么有如下转移：

\[\begin{vmatrix}f(i,0)\\f(i,1)\\f(i,2) \\ \cdots \\ f(i,p-1) \end{vmatrix} = \begin{vmatrix} cnt_{0} & cnt_{p-1} & cnt_{p-2} & \cdots & cnt_{1} \\ cnt_{1} & cnt_{0} & cnt_{p-1} & \cdots & cnt_{2} \\ cnt_{2} & cnt_{1} & cnt_{0} & \cdots & cnt_{3} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ cnt_{p-1} & cnt_{p-2} & cnt_{p-3} & \cdots & cnt_{0} \end{vmatrix} \times \begin{vmatrix} f(i-1,0)\\f(i-1,1)\\f(i-1,2) \\ \cdots \\ f(i-1,p-1) \end{vmatrix} \]

这样复杂度就能降为 \(O(p^3\log n )\)。

[P11870 威海市赛2024] 找数 - 洛谷

很巧妙的计数题。

因为奇数位一定是奇数，偶数位一定是偶数。所以让序列 \(p_i \leftarrow p_i+i\)，这样每个值都是偶数，而且不同的序列经过这个变换之后得到的新序列也是互不相同的。

这样问题就等价于 \(1 \sim n+m\) 中选出 \(m\) 个偶数，答案为 \(\binom{\lfloor \frac{n+m}{2} \rfloor}{m}\)。