解题报告-洛谷P2481 [SDOI2010] 代码拍卖会
P2481 [SDOI2010] 代码拍卖会
题目描述
随着 iPig 在 P++ 语言上的造诣日益提升,他形成了自己一套完整的代码库。猪王国想参加 POI 的童鞋们都争先恐后问 iPig 索要代码库。iPig 不想把代码库给所有想要的小猪,只想给其中的一部分既关系好又肯出钱的小猪,于是他决定举行了一个超大型拍卖会。
在拍卖会上,所有的 \(N\) 头小猪将会按照和 iPig 的好感度从低到高,从左到右地在 iPig 面前站成一排。每个小猪身上都有 \(9\) 猪币(与人民币汇率不明),从最左边开始,每个小猪依次举起一块牌子,上面写上想付出的买代码库的猪币数量(\(1\) 到 \(9\) 之间的一个整数)。大家都知道,如果自己付的钱比左边的猪少,肯定得不到梦寐以求的代码库,因此从第二只起,每只猪出的钱都大于等于左边猪出的价钱。最终出的钱最多的小猪(们)会得到 iPig 的代码库真传,向着保送 PKU(Pig Kingdom University)的梦想前进。
iPig 对自己想到的这个点子感到十分满意,在去现场的路上,iPig 就在想象拍卖会上会出现的场景,例如一共会出现多少种出价情况之类的问题,但这些问题都太简单了,iPig 早已不感兴趣了,他想要去研究更加困难的问题。iPig 发现如果他从台上往下看,所有小猪举的牌子从左到右将会正好构成一个 \(N\) 位的整数,他现在想要挑战的问题是所有可能构成的整数中能正好被 \(P\) 整除的有多少个。由于答案过大,他只想要知道答案 \(\bmod\ 999911659\) 就行了。
输入格式
有且仅有一行两个数 \(N\ (1 \le N \le 10^{18})\) 和 \(P\ (1 \le P \le 500)\),用一个空格分开。
输出格式
有且仅有一行一个数,表示答案除以 \(999911659\) 的余数。
输入输出样例 #1
输入 #1
2 3
输出 #1
15
说明/提示
样例解释
方案可以是:\(12,15,18,24,27,33,36,39,45,48,57,66,69,78,99\),共 \(15\) 种。
数据规模
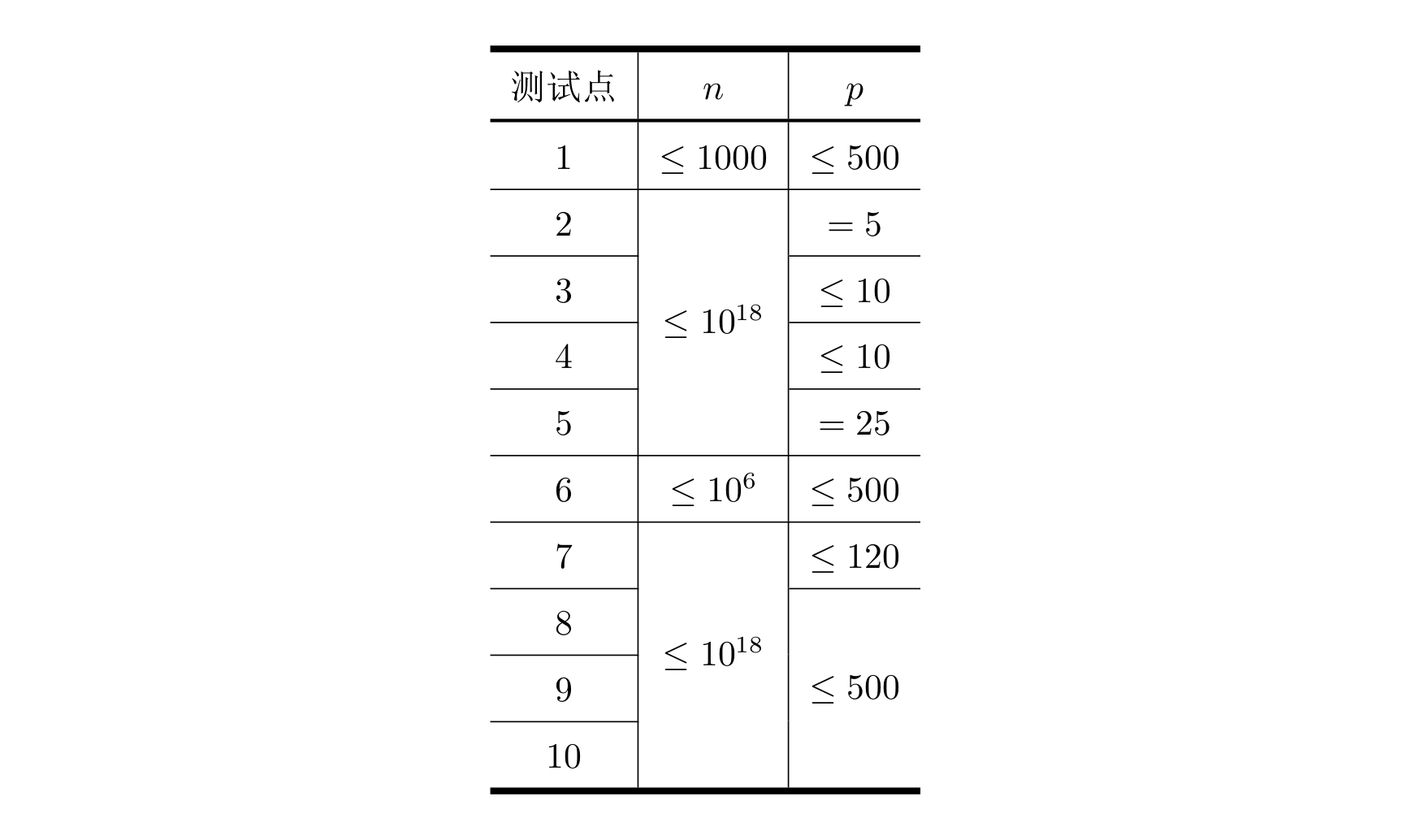
解题报告
最开始的时候觉得:这不明显的数位DP吗?感觉和P4127 [AHOI2009] ]同类分布 - 洛谷差不多,然后一看数据范围: \(10^{18}\)!!!正常的数位DP连数组都开不下!!!
在这个范围内直接解决问题是不现实的,于是开始考虑怎么缩小实际的范围。先从这个题目的性质开始。一个满足题目要求的合法的数字显然是形如 $11111222222223333 \cdots 8899999 $ 的数,这时候,就有一个套路的想法(第一个想到的人太神了,我根本想不到):可以把这个数拆成若干个只由连续的的 \(1\) 组成的数相加。
具体的,例如一个数 \(1111222334\),它可以有如下变换:
那么,我们就可以把任意一个合法的数分割成若干个形如 \(0000 \cdots 111\) 的数相加,为了方便我们称一个形如\(000 \cdots 111\)的数为 \(S_k\),其中,\(k\) 表示有从低位开始的连续的 \(1\) 的个数。例如,我们将数 \(000111111111\) 称为 \(S_9\)。
这样做有一个好处:一个数最多只会由 \(9\) 个这样的数组成。这时,一个暴力的想法出现了:因为只能选 \(9\) 个 \(S_k\),我们就可以跑一个 \(O(n^9)\) 的暴力。当然,这样打一点分的得不到。
但这样给了我们一点思路,观察以下暴力的过程,相当于在进行一个完全背包:总共有 \(n\) 个物品,背包容量为 \(9\),第 \(k\) 物品的价值为 \(S_k\),体积为 \(1\)。可以做一个背包的转移。
但是,\(n\) 实在是太大了,这样做依然不能完全 AC。
我们尝试减少物品数量。实际上,由于同余运算的性质:\((x+y) \mod n = ( ( x \mod n )+(y \mod n) ) \mod n\) ,我们并不关心 \(S_k\) 具体是什么样子,而是关心它在模 \(P\) 下的余数,我们可以预处理出所有可能的 \(S_k\) 在模 \(P\) 情况下的余数,通过这些余数,我们就可以知道一个合法的数是否可以被 \(P\) 整除。
那么,我们将看到,实际上有很多的 \(S_k\) 的余数相同,意味着它们对答案的贡献是相同的。我们可以将相同余数的 \(S_k\) 归为一个同余类,然后通过组合数学求出每一个同余类对答案的贡献。题目中的 \(P\) 不到 \(500\),意味着我们实际的物品数最多也就是 \(500\),相比于之前的 \(10^{18}\),这少了可不止一点。
接下来具体讨论怎么DP:
我们记 某一个\(S_k\) 在模 \(P\) 的意义下的余数为 \(i\),选了多少个 \(S_k\) 记为 \(j\),余数为 \(i\) 的 \(S_k\) 的个数记为 \(g_i\)。
那么可以设状态数组为 \(dp[i][j][s]\) ,表示考虑到余数 \(i\),目前的余数和在模 \(P\) 后的结果为 \(j\)。当前选了 \(s\) 个 \(S_k\)
对于余数 \(i\),我们假设从其同余类中选了 \(t\) 个 \(S_k\),其中 \(s+t \leq 9\)。
那么就有:
其中的 $ \dbinom {g_i+t-1}{t} $ 表示从 \(g_i\) 个不同的 \(S_k\) 中可重复的选 \(t\) 个数的方案数,这是一个经典的结论。
由于 \(t\) 很小,我们直接用公式 \(\dbinom {g_i+t-1}{t}=\dfrac {\amalg_{x=0}^{t-1} (g_i+x)}{t!}\) 计算出所有的 \(\dbinom {g_i+t-1}{t}\),存在数组 \(cc[i][t]\) 中。
还剩下最后一个小问题:怎么计算 \(g_i\)?
对于 \(n \leq P\),我们可以直接暴力求解 \(g_i\)。枚举每一个 \(S_k\),进行统计。
对于 \(n > P\),对于现在的 \(S_k\),设它模 \(P\) 的余数 \(r_k\) 为 \(i\),那么下一个数 \(S_{k+1}=S_{k} \times 10+1\),它模 \(P\) 的余数 \(r_{k+1}\) 为 \((r_{k} \times 10+1) \mod P\),如果一对 \((S_{k1},S_{k2})\),满足 \(r_{k1}==r_{k2}\),那么有 \(r_{k1} \times 10 +1==r_{k2} \times 10 +1\),得 \((r_{k1} \times 10 +1) \equiv (r_{k2} \times 10 +1) \pmod{P}\),最终有 $ S_{k1+1} \equiv S_{k2+1} \pmod{P} $。不断递推下去,可以发现 \(r_k\) 是在不断的循环,
那么就可以求出循环节起始位置和长度,通过数学计算快速求出 \(g_i\)。
还有一些细节,详见代码,算法复杂度为 \(O(9^{2} P^{2})\)。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int INF=0x3f3f3f3f;
const int mod=999911659;
const int N=511;
const int M=10;
inline int read()
{
int f=1,x=0; char ch=getchar();
while(!isdigit(ch)) { if(ch=='-') f=-1; ch=getchar(); }
while(isdigit(ch)) { x=x*10+ch-'0'; ch=getchar(); }
return f*x;
}
int n,P;
int g[N],nR;
int dp[N][N][M];
int cc[N][9];
int pa[N];
inline void calc_g()
{
if(n<=P)
{
int r=0;
for(int i=1;i<=n;i++)
r=(r*10+1)%P,g[r]++;
nR=r;
return ;
}
int r=1%P,len=0,st=0;
for(int i=1;i<=P+1;i++)
{
if(pa[r]) { st=pa[r];len=i-st;break; }
pa[r]=i,g[r]++,r=(r*10+1)%P;
}
for(int i=0;i<P;i++)
if(pa[i] && pa[i]>=st)
{
g[i]+=(n-pa[i])/len%mod;
g[i]%=mod;
if( (pa[i]-st+1)%len==(n-st+1)%len )
nR=i;
}
}
inline int FastPow(int x,int k)
{
int tot=1;x%=mod;
while(k)
{
if(k&1) tot=(tot*x)%mod;
x=(x*x)%mod;
k>>=1;
}
return tot;
}
int fact[N],infact[N];
inline void GetFact()
{
fact[0]=1;
for(int i=1;i<N;i++)
fact[i]=fact[i-1]*i%mod;
infact[N-1]=FastPow(fact[N-1],mod-2);
for(int i=N-2;i>=0;i--)
infact[i]=infact[i+1]*(i+1)%mod;
}
signed main()
{
// freopen("P2481.in","r",stdin);
// freopen("P2481.out","w",stdout);
n=read(),P=read();
calc_g();
GetFact();
for(int i=0;i<P;i++)
{
cc[i][0]=1;
for(int t=1;t<9;t++)
{
cc[i][t]=1;
for(int j=0;j<t;j++)
cc[i][t]=cc[i][t]*( (g[i]+j)%mod )%mod;
cc[i][t]=cc[i][t]*infact[t]%mod;
}
}
dp[0][nR][0]=1;
for(int i=0;i<P;i++)
for(int j=0;j<P;j++)
for(int k=0;k<9;k++)
for(int t=0;t<9-k;t++)
dp[i+1][(j+t*i)%P][k+t]=(dp[i+1][(j+t*i)%P][k+t]+dp[i][j][k]*cc[i][t]%mod)%mod;
int ans=0;
for(int i=0;i<9;i++)
ans=(ans+dp[P][0][i])%mod;
printf("%lld",ans);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号