微积分小感——0.极限论
微积分小感——0.极限论
所需的前置知识:
1)函数的概念
2)实数理论
§1.序列及其极限
—1.序列
想必你小学时做过不少找序列规律的题目,比如下面这些:
对于 \(x_n\) ,相信你能十分轻易的写出通项公式;但对于更复杂的 \(y_n\) ,它的通项公式就很难以初等方法写出;更变态的是 \(z_n\) ,它的第 \(n\) 项就是 \(\pi\) 的前 \(n\) 位小数,通项公式不存在( \(\pi\) 是无理数)。那么到底什么是序列呢?是不是所有序列都要求有一个通项公式呢?且看序列的定义:
对于正整数:
\[1,2,3,\dotsi,n,\dotsi,n',\dotsi \qquad \qquad (1) \]存在对应的实数:
\[x_1,x_2,x_3,\dotsi,x_n,\dotsi,x_{n'},\dotsi \qquad \qquad (2) \]满足当 \(n'>n\) 时 \(x_{n'}\) 在 \(x_n\) 后面,就称 \((2)\) 为序列 \(x_n\) 。
这里的“序列”其实是一种正整数与实数的对应关系,也可以说是一种实数的位次,并不要求有通项公式或者确定的规律。
—2.其极限
对于像序列 \(x_n\) :
我们会发现,随 \(n\) 的增大,\(x_n-0\) 会越来越小,比任意的正数都要小,但又大于 \(0\) 。一个任意的正数都要小但又大于 \(0\) 的数,难道就是无穷小吗?通过简单的反证法[1],我们证明不存在可以称为“无穷小”的实数(即这个差不是所谓“无穷小”),那么怎么用严格的数学语言去描述这个现象呢?这就引出序列的极限的定义:
对于任意正数 \(\epsilon\) ,存在一个正整数 \(N\) ,使在 \(n>N\) 时,一切 \(x_n\) 的值满足
\[\lvert x_n-a \rvert < \epsilon \quad 或 \quad a-\epsilon < x_n < a+\epsilon \quad \qquad (3) \]则常数 \(a\) 称为序列 \(x=x_n\) 的极限,也称变量 \(x\) 趋于 \(a\),记作
\[\lim{x_n}=a \quad 或 \quad x_n \to a \]
这就巧妙的利用了实数的完备性,绕过了拦路的“已死量的幽灵[2]”。这样一个十分巧妙的定义格式被称为“ \(\epsilon-N\) 语言”。
如果把序列 \(x_n\) 的一切取值对应的点表示在数轴上,那么常数 \(a\) 对应的点就是这些点的凝聚中心:
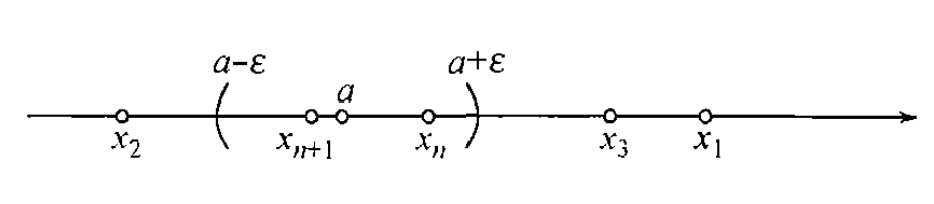
特别的,把序列的极限的定义中的 \((3)\) 换成以下的式子:
\((4)\quad \lvert x_n \rvert < \epsilon\) ,即 \(\lim{x_n}=0\) ,就称 \(x_n\) 为无穷小
\((5)\quad x_n > \Epsilon\) ,就称 \(x_n\) 为正无穷,记作 \(\lim{x_n}=+\infin\) 或 \(x_n \to +\infin\)
("+"常省略)
\((6)\quad x_n < -\Epsilon\) ,就称 \(x_n\) 为负无穷,记作 \(\lim{x_n}=-\infin\) 或 \(x_n \to -\infin\)
§2.极限的定理
—1.定理
由极限的定义,能十分轻易地推得下面的定理:
对于序列 \(x_n\) ,\(y_n\) ,\(z_n\) :
\((Ⅰ)\quad\) 若总有 \(x_n=y_n\) ,则 \(\lim{x_n}=\lim{y_n}\)
\((Ⅱ)\quad\) 若总有 \(x_n>y_n \ (或 \geqslant)\) ,则 \(\lim{x_n} \geqslant \lim{y_n}\) (反之亦然)
\((Ⅲ)\quad\) 夹逼定理[3]:若总有 \(x_n > y_n > z_n \ (或 \geqslant)\) ,且 \(\lim{x_n}=\lim{z_n}=a\) ,则 \(\lim{y_n}=a\)
以及下面的运算法则:
对于序列 \(x_n\) ,\(y_n\) ,若 \(\lim{x_n}=a\) , \(\lim{y_n}=b\) , 则:
\((ⅰ)\quad\) \(\lim{(x_n \pm y_n)}=a \pm b\)
\((ⅱ)\quad\) \(\lim{k \cdot x_n}=ka\) ( \(k\) 为常数,本定理可以看作定理\((ⅰ)\)的推论)
\((ⅲ)\quad\) \(\lim{(x_ny_n)}=ab\)
\((ⅳ)\quad\) \(\lim{\frac{x_n}{y_n}}=\frac{a}{b}\) (此时 \(b \neq 0\) )
这些定理能很好地帮助我们解决有关极限的诸多问题。
但是,上述定理对两个无穷大的差、两个无穷大的比、两个无穷小的比以及无穷大和无穷小的积,即:
的值如何计算,这些定理并没有给出答案。它们被称为不定式,对它们的研究被称为不定式的定值法。
—2.例题
下面是一些求极限的例题:
-
一个非常简单的极限
对于序列 \(x_n=\frac{n-1}{n+1}\) ,求 \(\lim{x_n}\) 的值
\[x_n=\frac{n-1}{n+1}=1+\frac{2}{n+1} \]令 \(x^{'}_n=\frac{1}{n+1}\) 。对于任意正数 \(\epsilon\) ,取正整数 \(N > \frac{1}{\epsilon} -1\) ,则对于任意 \(n>N\) ,有:
\[\lvert x^{'}_n - 0 \rvert = x^{'}_n = \frac{1}{n+1}<\frac{1}{N+1} < \frac{1}{\frac{1}{\epsilon}} = \epsilon \]即 \(\lim{x^{'}_n}=0\) ,那么:
\[\lim{x_n}=\lim\left(1+\frac{2}{n+1}\right)=1+\lim{\frac{2}{n+1}}=1+2\cdot \lim{x^{'}_n}=1 \]这就得到答案 \(\lim{x_n}=1\) 。这里用到了极限的定义和定理 \((ⅰ)(ⅱ)\) 。
-
锥体体积的求法
求如图的三角锥体 \(S-ABC\) 的体积 \(V\),其底面积 \(S_{\triangle{ABC}}=S\) ,高为 \(H\) 。
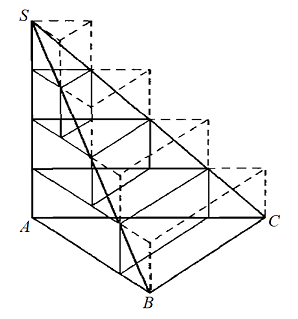
将锥体的高 \(H\) 进行 \(n\) 等分,过各等分点作平行于底面的平面,它们会在锥体上截出一系列与底面相似的三角形,其面积 \(S_k=\frac{k^2}{n^2}S\quad(k=1,2,\dotsi,n-1)\) 。以这些三角形(包括底面)作一系列内含与外包的柱体,则外包的柱体的体积之和 \(V_n\) 与内含的柱体的体积之和 \(V_{n}^{'}\) 满足:
\[V_n=\sum_{k=1}^{n}{\frac{k^2H}{n^3}S} > V > V_{n}^{'}=\sum_{k=0}^{n-1}{\frac{k^2H}{n^3}S} \]但当 \(n\) 增大时,有:
\[V_n-V_{n}^{'}=\frac{H}{n}S \to 0 \ , \quad 即\ \lim{V_n}=\lim{V_{n}^{'}} \quad (根据上面的定理(ⅰ)) \]所以根据上面的定理 \((Ⅲ)\) ,有:
\[V=\lim{V_n}=\lim{V_{n}^{'}} \]因此可通过求 \(\lim{V_n}\) 求得 \(V\) :
\[\begin{align*} V=\lim{V_n} & =\lim{\sum_{k=1}^{n}{\frac{k^2H}{n^3}S}} \\ & =\lim{\frac{HS}{n^3}\sum_{k=1}^{n}{k^2}}\\ & =HS\cdot\lim{\frac{n(n+1)(2n+1)}{6n^3}}\\ & =HS\cdot\lim{\left(\frac{1}{3}+\frac{1}{2n}+\frac{1}{6n^2}\right)}=\frac{HS}{3} \end{align*} \]这里用到了定理 \((ⅰ)(ⅱ)\) ,以及前 \(n\) 个自然数的平方和公式。以上的证明过程可以推广到任意底面形状的锥体。
-
一个简单但著名的问题
证明: \(0.\dot{9}=1\)
构造序列
\[x_n = 0.\underbrace{999 \dotsm 9}_{n个9} = 1-\frac{1}{10^n}\\ \]并定义 \(0.\dot{9}=\lim{x_n}\) 。对于任意正数 \(\epsilon\) ,取正整数 \(N > \log_{10}{\frac{1}{\epsilon}}\) ,则对于任意 \(n>N\) ,有:
\[\lvert x_n -1 \rvert=\frac{1}{10^n}<\frac{1}{10^N} <\frac{1}{10^{\log_{10}{\frac{1}{\epsilon}}}} =\frac{1}{\frac{1}{\epsilon}}=\epsilon \]即 \(\lim{x_n}=1\) ,所以:
\[0.\dot{9}=\lim{x_n}=1 \]命题证明完毕。
§3.函数的极限
—1.定义及定理
函数,描述了两个变量——自变量 \(x\) 和因变量 \(y\) ——之间的一种对应关系。我们既然定义了序列(可以视作一个变量)的极限,便很自然引出函数的的极限的定义:
对于任意正数 \(\epsilon\) ,存在一个正数 \(\delta\) ,使得
\[若 \ \lvert x-a \rvert < \delta \\ 则 \ \lvert f(x)-A \rvert < \epsilon \]则称当 \(x\) 趋于 \(a\) 时函数 \(f(x)\) 的极限为 \(A\) ,记作
\[\lim_{x \to a}{f(x)}=A \]
由于这定义的格式太过于经典,也被称为“ \(\epsilon-\delta\) 语言”。这两个希腊字母 \(\epsilon(epsilon)\) 和 \(\delta(delta)\) [4]在以后的章节还会是我们的常客。
其实,序列 \(x_n\) 可以看作是以 \(n\) 为自变量,定义域为正整数集合( \(n \in \mathbb{N}\) )的函数 \(x(n)\) ;序列 \(x_n\) 的极限 \(\lim{x_n}\) 就相当于函数 \(x(n)\) 的极限 \(\lim_{n \to \infin}{x(n)}\) 。函数的极限源于(至少在思想源头上相同)序列的极限,反过来又包含了序列的极限,是数学上极其典型的“父子关系”。
这里并没有给出如同序列的极限中的 \((4)(5)(6)\) 的式子的定义,即当 \(x>\Delta\) (或 \(<-\Delta\) ),以及 \(f(x)>\Epsilon\) (或 \(<-\Epsilon\) )时,函数极限的定义。我们可以仿照序列的定义写作 \(\lim_{x \to a}{f(x)}=\infin\) (当 \(\lvert x-a \rvert < \delta\) 时,满足 \(f(x) > \Epsilon\) )。其余情况请试着自己写出。
十分自然的,函数的极限”继承“了序列的极限的所有性质(如果要严格证明的话,其方法也与序列的极限的性质的证明方法类似),只不过多了一个前提条件:
对于函数 \(f(x)\) ,\(g(x)\) ,\(h(x)\) ,在充分小的邻域[5] \((a-\epsilon,a+\epsilon)\) 中(这里实际上默认了函数在这一区间里的每一点都有定义):
\((Ⅰ)\quad\) 若总有 \(f(x)=g(x)\) ,则 \(\lim_{x \to a}{f(x)}=\lim_{x \to a}{g(x)}\)
\((Ⅱ)\quad\) 若总有 \(f(x)>g(x) \ (或 \geqslant)\) ,则 \(\lim_{x \to a}{f(x)} \geqslant \lim_{x \to a}{g(x)}\) (反之亦然)
\((Ⅲ)\quad\) 夹逼定理:若总有 \(f(x) > g(x) > h(x) \ (或 \geqslant)\) ,且 \(\lim_{x \to a}{f(x)}=\lim_{x \to a}{h(x)}=A\)
,则 \(\lim_{x \to a}{g(x)}=A\)若 \(\lim_{x \to a}{f(x)}=A\) , \(\lim_{x \to a}{g(x)}=B\) ,则:
\((ⅰ)\quad\) \(\lim_{x \to a}{(f(x) \pm g(x))}=A \pm B\)
\((ⅱ)\quad\) \(\lim_{x \to a}{k \cdot f(x)}=kA\) ( \(k\) 为常数)
\((ⅲ)\quad\) \(\lim_{x \to a}{(f(x)g(x))}=A \cdot B\)
\((ⅳ)\quad\) \(\lim_{x \to a}{\frac{f(x)}{g(x)}}=\frac{A}{B}\) (此时 \(B \neq 0\) )
—2.一些简单的函数极限
-
有理整函数
证明:对于关于 \(x\) 的整式 \(f(x)=a_0+a_1x^1+a_2x^2\dotsm+a_nx^n\) (其中 \(n\) 为自然数,\(a_0,a_1,a_2,\dotsm,a_n\) 为常数 ),函数 \(y=f(x)\) 的极限满足 \(\lim_{x \to k}{f(x)}=f(k)\) 。
我们将 \(f(x)\) 分拆成如下 \(n\) 个函数的和:
\[\begin{align*} & f_0(x)=x^0=1,f_1(x)=x^1=x,f_2(x)=x^2,\dotsm,f_n(x)=x^n \\ & f(x)=a_0 \cdot f_0(x)+a_1 \cdot f_1(x)+a_2 \cdot f_2(x) +\dotsm+a_n \cdot f_n(x) \end{align*} \]考虑其中任意一个函数 \(f_i(x)=x^i\) ,对于任意正数 \(\epsilon\) ,存在一个正数 \(\delta=\sqrt[i]{\epsilon+k^i}-k\) ,使得当 \(0<x-k<\delta\) 时,有 \(k<x<\delta+k=\sqrt[i]{\epsilon+k^i}\) ,且:
\[\begin{align*} f_i(x)-f_i(k) & =x^i-k^i\\ & <\left(\sqrt[i]{\epsilon+k^i}\right)^i-k^i\\ & =\epsilon+k^i-k^i\\ & =\epsilon \end{align*} \]即 \(\lim_{x \to k}{f_i(x)}=f_i(k)\) ,那么:
\[\begin{align*} \lim_{x \to k}{f(x)} & =\lim_{x \to k}{(a_0 \cdot f_0(x)+a_1 \cdot f_1(x)+a_2 \cdot f_2(x)+\dotsm+a_n \cdot f_n(x))}\\ & =\lim_{x \to k}{a_0 \cdot f_0(x)}+\lim_{x \to k}{a_1 \cdot f_1(x)}+\lim_{x \to k}{a_2 \cdot f_2(x)}+\dotsm+\lim_{x \to k}{a_n \cdot f_n(x)} \\ & =a_0 \cdot \lim_{x \to k}{f_0(x)}+a_1 \cdot \lim_{x \to k}{f_1(x)}+a_2 \cdot \lim_{x \to k}{f_2(x)}+ \cdots +a_n \cdot \lim_{x \to k}{f_n(x)} \\ & =a_0 \cdot f_0(k)+a_1 \cdot f_1(k)+a_2 \cdot f_2(k)+\dotsm+a_n \cdot f_n(k)\\ & =f(k) \end{align*} \]即 \(\lim_{x \to k}{f(x)}=f(k)\) ,命题证明完毕。这里用到了极限的定义和定理 \((ⅰ)(ⅱ)\) 。
附注:
我们把满足 \(\lim_{x \to a}{f(x)}=f(a)\) 的函数 \(f(x)\) 称为在点 \(a\) 处连续。连续的函数会有一些很好的性质。所有的初等函数在它有定义的点都是连续的。 -
有理分式函数[6]
对于上文中的 \(f(x)\) 以及关于 \(x\) 的整式 \(g(x)=b_0+b_1x^1+b_2x^2\dotsm+b_mx^m\) (其中 \(m\) 为自然数,\(b_0,b_1,b_2,\dotsm,b_m\) 为常数 ),函数 \(y=\frac{f(x)}{g(x)}\) 在 \(0\) 与 \(\pm \infin\) 处的极限有:
\[\lim_{x \to 0}y=\left\{ \begin{align*} & 0 && (a_0=0) \\ & \frac{a_0}{b_0} && (a_0\neq0,b_0\neq0) \\ & DNE && (b_0=0) \end{align*} \right. \quad,\quad \lim_{x \to \pm \infin}y=\left\{ \begin{aligned} & 0 && (m>n) \\ & \frac{a_0}{b_0} && (m=n) \\ & \pm \infin && (m<n) \end{aligned} \right. \]而在 \(g(x)\) 的零点 \(a\) 处的极限有:
\[\lim_{x \to a}y=\left\{ \begin{align*} & \lim_{x \to a}{\frac{\phi(a)}{\psi(a)}} && (f(x)=(x-a)\phi(x),g(x)=(x-a)\psi(x)) \\ & DNE && (f(a)\neq0) \end{align*} \right. \]读者不妨用极限的定理 \((ⅳ)\) 加以证明。
-
三角函数[7]的极限
-
$ \cos x $
证明: \(\displaystyle{\lim_{x \to 0}{\cos x}=1}\)
对于任意正数 \(\epsilon\) ,存在一正数 \(\delta\) 满足 \(0<\sin\frac{\delta}{2}<\frac{\epsilon}{2}\) ,使得当 \(\lvert x \rvert < \delta\) 时:
\[1-\cos x=\cos0-\cos x = 2\sin^2\frac{x}{2} < 2\sin^2\frac{\delta}{2} < 2\sin\frac{\delta}{2} < \epsilon \]即 \(\lim_{x \to 0}{\cos x}=1\) ,命题证明完毕。这里用到了和差化积[8]和极限的定义。
-
\(\sin x\)
比起 \(\sin x\) 本身的极限(根据诱导公式 \(\sin x=\cos(x-\frac{\pi}{2})\) 可以简单地导出),我们更关心的是以下这个十分重要的极限:
证明: \(\displaystyle{\lim_{x\to0}{\frac{\sin}{x}}=1}\)首先证明如下的重要关系式:
\[\sin x<x<\tan x \qquad (0<x<\frac{\pi}{2}) \]取半径为 \(R\) 的 \(\odot O\) 中的 \(\angle AOB =x\) ,作 \(\odot O\) 在 \(A\) 点的切线 \(AC\) 交 \(OB\) 于点 \(C\) ,如下图:
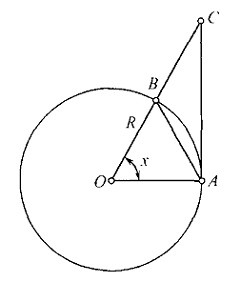
那么由图可知:
\[S_{\triangle AOB}=\frac{1}{2}R^2\sin x < S_{\text{扇形}AOB}=\frac{1}{2}R^2x < S_{\triangle AOC}=\frac{1}{2}R^2\tan x \]各式同时除以 \(\frac{1}{2}R^2\) 就得到关系式 \(\sin x<x<\tan x\) 。
两边同时除以 \(\sin x\) 再取倒数,就得到:
\[1>\frac{\sin x}{x}>\cos x \]又 \(\displaystyle{\lim_{x \to 0}{\cos x}=1}\) ,所以 \(\displaystyle{\lim_{x\to0}{\frac{\sin}{x}}=1}\) ,命题证明完毕。这里用到了 \(\cos x\) 的极限和定理 \((Ⅲ)\) 。
附注:
我们把满足 \(\lim_{x \to a}{\frac{f(x)}{g(x)}}=1\) 的两函数 \(f(x)\) 、 \(g(x)\) 称为“当 \(x \to a\) 时 \(f(x) \sim g(x)\) ”。满足这样关系的函数可以在当 \(x \to a\) 时相互替换而不改变式子的值。这样的关系能在很多时候把复杂的函数替换成简单的函数。
其余的三角函数皆可用上面的两个三角函数表示。
-
§4.极限的实操
—1.数 \(e\) 的定义
考察这样一个序列:
使用二项式定理,我们发现:
比较 \(x_n\) 与 \(x_{n+1}\) 的大小,有:
即 \(x_n<x_{n+1}\) ,这个序列单调递增。将所有的 \(\left( 1 - \frac{i}{n} \right)\) 换成 \(1\) ,又有:
这个序列有上界。一个单调递增又有上界的序列,显然有一有限极限[9]。我们把这一极限极限记作:
数 \(e\) 本身应用广泛,以它为底的对数函数( \(y=\log_{e}x=\ln x\) ,这被称为自然对数)和指数函数( \(y=e^x\) )有很多优美的性质,我们在以后的章节会常常见到它们。
那么从序列拓展到函数,我们有如下的命题:
证明: \(\displaystyle{\lim_{x \to \pm \infin}{\left( 1 + \frac{1}{x} \right)^x}=e}\)
首先考虑 \(x \to +\infin\) 的情况。对于任意大的 \(x\) ,取正整数 \(n\) 满足 \(n_x \leqslant x < n_x+1\) ,则当 \(x \to +\infin\) 时,有 \(n_x \to +\infin\) 。这时:
\[\frac{1}{n_x+1} < \frac{1}{x} \leqslant \frac{1}{n_x} \\ 1+\frac{1}{n_x+1} < 1+\frac{1}{x} \leqslant 1+\frac{1}{n_x} \\ {\left( 1+\frac{1}{n_x+1} \right)}^{n_x} < {\left( 1+\frac{1}{x} \right)}^x \leqslant {\left( 1+\frac{1}{n_x} \right)}^{n_x+1} \\ \]两边的式子的极限为:
\[\begin{align*} & \lim{{\left( 1+\frac{1}{n_x+1} \right)}^{n_x}} = \cfrac{\lim{{\left( 1+\cfrac{1}{n_x+1} \right)}^{n_x+1}}}{\lim{\left( 1+\cfrac{1}{n_x+1} \right)}} = e \\ & \lim{{\left( 1+\frac{1}{n_x} \right)}^{n_x+1}} = \lim{{\left( 1+\cfrac{1}{n_x} \right)}^{n_x}}\cdot\lim{\left( 1+\cfrac{1}{n_x} \right)} = e \end{align*} \]所以有 \(\displaystyle{\lim_{x \to +\infin}{\left( 1 + \frac{1}{x} \right)^x}=e}\) 。 \(x \to -\infin\) 的情况只需换元 \(t=-x\) ,就有:
\[\begin{align*} \lim_{x \to -\infin}{\left( 1 + \frac{1}{x} \right)^x} & = \lim_{t \to +\infin}{\left( 1 - \frac{1}{t} \right)^{-t}} \\ & = \lim_{t \to +\infin}{\left( \frac{t}{t-1} \right)^t} \\ & = \lim_{t \to +\infin}{\left( 1 + \frac{1}{t-1} \right)^{t-1}} \cdot \lim_{t \to +\infin}{\left( 1 + \frac{1}{t-1} \right)} \\ & = e \end{align*} \]命题证明完毕。这里用到了 \(e\) 的定义和定理 \((Ⅲ)\) 。定理的等价表述是 \(\lim_{x \to 0}{( 1 + x )^{\frac{1}{x}}}=e\) 。
—2.圆的周长面积公式的验证
相信你早在小学就学过圆的周长面积公式,但并没有严谨地证明(或者说验证)它们。我们不妨从极限论的角度验证这个公式,顺便练习三角函数的极限。
我们知道对于顶角为 \(\theta\) 、腰长为 \(r\) 的等腰三角形,其底边长度为 \(2r\cdot\sin{\frac{\theta}{2}}\) ,其面积为 \(\frac{1}{2}r^2\cdot\sin{\theta}\) ;不妨用正 \(n\) 边形去逼近圆(相当于把圆视作正 \(\infin\) 边形,动态演示见文件 §4-2.ggb ),那么有:
就得到圆的周长与面积公式。这里用到了 \(\sin x\) 的极限(只需注意到 \(\frac{\pi}{n} \to 0\) , \(\sin{\frac{\pi}{n}} \sim \frac{\pi}{n}\) 即可)。
—3.一个伪证:\(\pi=4\)
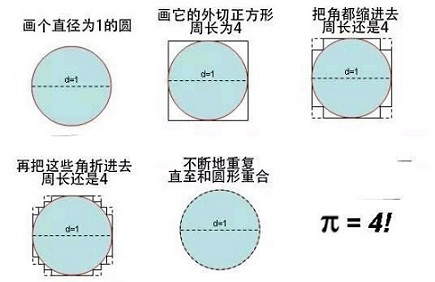
这个伪证尽管看起来十分“合理”,但显然是不正确的。那它错在哪里呢?
若要证 \(\pi=4\) ,不妨从证 \(4-\pi=0\) 下手。从极限论的角度,我们便要构造一个序列 \(x_n\) 逼近(几何意义上) \(4-\pi\) ,并尝试证明 \(\lim{x_n}=0\) 。
根据上图中的“证明”,第 \(n\) 次把角折进去前,每一个角和这一个角所“夹住”的圆弧从差为 \(\delta_n=\frac{4-\pi}{4n}\) ,显然有 \(\lim{\delta_n}=0\) ,每一份的差的确趋于 \(0\) 。但总体的差 \(x_n=4n\cdot\delta_n=4-\pi\) 为常数,并不能说明 \(4-\pi=\lim{x_n}\) (这一个极限是由几何图形得来的)等于 \(0\) 。这里的 \(x_n\) 其实是一个 \(0\cdot\infin\) 型不等式,仅仅针对其中趋于 \(0\) 的一部分,就说整体趋于 \(0\) ,是错误的。
华罗庚老先生说过“形少数时难入微”。在面对无穷小、无穷大这样的对象时,图形的表现往往差强人意。从极限论(乃至微积分学)的角度看,图形的作用仅在于启发思路或直观定性,真正的结论还是要从计算中得出。
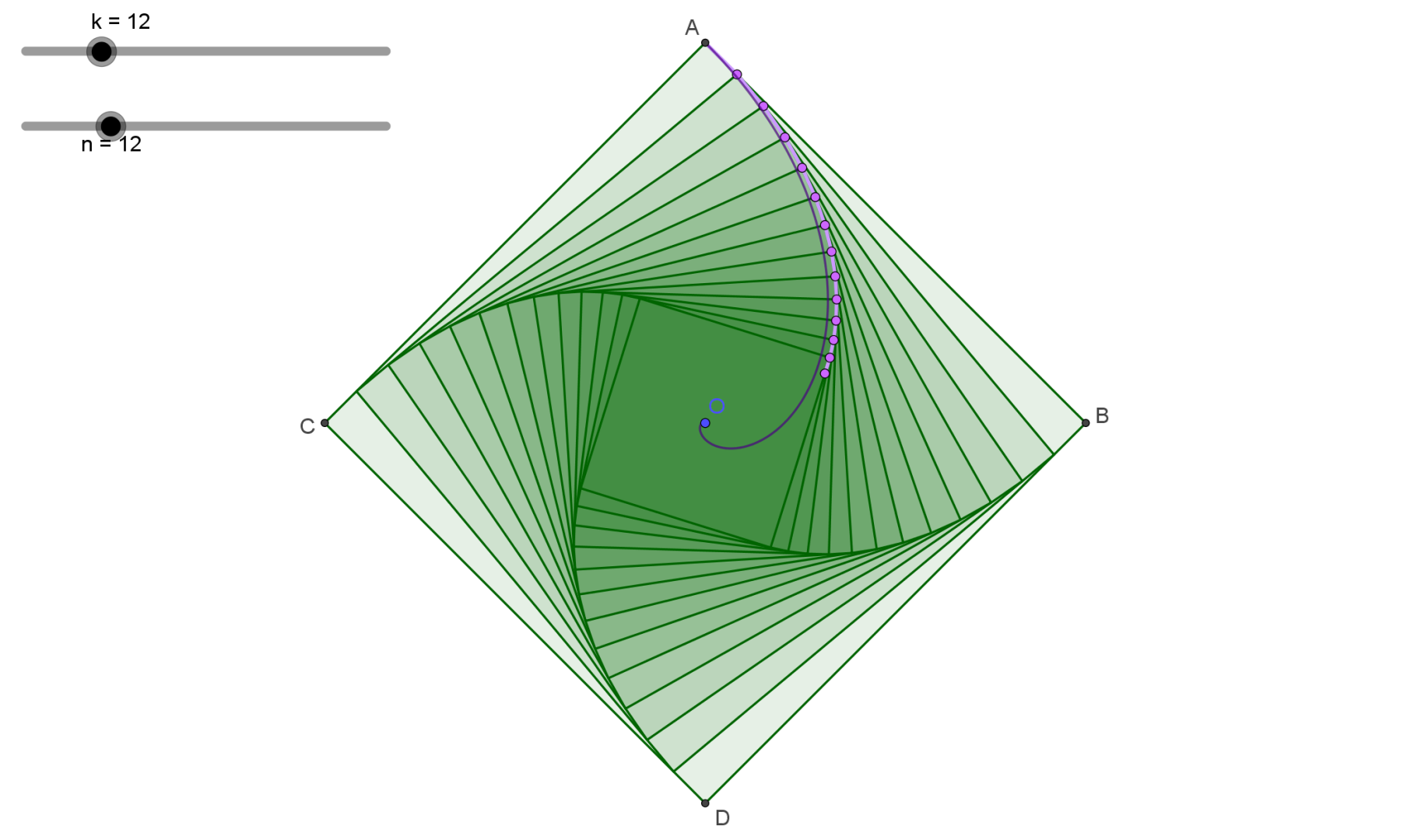
—4.正方形上的蜗牛
下面一道趣题,可以看作本篇的结束。
在一个边长为 \(l\) 的正方形的四个顶点上有四只蜗牛,每只蜗牛以相同速度匀速向它顺时针方向的那一只蜗牛爬去,蜗牛在爬动过程中会不断调整爬动方向,使之正对着它要爬向的蜗牛。求四只蜗牛相遇于正方形中心所要经过的距离。
为了方便处理“连续的”转向,我们不妨假设,每只蜗牛爬了与目标蜗牛当前距离的 \(\frac{1}{k} \ (k>2)\) 时才意识到自己要转向; 注意到蜗牛在相遇于正方形中心前需要无数次转向(这也是我们无法处理的),不妨假设蜗牛转向了 \(n\) 次之后就停止;如下图(紫色的曲线是蜗牛的实际路径,紫红色点是假设中蜗牛的转向处,粉红色的折线是假设中蜗牛走过的路径。动态演示见文件 §4-4.ggb ):
用式子把假设中路径的长度 \(L_n(k)\) 表示出来,并对 \(n\) 作序列 \(L_n(k)\) 的极限,得到无数次旋转后的路径长度关于 \(k\) 的函数 \(L(k)=\lim{L_n(k)}\) ;要使蜗牛的“延时” \(\frac{1}{k} \to 0\) ,就要再对 \(k\to\infin\) 作函数 \(L(k)\) 的极限,即可求出答案 \(L=\lim_{k\to\infin}{L(k)}\) 。
注意到四只蜗牛同批次转向点构成的正方形等比相似,相邻两次的相似比为 \(\cfrac{\sqrt{(k-1)^2+1}}{k}\) (由勾股定理得出,相似比 \(<1\) );则第 \(i\) 个正方形的边长为 \(l \cdot \left( \cfrac{\sqrt{(k-1)^2+1}}{k} \right)^i\) ,而第 \(i\) 段线段的长度是边长的 \(\cfrac{1}{k}\) ,即 \(\cfrac{l}{k} \cdot \left( \cfrac{\sqrt{(k-1)^2+1}}{k} \right)^i\) ;对这些线段求和,得到:
\[\begin{align*} L_{n}(k) & =\sum_{i=0}^{n}{\left( \frac{l}{k} \cdot \left( \frac{\sqrt{(k-1)^2+1}}{k} \right)^i \right)} \\ & =\frac{l}{k} \cdot \frac{1 - \left( \cfrac{\sqrt{(k-1)^2+1}}{k} \right)^{n+1}}{1-\cfrac{\sqrt{(k-1)^2+1}}{k}} \\ & =\frac{l}{k} \cdot \left( 1 - \left( \frac{\sqrt{(k-1)^2+1}}{k} \right)^{n+1} \right) \cdot \frac{k}{k-\sqrt{(k-1)^2+1}} \end{align*} \]这里用到了等比数列的计算公式[10]。对以上式子对 \(n\) 作序列的极限(把 \(k\) 视作常数),得到:
\[\begin{align*} L(k) & =\lim{L_{n}(k)} \\ & =\frac{l}{k} \cdot \frac{k}{k-\sqrt{(k-1)^2+1}} \cdot \lim{\left( 1 - \left( \frac{\sqrt{(k-1)^2+1}}{k} \right)^{n+1} \right)} \\ & =\frac{l}{k-\sqrt{(k-1)^2+1}} \end{align*} \]后一项的极限 \(0\) 是容易得到的。对以上式子对 \(k\to\infin\) 作函数的极限,得到:
\[L=\lim_{k\to\infin}{L(k)}=l \cdot \lim_{k\to\infin}{\frac{1}{k-\sqrt{(k-1)^2+1}}} \]注意到当 \(k\to\infin\) 时,有 \(\sqrt{(k-1)^2+1} \sim (k-1)\) (感性地理解: \(+1\) 面对 \((k-1)^2 \to \infin\) 是可以忽略的),把这带入以上式子,得到一个及其美妙的结果:
\[L=\lim_{k\to\infin}{L(k)}=l \]附注1:
蜗牛爬过的曲线其实是对数螺线 \(r=A \cdot e^{\theta}\) (其中 \(A\) 为常数,作用为缩放函数图像,它与正方形边长 \(l\) 的具体关系是 \(l=\sqrt{2}e^{\pi/2} \cdot A\) ),这条螺线的一些性质会在后面的章节加以研究。附注2:
此题其实另有一个取巧的思路:考虑到蜗牛两两之间垂直方向上的初始距离为正方形边长 \(l\) ;由于连续的转向运动,蜗牛的运动方向始终两两垂直,即垂直方向上的相对速度差为 \(0\) ,就可以视目标蜗牛在垂直方向上静止;那么要爬向距离为 \(l\) 的静止物体要经过的距离就是 \(l\) 。
极限论的内容就是这么多。它不仅是整个微积分(标准分析)的理论基础,也是思想基础。这种近乎暴力的“用有限逼近无穷,用离散逼近连续”的方法,就是微积分这种“数学方法”的本质所在。微积分的大门已在你面前敞开,我们即将跟随牛老爵爷的步伐走进微分的世界。欲知后事如何,且看下章。
证明如下:假设存在正数 \(a\) (负数同理),使得任意正数 \(n\) 都有 \(n>a>0\) ,则根据实数的稠密性,必存在一个正数 \(b\) 满足 \(a>b>0\) ,假设不成立。即不存在这样的正数 \(a\) 。 ↩︎
1734年,大主教乔治·贝克莱以“渺小的哲学家”之名出版了一本标题很长的书《分析学家:或一篇致一位不信神数学家的论文,其中审查一下近代分析学的对象、原则及论断是不是比宗教的神秘、信仰的要点有更清晰的表达,或更明显的推理》。在这本书中,贝克莱对当时的分析理论进行了攻击。因为无穷小量在当时的分析理论中一会儿说是零,一会儿又说不是零。因此,贝克莱嘲笑无穷小量是“已死量的幽灵”。 ↩︎
证明如下:根据条件和极限的定义,对于任意正数 \(\epsilon\) ,存在一个正整数 \(N\) ,使在 \(n>N\) 时,一切 \(x_n,z_n\) 的值满足 \(a+\epsilon>x_n>z_n>a-\epsilon\) ,又有 \(x_n>y_n>z_n\),则 \(a+\epsilon>y_n>a-\epsilon\) ,即 \(\lim{y_n}=a\) 。 ↩︎
在《美丽新世界》中,“delta“、“epsilon”分别指第四、第五等公民。 ↩︎
对于点 \(a\) 与正数 \(\delta\) ,开区间 \((a-\delta,a+\delta)\) 即为中心为点 \(a\) 、半径为 \(\delta\) 的一个邻域。绝大多数情况下,除去邻域中的点 \(a\) (即只考虑区间 \((a-\delta,a)\cup(a,a+\delta)\) )不会影响讨论的普遍性。 ↩︎
下文中的“DNE”即“不存在(Do Not Exist)”的缩写。极限存在性的具体条件会在本章的附加章节里详细讨论。 ↩︎
如果没有特别说明,一切三角函数的自变量(乃至一切角度)都采用弧度制,这样做的好处会在涉及三角函数的极限中充分体现。 ↩︎
\(\cos \alpha - \cos \beta=-2\sin\frac{\alpha-\beta}{2}\sin\frac{\alpha+\beta}{2}\) ↩︎
这里不妨考虑单调递增但有上界的序列 \(x_n\) 。根据“上确界原理”,存在实数 \(m=\sup\{x_n\}\) ;根据上确界的性质,对于任意正数 \(\epsilon\) ,存在 \(m-x_N<\epsilon\) ;又由单调性,对于任意 \(n>N\) ,有 \(x_n>x_N\) ,则有 \(m-x_n<\epsilon\) 。这就满足极限的定义,有 \(m=\lim{x_n}\) 。 ↩︎
即 \(\displaystyle{\sum_{i=0}^{n}{a^i}=\frac{1-a^{i+1}}{1-a}\quad(0<a<1)}\) ↩︎


 浙公网安备 33010602011771号
浙公网安备 33010602011771号