各种图论知识
1.floodfill
思路:复制全图,把要填充的部分用边界包起来。每次以BFS的方式,由最靠内的边界向里面扩展,扩展的同时缩小边界。
由“木桶原理”,一个块的水位高度取决于它周围最低的块。所以用一个以高度为标准的小根堆维护准备进行扩展的一圈块,扩展的同时更新最大值,注意最后要减去原来的高度。
整个算法的主体其实就是一个BFS。
2.图论与差分约束
典例1:求一个满足:$N_a-N_b<=k_1,N_b-N_c>k_2...N_x-N_y<=k_n$的长度为$L$的序列($k,L∈Z$)
把不等式变形一下,变成$N_x?N_y+k_n$这个样子(等于可以通过加/减$1$消去),比如$N_3-N_2>=4$等价于$N_3>=N_2+4$,对于$N_x-N_y>=k_n$,从$y$到$x$连一条$val=k_n$的边,然后跑最长路。注意要加一个超级源点跑,不然图可能不连通,这是超级源点的第一个作用;另一个作用是它可以限制每个点的最小值,最小值是多少就连多少的边
序列就是最后的$dis(1)->dis(n)$,注意有负环时无解
典例2:给出一些$(l,r)$至多/少有多少个物品的限制,让你求最多/少有多少物品
转换成前缀和,就变成了上面的问题,$(l,r)$最少有$x$个物品就是$fsum[r]-fsum[l-1]>=x$,此时从$l-1$向$r$连一条$x$的边;同理,最多有$x$个就是连$-x$的边。这里说另一种限制限制方法,就是对于每个位置$i$向$i+1$连一条零边,强行限制前缀和不减少,然后从零号点开始跑最长路即可。
3.矩阵树定理(Matrix_tree 定理)
图$G$的所有不同的生成树的个数等于其基尔霍夫矩阵的任何一个$n-1$阶主子式(也就是删掉一行一列之后得到的一个小矩阵,我们称这个小矩阵为“伴随矩阵”)的行列式绝对值。
其中基尔霍夫矩阵=度数矩阵-邻接矩阵。而$G$的度数矩阵$D[G]$是一个$n*n$的矩阵。当$i!=j$时,$D[i][j]=0$;当$i==j$时,$D[i][j]$等于$i$的度数。
注意矩阵树定理求出来的这个东西是有实际意义的,它是“所有生成树边权乘积之和”(度数矩阵是点的边权和,邻接矩阵是边权)
原理是什么呢?(这里转自@Candy?)
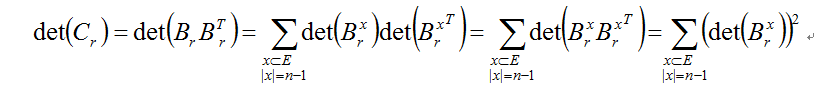
这里$C_r$表示基尔霍夫矩阵,$B_r$表示基尔霍夫矩阵的伴随矩阵
基尔霍夫矩阵的伴随矩阵在计数$n−1$条边集时,若边集中存在环就会产生线性组合而导致行列式为零,所以只有在形成生成树后面的$(det(B_r^x))^2$时产生1的贡献
4.一些关于最小生成树的东西
①若$AB$同为图$G$的最小生成树,$A$的边权从小到大为 $val(a_1),val(a_2),val(a_3)...val(a_n)$,$B$的边权从小到大为$val(b_1),val(b_2),val(b_3)...val(b_n)$,则对于任意的$val(a_i)$与$val(b_i)(i∈N^*)$,有$val(a_i)=val(b_i)$。
②由$Kruskal$算法构造的最小生成树,在任意一种以权值分类的边加入构造后,图的连通性相同
③如果在最小生成树$A$中权值为$k$的边有$x$条,则用任意$x$条权值为$k$的边替换$A$中的权值为$k$的边且不产生环的方案都是合法的最小生成树。
5.树上差分
树上差分全部在节点上进行,最终通过从树根开始的一次DFS得到答案
($for:i->son[nde]$ $DFS(son_i),val[nde]+=val[son_i]$)
①链差分:求$n$条链覆盖的边
将各个链的起点$b$与终点$e+1$,$lca(b,e)-2$,所有权值为$n$的节点和它们爸爸间的边即为答案
②点差分:求节点被链覆盖的次数
将各个链的起点$b$与终点$e+1$,$lca(b,e)-1$,$fth[lca(b,e)]-1$,每个节点的权值即为自己的答案
7.平面图判定
平面图的边数$m$小于等于$3*n-6$,其中$n$为图的点数
8.哈密顿路径/回路
含有图中所有顶点的路径称作哈密顿路径,闭合的哈密顿路径称作哈密顿回路。
9.最大团
一张图的最大团等于其补图的最大独立集
10.判断某条边$e(u,v)$是否在$s->t$的最短路上
$dis[s][u]+val[e]+dis[v][t]==dis[s][t]$
11.最小链覆盖与最长反链
它们首先都是DAG上的概念
最小链覆盖:字面意思,用最少的链覆盖所有点的链数
最长反链:一个点的集合,其中的点两两不可达
Dilworth定理告诉我们:最长反链=最小链覆盖
最长链=最小反链覆盖
12.树的重心
一些性质:
性质 0 (显然):一棵树有最多两个重心。
性质 1 :树中所有点到重心的距离和是最小的。
性质 2 :把两棵树通过加一条边得到一颗新的树,新的树的重心必然在连接原来两棵树重心的路径上。
性质 3 :一棵树添加或者删除一个节点,树的重心最多只移动一条边的位置。
13.欧拉(回)路
寻找欧拉回路时从度数最小的点开始,寻找普通的欧拉路时从度数最小的奇节点开始
14.树上链交
一条链的LCA在另一条链上
15.Prufer序列
树->Prufer序列
迭代删点直到原图仅剩两个点。第$i$次删掉标号最小的叶子之后把第$i$项设为该叶子邻接点的标号
Prufer序列->树
还原一棵$n$个节点的树:设集合$S={1,2...n-1,n}$,找到集合中最小的未在集合中出现的数$x$,将$x$与序列首项连接,然后在集合中删除$x$并删掉Prufer序列的首项。最后把剩下的两个点连起来
n个点形成的k个联通块的生成树个数:$n^{n-k-2}\prod\limits_{i=1}^k siz[i]$
prufer序列中每个节点的编号出现了其度数减一次,因此给定每个节点的度数时无根树数目即为$\frac{(n-2)!}{\prod (deg-1)}$
可以拿来和生成函数那一套一起搞
16.网络流平面图转对偶图
在原来的起点和终点间连一条边,边的两侧就是新的源汇点
17.n个点带标号的哈密顿回路总数
$(n-1)*2^{\frac{n(n-1)}{2}-n}$,其中$n>=3$($n=2$时没有,$n=1$时有1个)
就是先搞出来一个n的排列把它连成环,然后这样环里的每条边在每个环里都被算了一次,所以除掉n,然后剩下的$\frac{n(n-1)}{2}-n$条边随便连
18.三元环计数
19.霍尔定理
二分图有完美匹配当且当任意k个左部点都有至少任意k个右部点与它们相邻


 浙公网安备 33010602011771号
浙公网安备 33010602011771号