各种数学知识2

Update on 2019.3.21

 

1.错排问题

$D(1)=0,D(2)=1,D(n)=(n-1)*(D(n-1)+D(n-2))$ $(n>=3\&\& n∈N^*)$

2.组合恒等式(感觉没啥用)

①$C_n^i=C_n^{n-i}$ ②$kC_n^k=nC_{n-1}^{k-1}$ ③$C_n^m=C_{n-1}^m+C_{n-1}^{m-1}$ ④$\frac{1}{k+1}C_n^k=\frac{1}{n+1}C_{n+1}^{k+1}$

⑤$\sum \limits _{i=0}^{n}$ $C_n^i=2^n$ ⑥$C_n^mC_m^k=C_n^kC_{n-k}^{m-k}$ ⑦$\sum \limits _{i=m}^{n}C_i^m=C_{n+1}^{m+1}$ ⑧$\sum \limits$ $C_n^{odd}=$ $\sum \limits$ $C_n^{even}=$ $\frac{1}{2}$ $\sum \limits _{i=0}^{n}$ $C_n^i$ $=2^{n-1}$

⑨$C_{m+n}^k=\sum \limits _{i=0}^{k}C_m^iC_n^{k-i}$ ⑩$\sum\limits_{i=1}^{n}C_{i+m}^m=C_{i+m+1}^{m+1}-1$

更有用的：把杨辉三角打出来，瞪一瞪你想要的规律

3.一个“常见”方法

$a^k=\sum\limits_{i=0}^{k}S_k^iC_a^i*i!$

4.二项式定理

$(a+b)^n=\sum\limits_{i=0}^{n}C_n^ia^ib^{n-i}$

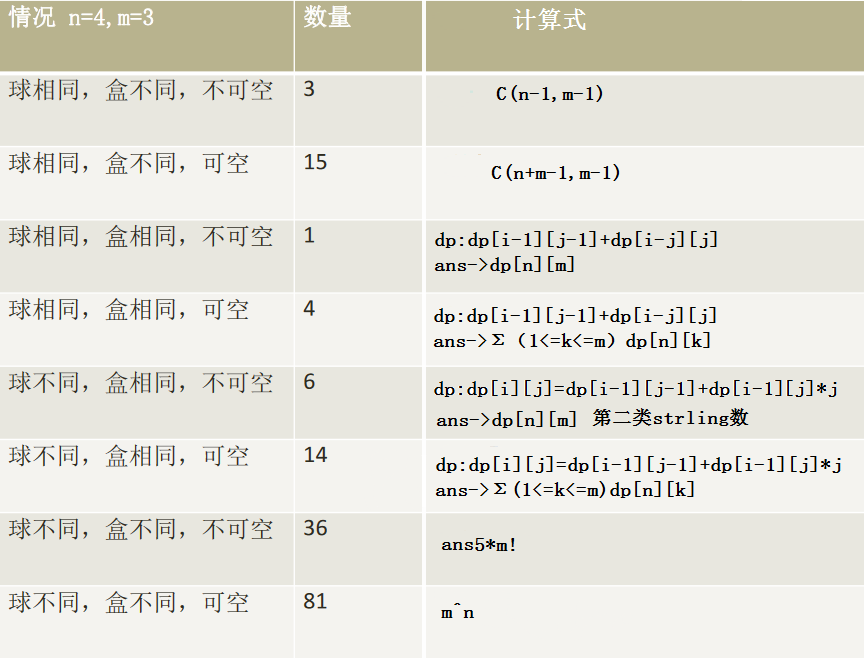
5.乒乓球与盒子的故事— —物品的选取方案

将$n$个乒乓球放入$m$个盒子中，求方案数。可能会出现这些情况：

①乒乓球相同/不同

②盒子相同/不同

③盒子允许空/不允许空

共有8个子问题：

6.$Lucas$定理

$Lucas(n,m,p)=C_{n\%p}^{m\%p}*Lucas(\frac{n}{p},\frac{m}{p},p)$其中$p$为素数

同时对于任意的$k∈N$有$Lucas(k,0,p)=1$

放上那道模板题的代码吧quq

#include<cstdio>
long long A[n],B[n];
long long n,m,mod,T;
long long C(long long n,long long m,long long mod) 
{
    return (m<=n)?A[n]*B[n-m]%mod*B[m]%mod:0;
}
long long Lucas(long long n,long long m,long long mod) 
{
    return m?C(n%mod,m%mod,mod)%mod*Lucas(n/mod,m/mod,mod)%mod:1;
}
int main() 
{
    scanf("%lld",&T);
    A[0]=A[1]=B[0]=B[1]=1;
    while(T--)
    {
        scanf("%lld%lld%lld",&n,&m,&mod);
        for(int i=2;i<=mod;i++) B[i]=-(mod/i)*B[mod%i]%mod;
        for(int i=2;i<=mod;i++) A[i]=A[i-1]*i%mod,B[i]=B[i-1]*B[i]%mod;
        printf("%lld\n",(Lucas(n+m,m,mod)+mod)%mod);
    }
    return 0;
}

7.排序不等式

设有两组数$a_1,a_2,……a_n$和$b_1,b_2,……b_n$，满足$a_1≤a_2≤……≤a_n$,$b_1≤b_2≤……≤b_n$，$c_1,c_2,……c_n$是$b_1,b_2,……b_n$的乱序排列，则有$a_1b_n+a_2b_{n-1}+……+a_nb_1≤a_1c_1+a_2c_2+……+a_nc_n≤a_1b_1+a_2b_2+a_nb_n$,当且仅当$a_1=a_2=……=a_n$或$b_1=b_2=……=b_n$时取等。即：反序和$≤$乱序和$≤$顺序和。

8.$Joesphus$问题

最朴素的解法是：枚举人数->枚举当前开始计数的人->枚举越过的人数($O(n^3)$)，普通的$Joesphus$问题是可以优化到$O(n)$递推的，递推式为$J(n+1)=(J(n)+m)/(n+1),J(1)=0(n∈N^*)$。

 

9.康拓展开

将一个排列展开成一个数，这样一个$x$个元素的排列会被映射到一个不超过$x!$的整数，比起直接“按(十进制)位”压缩不知道高到哪里去了

具体步骤：枚举排列中的每个元素$a_i$，求未出现过的比它小的数的个数$s_i$，最终展开结果为$(\sum\limits_{i=1}^xs_i*(x-i)!)+1$

康托展开的逆运算：把一个数$a$收缩成一个$x$个数的排列

具体步骤：将$a$从高到低除以阶乘(即依次除以$(x-1)!......1!,0!$)，得到商$p_i$和余数$r_i$，排列的第$i$位就是第$p_i+1$个未出现过的数，然后每次对余数$r_i$继续这个过程

long long Expand(long long *a)
{
    cnt=0;
    for(int i=1;i<=n;i++)
    {
        mem=0;
        for(int j=i+1;j<=n;j++)
            if(a[i]>a[j]) mem++;
        cnt+=mem*facs[n-i];
    }
    return cnt+1;
}
void Pack(long long a)
{
    a--,memset(used,0,sizeof used);
    for(int i=1;i<=n;i++)
    {
        cnt=a/facs[n-i],a%=facs[n-i];
        for(int j=1;j<=n;j++)
            if(!used[j]&&!(cnt--)) 
                {mem=j; break;}
        used[mem]=true,perm[i]=mem;
    }
    return ;
}

 

10.组合数的奇偶性

$C_n^m$为奇数当且仅当$m$为$n$一个子集

11.Stirling数

第一类斯特林数

将$n$个数划分成$m$个圆排列的方案数，等价于$m$个循环的长度为$n$的置换个数

$Stl1(n,m)=\sum\limits_{i=1}^nStl1(n-i,m-1)*(i-1)!*C_{n-1}^{i-1}$(求和式)$=Stl1(n-1,m-1)+Stl1(n-1,m)*(n-1)$(递推式)

第二类斯特林数

将$n$个数划分为$m$个非空集合的方案数

$\sum\limits_{i=0}^nStl2(n,i)=Bell_n$(贝尔数)

$Stl2(n,m)=\sum\limits_{i=1}^nStl2(n-i,m-1)*C_{n-1}^{i-1}$(求和式)$=Stl2(n-1,m-1)+Stl2(n-1,m)*m$(递推式)

$=\frac{1}{m!}\sum\limits_{i=0}^m (-1)^i C_m^i (m-i)^n$

两者都可以用卷积快速求

12.Kummer定理

$n,m<=A$时被$p^k$整除的$C_n^m$数量->满足$x+y<=A$且在$p$进制下产生了至少$k$次进位的$(x,y)$对数

13.斯特林反演

若有$f(n)=\sum\limits_{i=1}^nStl1(n,i)g(i)$

则有$g(n)=\sum\limits_{i=1}^n(-1)^{n-i}Stl2(n,i)f(i)$

14.哈夫曼树

其实是 NOI 2015 荷马史诗 的题解不想单独写了

学过就会写，没学过......能写出来就太强了

k叉哈夫曼树，就是一次合并k个，不够就补零